6.3. Методика кореляційно-регресійного аналізу

Кореляційно-регресійний аналіз дозволяє визначити тісноту зв'язку між досліджуваними показниками і пропорційність зміни результативного показника при зміні одного чи декількох факторів. Залежно від кількості досліджуваних ознак розрізняють парну (просту) кореляцію, коли аналізують зв’язок між однією факторною і результативною ознаками і множинну, коли вивчають залежність результативної ознаки від двох і більше факторних ознак.

Головною характеристикою кореляційного зв’язку є лінія регресії. Рівняння лінійної регресії має вигляд: .

Параметри і знаходять, розв’язуючи систему нормальних рівнянь:

де п – кількість одиниць сукупності (тобто заданих пар значень х і у). Розв'язавши цю систему, дістанемо:

Для прикладу розрахуємо параметри рівняння лінійної регресії, що характеризує залежність урожайності від якості ґрунту на 10-ти земельних ділянках (табл. 3).

Підставивши відповідні значення в систему рівнянь, отримаємо: 10 +18,3 =341,2;

18,3 +35,77 =641,17.

Використовуючи вище наведені формули, знайдемо значення параметрів:

Таблиця 4

Дані до регресійного аналізу залежності урожайності зернових у (ц/га) від якості ґрунту х (в балах)

№ ділянки	х	у
1	1,3	26,7	1,69	712,89	34,71	30,32	919,3024
2	2,1	32,5	4,41	1056,25	68,25	36,24	1313,3376
3	1,5	27,9	2,25	778,41	41,85	31,8	1011,24
4	2,4	35,0	5,76	1225,00	84	38,46	1479,1716
5	2,2	32,4	4,84	1049,76	71,28	36,98	1367,5204
6	1,9	33,1	3,61	1095,61	62,89	34,76	1208,2576
7	1,0	30,9	1,00	954,81	30,9	28,1	789,61
8	2,5	50,1	6,25	2510,01	125,25	39,2	1536,64
9	1,4	38,6	1,96	1489,96	54,04	31,06	964,7236
10	2,0	34,0	4,00	1156,00	68	35,5	1260,25
Всього	18,3	341,2	35,77	12028,7	641,17	342,42	11850,052
В середньому	1,83	34,12	3,577	1202,87	64,117	34,242	1185,0052

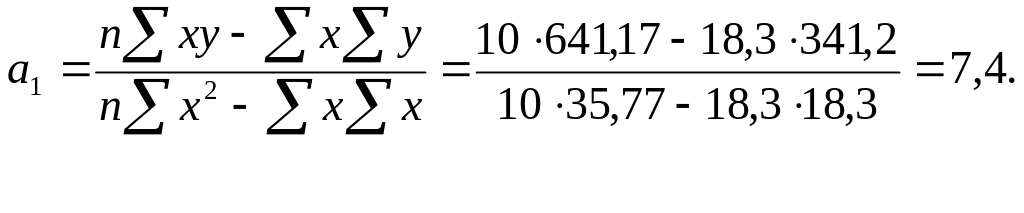
Отже, теоретична залежність рівня урожайності зернових культур від якості ґрунту має такий вигляд:

Це означає, що при збільшенні якості ґрунту на один бал рівень урожайності зростає на 7,4 ц/га.

Для оцінки щільності прямолінійного зв’язку результативної і факторної ознак використовують коефіцієнт парної кореляції, який обчислюють за формулою:

r ₌ ,

де – середнє квадратичне відхилення факторної ознаки; – середнє квадратичне відхилення результативної ознаки.

Так як , а , то формула лінійного коефіцієнта кореляції буде такою:

Розраховане значення коефіцієнта кореляції (r = 0,564) свідчить, що між ознаками іс­нує середня щільність зв'язку.

Тіснота зв'язку в кореляційно-регресійному аналізі вимірюється коефіцієнтом детермінації R². Він дорівнює квадрату коефіцієнта кореляції:

R² = ,

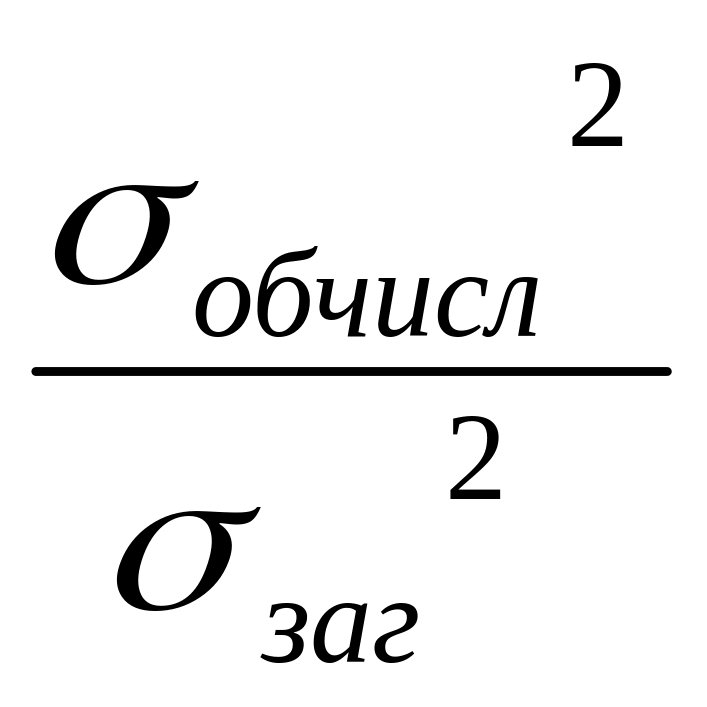де – дисперсія результативного показника, обчислена за рівнянням регресії; – загальна дисперсія результативного показника.

Цей показник пояснює, яка частка варіації досліджуваного показника обумовлюється впливом фактору, включеного до рівняння регресії. Він може мати значення від 0 до 1. Чим ближче коефіцієнт детермінації до одиниці, тим більше варіація результативного показника характеризується впливом досліджуваного фактора.

Так як = , а , то в нашому прикладі = 1185,0052-34,12 =20,8308,

=1202,87-34,12 =38,6956.

Отже, R²= .

В даному випадку коефіцієнт детермінації показує, що урожайність залежить на 53,8% від якості ґрунту і на 46,2% – від інших факторів.

Якщо кількісні показники кореляційного аналізу обчислені за вибірковими даними, то потрібно визначити їх відповідність показникам зв’язку у генеральній сукупності. Середню помилку вибіркового коефіцієнта парної кореляції визначають за такою формулою:

де r – коефіцієнт кореляції, n – вибіркова сукупність.

Вірогідність коефіцієнта кореляції визначають за t-критерієм, який обчислюють як відношення коефіцієнта кореляції до його середньої помилки:

.

Якщо > при встановленому рівні імовірності, то можна зробити висновок, що в генеральній сукупності існує вірогідний зв'язок між досліджуваними ознаками.

У нашому прикладі середня помилка вибіркового коефіцієнта дорівнює .

Фактичне значення t-критерію буде таким:

.

Табличне значення t-критерію при рівні ймовірності 0,95 і 8 ступенях свободи дорівнює 2,3060 (див. додаток В). Оскільки обчислена величина t більше табличної, то можна зробити висновок про вірогідність коефіцієнта кореляції, тобто в даному випадку зв’язок між досліджуваними явищами в генеральній сукупності доведений.