2.4. Метод хорд і метод дотичних
(Загальні питання)
Далі розглянемо методи хорд і дотичних уточнення коренів рівнянь.
Ці
методи відносяться до методів
послідовних наближень
.
Наближення
до кореня знаходяться так: якщо
відомо попередній
наближений
(n=0,
1, 2, ...), то подальше наближення
обчислюється
за формулою
(2.6)
де
Р - деякий вираз, що встановлює
зв'язок між попереднім
і наступним наближеннями.
Починається
процес з будь-якого числа 
з відрізка ізоляції кореня - початкового
принаближення.
Формула виду (2.6) називається рекуррентной формулою, а отриману з її допомогою послідовність наближень називають ітераційної послідовністю
Отже,
нехай дано рівняння (2.1): 
>
=
0, корінь t
якого відділен на відрізку [а; b].
При уточненні кореня обома методами будемо вважати, що значеннями) функції f нa кінцях відрізку мають різні знаки, крім того, функція f має неперервні похідні f ' і f" з відмінними від нуля і зберігающими постійний знак значеннями при всіх x є [a;b].
Для виконання наведених умов іноді доводиться звужувати спочатку знайдені відрізки ізоляції кореня.
З курсу математичного аналізу [3, гл. VII] відомо, що при f '(x)> 0 на [а; b] функція зростає на цьому відрізку; при f '(x) <0 -спадає; при f "(х)> 0 графік функції увігнутий, а при f (х) <0 - опуклий.
Можливі чотири випадки:
1) f '> 0, f "> 0 - функція зростає, графік увігнутий;
2) f '<0, f "<0 - функція убуває, графік опуклий;
3) f '> 0, f "<0 - функція зростає, графік опуклий;
4) f '<0, f "> 0 - функція убуває, графік увігнутий.
Від того, який з випадків має місце, залежить рекурентна формула (в методі хорд) і правило вибору початкового наближення (В обох методах).
Покажемо, що, замінюючи відповідним чином при різних комбінації знаків похідних вихідну функцію f іншими функціями g, можна замість (2.1) розглядати рівняння виду
g(x)=0, (2.1')
для яких має місце тільки один з перерахованих випадків (Наприклад, перший).
Випадок 1. f '(x)> 0 і f"(x)>0 на [а; b]. Можна вважати його основним і саме при таких умовах вирішувати проблему уточнення коренів обома методами. Відповідний графік функції зображений на рис. 2.3.
Випадок 2. f '(x) <0, f " (х)<0 на [а; b]. Візьмемо функцію g: g(х) = - f (x) (рис. 2.5, а). Тоді g '(х) = - f (x)> 0, g "(х) = - f " (x)>0 і приходимо до першого випадку. Зауважимо, що тут рівняння (2.1) і (2.1 ') рівносильні.
Випадок 3. f '(x)> 0 і f "(х) <0 на [а; b]. Нехай g: g(х) = - f (- х) (Рис. 2.5, б). Тоді коренем рівняння (2.1 ') буде - t, а відрізком його ізоляції є [- b; - а]. Для доказу позитивності похідних функції g на [- b; - а] позначимо z = - х. Очевидно, що х є [- b; - а] <=> z є [а; b], тому
Випадок 4. f '(x) <0 і f "(х)> 0 на [а; b]. Покладемо g: g (х) = f (-x) (Рис. 2.5, в). Такими ж міркуваннями, як у випадку 3, показує, що похідні g ' і g " позитивні на [- b; - а].
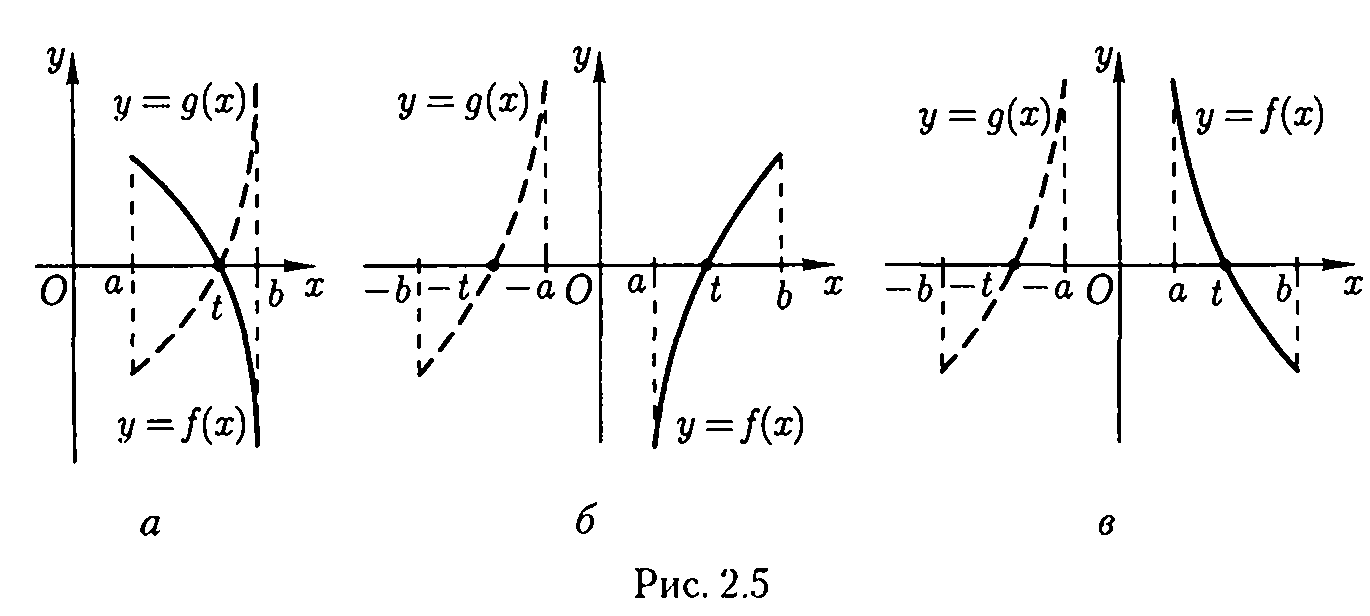
Отже, провівши попереднє дослідження, можна прийти до рівняння виду (2.1) з позитивними похідними f '(x) і f"(x) на відрізках ізоляції кореня. Потім у випадках 3 і 4 замість знайденийного наближення до кореня рівняння (2.1 ') треба взяти це приближення із зворотним знаком.
Приклад 2.4. Корінь рівняння In х =-х відділений на відрізку [0,2; 1].
Тут
f
(х)
=
In
x
+
х.
На
даному
відрізку
f
'(х)
=
+
1>
0,
f
"(x)
=
<0.
Отже,
має
місце
випадок
3
і
вихідне
рівняння можна
замінити
рівнянням
виду
- f (- х) = 0: -(In (-х) - х) = 0 <=> х-In (-х) = 0.
Корінь отриманого рівняння лежить на відрізку [- 1; -0,2]. Неважко перевірити, що похідні g ' і g " функції g: g (х) - х - In (-x) є позитивними на [- 1; -0,2].