
2.2 Відділення коренів
Відділення коренів зазвичай проводиться графічно і (або) аналітично.
Графічний
спосіб відділення коренів рівняння
(2.1) заключає в пошуку таких відрізків
![]() ,
усередині яких знаходиться абсциса
точки перетину графіка функції
,
усередині яких знаходиться абсциса
точки перетину графіка функції ![]() з віссю Ох, тобто
нуль
функції f.
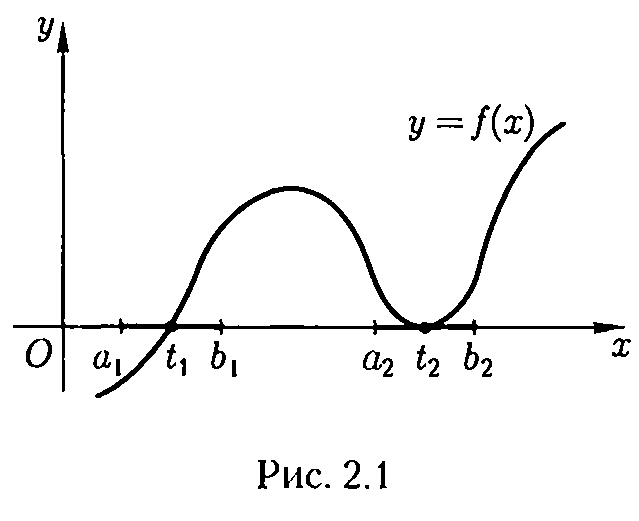
На
рис.
2.1
відзначені два корені з відповідними
їм відрізки.
з віссю Ох, тобто
нуль
функції f.
На
рис.
2.1
відзначені два корені з відповідними
їм відрізки.
У багатьох випадках виявляється зручним замінити рівняння (2.1) рівносильним йому рівнянням
![]()
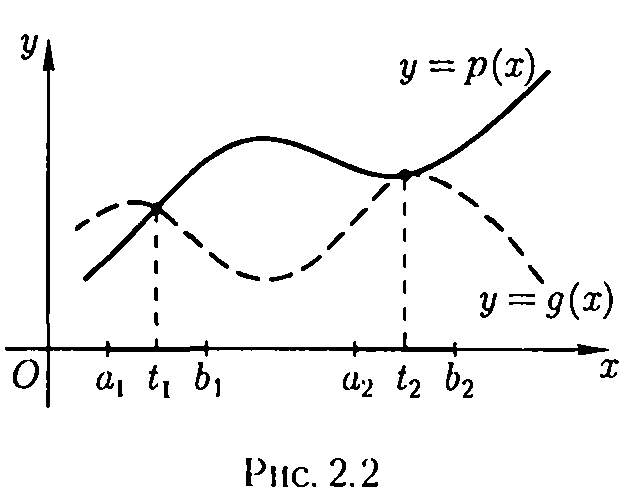
де
р
і
g
-
функції,
графіки
яких будуються
легше,
ніж
графік
функції f.
Коренями
рівняння (2.3) є абсциси точок перетину
ліній ![]() (Рис. 2.2).
(Рис. 2.2).
Графічний спосіб застосоється найбільш часто. Зазвичай з нього і починають відділення коренів, однако він не володіє великою точністю, і тому робити заключні висновки на його основі не завжди вдається.
При схематичному зображення графіків можна помилитися в виборі відрізка ізоляції кореня. Це трапляється, коли необхідний відрізок невеликої довжини або корені розташовані близько. Тут треба врахувати, що наступні методи уточнення вимагають від функцій певних властивостей в околиці кореня. Чим дрібніше відрізок, тим імовірність виконання цих властивостей вище. Буває також, що на деяких дільницях області визначення рівняння графіки функцій розташовуються настільки близько, що встановити факт їх перетину або кількість перетинів важко.
Таким чином, результати графічного методу необхідно провіряти й уточнювати. Робиться це аналітичними методами.
Аналітичний спосіб. Наведені нижче теореми складають основу аналітичного способу відділення коренів.
Т
е о
р е м а 2.1
(перша теорема Больцано-Коші).
Нехай
функція f
визначена і пепреривна
на
відрізку [а; b],
причому на кінцях його приймає
значення різних знаків, тобто
![]() <0.
Тоді
існує
принаймні
одна точка t
є
(а; b),
в якій значення функції дорівнює
нулю [3, гл.
IV,
§ 5].
<0.
Тоді
існує
принаймні
одна точка t
є
(а; b),
в якій значення функції дорівнює
нулю [3, гл.
IV,
§ 5].
Т е о р е м а 2.2. Якщо неперервна на відрізку [а; b] функція f має на (а; b) кінцеву похідну і f '( )> 0 f '( )> 0 для всіх є (а; b), то вона зростає (спадає) на цьому відрізку [3, гл.УП, § 1].
Теорема
2.1
гарантує наявність кореня рівняння
(2.1)
у відрізку
[a;
b],
але не єдиність його.
Як
видно з рис.
2.1,
на
відрізку ![]() виконуються
умови теореми :
f
безперервно,
виконуються
умови теореми :
f
безперервно,
![]() <0, f(
<0, f(![]() >
0, про те там два корня
>
0, про те там два корня
![]()
Зрозуміло,
що корінь, про який йдеться в теоремі
2.1, буде
єдиним,
якщо додатково вимагати від функції
строгу
монотонність на
відрізку (рис. 2.1, відрізок ![]() ).
Для
перевірки
монотонності можна скористатися
теоремою 2.2.
).
Для
перевірки
монотонності можна скористатися
теоремою 2.2.
При чисто аналітичному відділенні коренів рівняння (2.1) корисно обчислити односторонні межі функції f (якщо вони існують) в точках розриву, в кінцях проміжків визначення, а також в ± ∞. Знаки цих меж допоможуть встановити факт перетину графіка функції з віссю Ох (приклад 2.1).
Приклад
2.1.
Рівняння
![]() має
принаймні
один
корінь, тому що функція f:
має
принаймні
один
корінь, тому що функція f:
![]() визначена і
неперервна
на всій дійсній прямій
визначена і
неперервна
на всій дійсній прямій
![]()
Далі береться кілька проміжних точок з області непереривності функції f, підбір яких залежить від її властивостей, і обчислюються значення функції в них. Якщо в двох обраних сусідніх точках з одного і того ж проміжку неперервності функції відбудеться зміна знака, то, згідно теоремі 2.1, між ними є корінь.
Слід
зауважити,
що
теорем
2.1 і
2.2 недостатньо
для
виявлення
та
ізоляції
всіх
коренів
рівняння![]() .
Корінь
може бути всередині [а; b]
і при однакових знаках
.
Корінь
може бути всередині [а; b]
і при однакових знаках ![]()
![]() (рис.
2.1, відрізок
(рис.
2.1, відрізок
![]() Такими
корнями
можуть бути точки максимуму або
мінімума
функції f.
Щоб
їх виявити, не потрібно проводити
повне
дослідження функції на екстремум,
досить знайти підозрілі
на екстремум точки t
і
обчислити в них значення функції.
Якщо
Такими
корнями
можуть бути точки максимуму або
мінімума
функції f.
Щоб
їх виявити, не потрібно проводити
повне
дослідження функції на екстремум,
досить знайти підозрілі
на екстремум точки t
і
обчислити в них значення функції.
Якщо
![]() ,
то t - корінь.
,
то t - корінь.
Корисно знати також теорему Ролля [3, гл. VI, § 1]:
Теорема 2.3. Нехай на [а; b] визначена функція f, причому: 1) f безупинна па [а; b];
2) на (а; b) існує кінцева похідна f ';
3)![]() .
.
Тоді знайдеться точка с є (а; b) така, що f '(с) = 0.
Теорема Ролля допомагає встановлювати, скільки всього різних коренів може бути у рівняння.
Приклад
2.2.
Доведемо,
що рівняння ![]() має
не більше двох коренів.
Тут
має
не більше двох коренів.
Тут
![]() .
Ця
функція визначена і дифференціюєма
на R.
Її
похідна
.
Ця
функція визначена і дифференціюєма
на R.
Її
похідна ![]() дорівнює нулю в одній точці
= 0.
Припустимо,
що рівняння має, наприклад,
три
різних корня
дорівнює нулю в одній точці
= 0.
Припустимо,
що рівняння має, наприклад,
три
різних корня
![]() Тоді
Тоді
![]() тобто
значення функції в трьох точках
рівні.
В
цьому випадку, згідно теоремі
Ролля, між ними знайдуться дві точки,
де похідна перетворюється
в нуль.
А
це суперечить встановленим фактом.
•
тобто
значення функції в трьох точках
рівні.
В
цьому випадку, згідно теоремі
Ролля, між ними знайдуться дві точки,
де похідна перетворюється
в нуль.
А
це суперечить встановленим фактом.
•
Проте
теорема Ролля не стверджує, що корні
є насправді.
Щоб
перевірити їх наявність, треба
скористатися тими методами, що були
наведені
вище.
Наприклад,
для рівняння ![]() ;
має місце ситуація, аналогічна
описаній до прикладу 2.2, однако
це рівняння коренів не має взагалі
(переконайтеся графічно!).
А
от функція f
з цього прикладу змінює знак на
відрізках [-2; -1,5] і [1; 1,5], і тому
рівняння
;
має місце ситуація, аналогічна
описаній до прикладу 2.2, однако
це рівняння коренів не має взагалі
(переконайтеся графічно!).
А
от функція f
з цього прикладу змінює знак на
відрізках [-2; -1,5] і [1; 1,5], і тому
рівняння ![]() = х + 2 має два різних кореня (Але не
більше).
= х + 2 має два різних кореня (Але не
більше).
У наступних параграфах викладаються методи уточнення коренів.
