Модель консервативной системы.

Рассеяние (диссипация) энергии происходит в связи с наличием того или иного вида трения (механическая энергия с течением времени уменьшается за счет преобразования в другие виды энергии, например, в теплоту). В некоторых случаях рассеяние может быть настолько медленным, что им можно пренебречь при исследовании поведения системы для непродолжительного промежутка времени. Системы такого типа называются консервативными.

Механическая энергия консервативной системы (отсутствие рассеяния энергии) сохраняется неизменной в процессе движения системы: имеет место закон сохранения механической энергии - сумма кинетической и потенциальной энергий постоянна в процессе движения системы. Закон справедлив для любой замкнутой системы тел, силы взаимодействия между которыми потенциальны. Если эти силы непотенциальны (например, есть силы трения), то механическая энергия замкнутой системы уменьшается.

Простейший пример консервативной системы: тело совершает горизонтальные движения в вакууме под действием двух пружин.

Е сли х обозначает смещение тела массой m из состояния равновесия, а сила, с которой пружины действуют на тело (восстанавливающая сила), пропорциональна смещению х, то уравнение движения имеет вид md²x/dt² + сx = 0, c > 0.

Восстанавливающая сила является линейной функцией х.

Если тело движется в среде с сопротивлением и сопротивление (демпфирующая сила), действующее на тело, пропорционально скорости движения, то уравнение движения такой неконсервативной системы имеет вид md²x/dt² + c dx/dt + kx = 0.

Здесь демпфирующая сила – линейная функция скорости dx/dt (линейное затухание).

Если f и g являются такими произвольными функциями, что f(0) = 0, g(0) = 0, то более общее уравнение md²x/dt² + g dx/dt + f(x) = 0 является уравнением движения тела массой под действием восстанавливающей и демпфирующей сил.

В общем случае эти силы нелинейны – уравнение рассматривается как основное уравнение нелинейной механики.

Электрическая подсистема.

Электрическая модель является наиболее и универсальной для описания явлений и процессов различной природы.

Типовыми простейшими элементами электрической подсистемы являются резистор с электрическим сопротивлением R, конденсатор без потерь заряда с электрической емкостью C, индуктивная катушка без сопротивления с электрической индуктивностью L.

При описании их функционирования используются переменные: сила тока I, напряжение U. Значение напряжения на элементах совпадает с разностью значений электрического потенциала на концах элементов, напряжение на элементе источника тока равно его ЭДС (электродвижущей силе).

ΔU = IR I  = С dΔU /dt ΔU = L dI /dt.

Резистор является характерным представителем типового элемента, обладающего свойством оказывать сопротивление переносу некоторой физической субстанции (в данном случае электрических зарядов).

Электрический заряд – произведение силы тока I на время протекания тока: q=It, или I= q/t. Для прохождения через такой элемент физического потока необходимо располагать разностью потенциалов на входе в элемент и на выходе из него.

Математическая модель резистора, описывающая протекание через него электрического тока представляет собой алгебраическое уравнение – закон Ома ΔU = IR,

где ΔU – падение электрического напряжения на резисторе (разность электрических потенциалов), I – сила тока.

Электрический конденсатор обладает свойством накапливать электрический заряд пропорционально разности потенциалов ΔU на его обкладках. Энергия электрического поля в конденсаторе равна Е = С (ΔU )²/2.

По физическому смыслу емкости конденсатора С (емкость равна величине заряда, который необходимо помесить на обкладки конденсатора для увеличения разности потенциала между ними на единицу С = q/u) в любой момент времени имеем равенство U_C = q(t)/С.

Для конденсатора с постоянной емкостью С при изменении ΔU в цепи во времени протекает ток силой I. Математическая модель конденсатора представляет собой обыкновенное дифференциальное уравнение 1-го порядка I  = С dΔU /dt.

Индуктивная катушка обладает свойством инерции, проявляющимся в стремлении сохранить поток субстанции неизменным.

При изменении во времени силы тока, протекающего через индуктивную катушку, возникает электродвижущая сила самоиндукции, препятствующая изменению силы тока. Эту ЭДС можно представить как разность потенциалов на концах катушки. Математическая модель индуктивной катушки представляет собой обыкновенное дифференциальное уравнение 1-го порядка

U_L = L dI/dt.

Очевидно, что ток i(t) и напряжение u(t) также являются функциями времени. Производная заряда по времени dq/dt определяет мгновенное значение тока через катушку индуктивности L.

Среди простейших типовых элементов, в которых протекают процессы иной физической природы по сравнению с электрической системой, можно выделить элементы со свойствами, аналогичными свойствам резистора, конденсатора, индуктивной катушки.

Резистор является характерным представителем типового элемента, обладающего свойством оказывать сопротивление переносу некоторой физической субстанции (в данном случае электрических зарядов). Для прохождения через такой элемент физического потока необходимо располагать разностью потенциалов на входе в элемент и на выходе из него.

Конденсатор обладает свойством накапливать эту субстанцию при повышении разности потенциалов. Энергия электрического поля в конденсаторе равна Е = С (ΔU )²/2.

Индуктивная катушка обладает свойством инерции, проявляющимся в стремлении сохранить поток субстанции неизменным.

Элементы электрической схемы объединяются в систему с помощью уравнений равновесия и непрерывности (первый и второй законы Кирхгофа), устанавливающие равенство нулю суммы токов в узлах схемы и суммы напряжений в элементах схемы при их обходе по произвольному контуру:

= 0; = 0,

где n – число ветвей в узлах схемы, к – число элементов в контуре схемы.

Колебательный электрический контур.

При электромагнитных колебаниях периодически колеблются энергии электрического и магнитного полей.

Электромагнитные колебания возникают в колебательном контуре, состоящем из электрического конденсатора емкостью С и индуктивной катушки индуктивностью L (электрическое сопротивление отсутствует).

Если конденсатору сообщить заряд, то разность потенциалов ΔU, существующая на конденсаторе, подается непосредственно на катушку (считаем, что сопротивление отсутствует) – конденсатор будет разряжаться через катушку индуктивности. Ток разрядки создает магнитное поле, которое в свою очередь обеспечит заряд конденсатора, имеющий противоположную полярность. Сила тока и напряжение будут изменяться во времени по периодическому закону. При отсутствии сопротивлений колебания не затухают.

На рисунке приведена аналогия между механическими и электромагнитными колебаниями.

Д ля вывода уравнений электромагнитных колебаний целесообразно рассматривать колебания заряда q, мгновенное значение которого на конденсаторе с емкостью С определяет мгновенное напряжение u_С. Необходимо получить уравнение для изменяющейся со временем величины заряда на обкладках конденсатора q(t).

В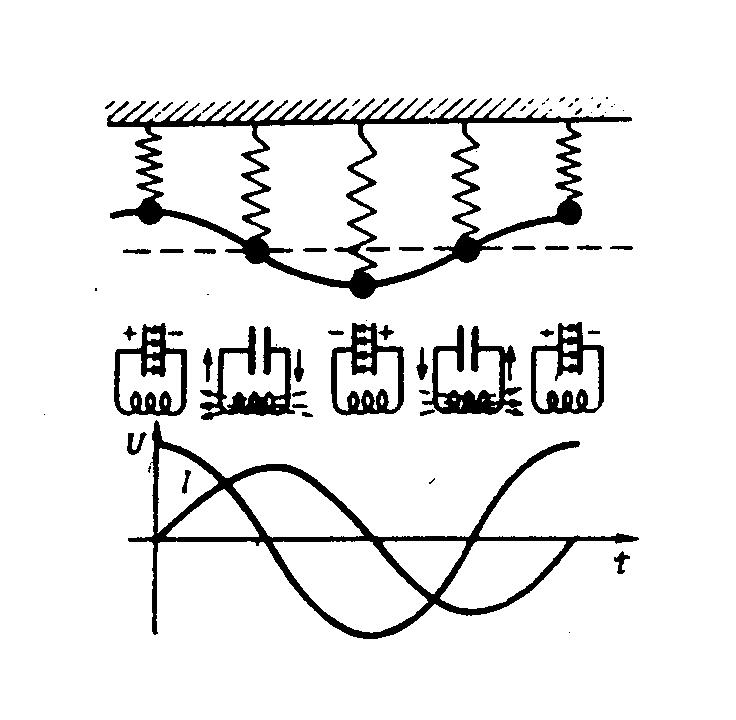 каждый момент времени напряжения на катушке и конденсаторе должны быть равны друг другу:

U_С + U_L = 0, где U_C = q/С, U_L = L di/dt = L d²q/dt².

Отсюда следует L d²q/dt² + q/С = 0,

После деления на L получаем дифференциальное уравнение незатухающих электромагнитных колебаний d²q/dt² + q/(L С) = 0.