§ 3. Повторение измерений
В точности измерения большую роль играет внимание и сосредоточенность экспериментатора, умение выбрать разумный план работы и спокойно, удобно организовать измерение. Нужно правильно расположить оборудование, обеспечить достаточно яркое и равномерное освещение, выбрать удобную позу, периодически делать перерывы в измерениях, своевременно обдумывать предварительные результаты опыта и т.д. Поспешно сделанные измерения обычно никуда не годятся!
Измерение отдельной величины необходимо повторить несколько раз. Такое повторение:
помогает избежать ошибки при снятии показаний приборов и их записи;
дает возможность оценить ошибку измерения.
В вопросе повторения измерения есть одна сторона, которую можно пояснить на одном не столь уж гипотетическом примере. При выполнении задачи к преподавателю обращается студент, который встал перед дилеммой. Он измерил угол призмы при помощи гониометра и получил такие результаты: 56°30' и 60°12'. Точность измерений он оценивает примерно в 5' и, проверив выкладки, приходит к выводу, что один из результатов неверен. (Остановитесь и подумайте, как следовало бы поступить).
Студент спрашивает преподавателя, какой из двух результатов следует считать правильным. Конечно, это смешно. Ведь цель эксперимента – что нибудь найти. Студент же так ничего и не нашел, разве только то, что один из его результатов неверный. (А вполне возможно, что неверны оба). В подобном случае вы обязаны провести дополнительные измерения. Измерения следует повторять до тех пор, пока результаты не приобретут какой-то смысл. А до этого с ними нельзя производить никаких, даже простейших действий. Если следующее измерение дает 56°34', то можно будет подумать, что неверен, вероятно, второй результат. Нужно еще раз измерить угол призмы, и если он окажется равным 56°35', то вы можете быть почти уверены, что оно так и есть. Вы можете даже задуматься над тем, как это вы сумели получить угол, равный 60°12'. Но этого, пожалуй, уже никогда не удастся установить. По-видимому, во время измерений была случайно сдвинута призма, или, что более вероятно, была сбита установка зрительной трубы, или просто неверно произведен отчет. Досадно, когда появляется неверный результат, и вы не можете его объяснить, но так бывает, и если это случается редко, то не следует расстраиваться. Беспокоиться придется в том случае, если:
вы произвольно решите, что угол призмы равен 60°, и поэтому примете второй результат или
решите усреднить первые два результата.
§ 4. Число измерений
Если в задаче исследуется зависимость одной величины от другой, число отдельных точек на различных участках кривой выбирается с таким расчетом, чтобы подробно исследовать места изгибов, максимумов, крутых скачков. В тех участках, где кривая идет плавно, ставить особенно много точек не имеет большого смысла.
Область изменения переменных следует брать как можно шире, т.к. на границах широкого интервала часто нагляднее обнаруживаются недостатки аппаратуры и новые явления, влияние которых начинает обычно сказываться существенно раньше, но не может быть там с достоверностью обнаружено. Перед началом работы полезно произвести несколько предварительных измерений по всему диапазону изменения переменных, чтобы сразу познакомиться с основными чертами явления и правильно спланировать ход эксперимента.
В конце работы обязательно надо возвращаться к началу кривой и повторить первые измерения. Это позволит проверить стабильность установки. Еще лучше проделать все измерения в обратном порядке. При этом могут быть обнаружены и новые интересные подробности в самом явлении (гистерезис).
ЗАПИСЬ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА § 1. Таблицы Старайтесь всегда записывать результаты измерений в виде таблиц. Такая запись компактнее и проще для чтения. Значения одной и той же величины лучше всего записывать в вертикальный столбик, ибо глазу легче сопоставлять цифры, расположенные столбиком. В начале каждого столбца напишите название или символ соответствующей величины и укажите единицу измерения. Для удобства следует придать единице измерения такой десятичный множитель, чтобы записываемые значения были заключены в интервале примерно от 0.1 до 1000. Рассмотрим таблицу, которая представляет собой лишь начало большой таблицы значений модуля Юнга для разных материалов.
Модуль Юнга для железа равен 2.11·1011 H·м-2 . Рекомендуем вам пользоваться записью, при которой после физической величины просто ставят запятую и указывают единицу измерения – в данном случае 1011 H·м-2. Такая запись понятна и вряд ли может вызвать недоумение. Коль скоро единица измерения указана в начале столбца, нет необходимости повторять ее при каждом значении. Вообще следует избегать ненужных повторений. Это потеря времени, энергии и загромождение записи. Чем меньше второстепенного, тем легче увидеть главное. § 2. Запись измерений Все результаты измерений следует записывать немедленно и без какой либо обработки. Из этого правила нет исключений. Не производите никаких – даже самых простых –арифметических расчетов в уме, прежде чем записать результат измерения. Допустим, например, что для получения тока в амперах показания амперметра следует делить на 2. Прежде всего, запишите показания прибора в делениях шкалы и не делите предварительно пополам. Почему следует так поступать, ясно: если при делении в уме вы допустите ошибку, то позже исправить ее уже не сможете. При проведении и записи измерений хорошо проверить то, что вы записали, взглянув еще раз на прибор. Итак: посмотрите, запишите, проверьте. Об обработке результатов будет подробно рассказано в последующих разделах, а здесь мы сделаем лишь общее замечание. Очень плохо, когда проводят все новые и новые измерения, а их результаты обрабатывают лишь в конце эксперимента. При обработке части результатов нередко обнаруживается какое-либо расхождение, которое приводит к необходимости внести те или иные изменения в аппаратуру. Кроме того, сама работа часто ведется так, что одной серией результатов может определиться дальнейшее направление эксперимента. И уж самое глупое, что можно сделать, – это разобрать сложную установку до того, как обработать результаты (так тоже случается). § 3. Избегайте переписывания У многих студентов очень плохая привычка записывать результаты наблюдений сначала на клочке бумаги или в «черновой» тетради, затем переписывать их в «чистовую» тетрадь, а оригинал уничтожать. Против этого можно выдвинуть три возражения:
Последнее обстоятельство особенно важно, и его следует разобрать подробнее. В большинстве экспериментов используются не все данные измерения. Часто мы приходим к заключению, что некоторые из них либо не очень показательны, либо получены в неподходящих условиях, либо просто не имеют отношения к делу. Иными словами, мы отбираем. Все это совершенно правильно, если при отборе мы руководствуемся объективными критериями. Но все первичные данные измерений надо обязательно сохранять. В дальнейшем может понадобиться и другой отбор. Во всяком случае, все экспериментальные данные должны быть налицо, чтобы и другие могли судить по ним о правильности произведенного отбора и о характере самих измерений. Важная задача практического курса физики состоит в том, чтобы научить четкой и эффективной записи, и, прежде всего, нужно научиться записывать непосредственно измеряемые величины. На первом этапе в этом вам помогут готовые формы таблиц, приводимые в описаниях работ, затем такие таблицы вы должны будете составлять самостоятельно. Постепенно вы накопите опыт, и дело пойдет на лад. И если ваша запись не будет выглядеть так красиво, как бы она выглядела после переписывания, не это важно. В записи красота, конечно, важна, но еще важнее ясность. § 4. Схемы Есть древняя китайская пословица: «Один рисунок лучше тысячи слов». Важное значение схем в записях эксперимента и в отчетах об эксперименте вряд ли можно переоценить. Дополненная несколькими словами схема часто оказывается самым простым и самым хорошим способом объяснения идеи эксперимента, описания установки и введения обозначений. Для примера приведем два разных описания одного и того же элемента установки для исследования колебаний пары связанных маятников.
О
Рис.
1 Описание 2. Схема установки представлена на рис.1. AP1P2B – цельный отрезок нити, P1 и P2– скользящие узлы. Связь изменяем, изменяя х за счет перемещения узлов, причем y1 = y2. Комментарии к этим описаниям излишни. Схема не должна быть художественным или фотографически точным изображением установки. Она должна быть как можно проще, и на ней должно быть указано только то, что имеет отношение к эксперименту. Далее, хотя часто бывает полезно вычертить полную схему установки с приблизительным соблюдением масштаба, на других схемах без всяких колебаний следует сильно искажать масштаб, если это позволяет четче выявить ту или иную особенность.
§ 5. Что еще способствует ясности
Схемы и таблицы – это две формы записи, которые позволяют добиться большой ясности. Но следует приветствовать и все иное, что направлено к той же цели. Группы данных измерения разных величин необходимо разделять достаточно большими пробелами и каждой из них давать заголовок. Если серию измерений вы сводите к одному значению, скажем к среднему, то полезно его не только соответственно обозначить, но и подчеркнуть, или как-то иначе выделить. Вообще говоря, при ведении записи не нужно слишком экономить бумагу. Привычка к исправлению цифр – враг ясности. Не заставляйте всякого, читающего ваши записи, да и себя тоже, по истечении некоторого времени ломать голову над исправленными цифрами. Лучше зачеркнуть неверные цифры и написать рядом правильно. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ГРАФИКИ § 1. Для чего нужны графики?
В экспериментальной физике графиками пользуются для разных целей. Во-первых, графики строят, чтобы определить некоторые величины, – обычно наклон или отрезок, отсекаемый на оси координат, прямой, изображающей зависимость между двумя переменными. Хотя в элементарных курсах физики упор часто делается именно на это, на самом деле роль графика здесь сравнительно невелика. Ведь при методе наименьших квадратов наклон прямой определяют, конечно, не по графикам, как таковым, а по исходным числовым данным. Непосредственно же по графику определить наклон можно только в том случае, если провести через точки на глаз наилучшую прямую. Это довольно грубый метод. Его не следует сбрасывать со счета, но он пригоден лишь тогда, когда мы оценивает результат, полученный наиболее точным методом или когда наклон кривой не очень важен для окончательного результата. Во-вторых, и это, пожалуй, самое главное, – графиками пользуются для наглядности. Допустим, например, что мы измеряем скорость течения воды по трубке как функцию перепада давления с целью определить, когда поток перестает быть ламинарным и становится турбулентным. Полученные данные приведены в таблице 1. Таблица 1.
Пока поток остается ламинарным, скорость его пропорциональна перепаду давления. Глядя на цифры, приведенные в таблице, трудно сказать, где пропорциональность начинает нарушаться. Другое дело, когда те же данные, представлены графиком (рис.2). В этом случае сразу видна точка, в которой нарушается пропорциональность. Графики позволяют также более наглядно проводить сравнение экспериментальных данных с теоретической кривой. Нанося результаты измерений на график, очень удобно следить за тем, как идет эксперимент. В
§ 2. Масштаб
В физике на графиках принято по горизонтальной оси откладывать независимую переменную, т.е. величину, значение которой задает сам экспериментатор, а по вертикальной оси – ту величину, которую он при этом определяет. Короче говоря, по горизонтали откладывается «причина», а по вертикали – «следствие». Существуют различные виды бумаги для графиков, но из них в физике наиболее употребительны два: с обычным линейным масштабом (миллиметровая) и логарифмическая. Последняя бывает двух видов: полулогарифмическая, когда логарифмический масштаб взят только на одной оси координат, и двойная логарифмическая, когда такой масштаб удобно использовать для изображения изучаемой величины, изменяющейся на несколько порядков в пределах измерений. Полулогарифмическая бумага удобна в том случае, когда связь между переменными логарифмическая или экспоненциальная (y = Bo + B1ekx). Если же эта связь имеет вид y ~ xk , где k – неизвестная величина, то лучше взять двойную логарифмическую бумагу.
Допустим, что мы взяли миллиметровую бумагу. При выборе масштаба нужно исходить из следующих соображений:
§ 3. Единицы измерения
Как и в случае с таблицами, десятичный множитель удобнее отнести к единице измерения. Тогда деления на графике можно помечать цифрами 1, 2, 3 ... или 10, 20, 30 ..., а не 10000, 20000 и т.д., или 0.0001, 0.0002 и т.д. На осях координат следует указать название или символ (или то и другое). Единицы измерений нужно указывать тем же способом, что и в таблицах, а именно десятичный множитель относить к единице измерения. См. на рис.7 пример, показывающий, как делать надписи вдоль осей графика и как указывать единицы измерения.
§ 4. Как строить графики
Графики делают в основном для того, чтобы наглядно представить результаты эксперимента, и потому они должны быть предельно ясными. Ниже мы дадим ряд общих советов по вычерчиванию графиков. Пользоваться ими нужно с учетом особенностей каждого конкретного случая.
Рис.8 – пример неудачного графика, на котором экспериментальные точки очень мелкие и не отличаются от расчетных точек, по которым проведена теоретическая кривая. Рис.9 – расчетные точки не видны, а экспериментальные точки четко выделяются.
а отклонения точек вызваны«шумом» эксперимента, случайными ошибками при измерениях. При проведении кривой следует руководствоваться правилами:
Если на графике имеется теоретическая кривая, то «плавную» кривую через экспериментальные точки лучше не проводить. Такая кривая, может быть, не совсем соответствует фактическим данным, и тогда она будет мешать прямому сравнению эксперимента с теорией.
§ 5. Как указывать ошибки
Ошибку в экспериментальном значении
можно указать следующим образом:
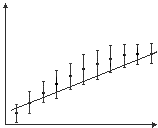
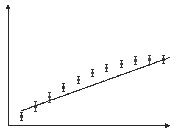
Экспериментальная точка находится в середине отрезка, изображающего величину ошибки. Поскольку нанесение таких значков – дополнительный труд и приводит к усложнению графика, это следует делать лишь в том случае, когда без такой информации обойтись нельзя, т.е. когда от ошибок может зависеть значимость отклонения экспериментальных данных от теоретической кривой (см. рис.12 и 13). Отклонения экспериментальных точек от прямой линии на обоих графиках одинаковы, но на рис.12 отклонения вряд ли значимы, а на рис.13, по-видимому, значимы. Ошибки обычно указывают и еще в одном случае, – когда они неодинаковы для разных экспериментальных точек. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ § 1. Виды измерений
Измерением какой-либо величины называется операция, в результате которой мы узнаем, во сколько раз измеряемая величина больше (или меньше) соответствующей величины, принятой за эталон (единицу измерения). Все измерения можно разбить на два типа: прямые и косвенные. ПРЯМЫЕ – это такие измерения, при которых измеряется непосредственно интересующая нас физическая величина (масса, длина, интервалы времени, изменение температуры и т.д.). КОСВЕННЫЕ – это такие измерения, при которых интересующая нас величина определяется (вычисляется) из результатов прямых измерений других величин, связанных с ней определенной функциональной зависимостью. Например, определение скорости равномерного движения по измерениям пройденного пути промежутка времени, измерение плотности тела по измерениям массы и объема тела и т.д. Общая черта измерений – невозможность получения истинного значения измеряемой величины, результат измерения всегда содержит какую-то ошибку (погрешность). Объясняется это как принципиально ограниченной точностью измерения, так и природой самих измеряемых объектов. Поэтому, чтобы указать, насколько полученный результат близок к истинному значению, вместе с полученным результатом указывают ошибку измерения. Например, мы измерили фокусное расстояние линзы f и написали, что f = (256 ± 2) мм (1) Это означает, что фокусное расстояние лежит в пределах от 254 до 258 мм. Но на самом деле это равенство (1) имеет вероятностный смысл. Мы не можем с полной уверенностью сказать, что величина лежит в указанных пределах, имеется лишь некоторая вероятность этого, поэтому равенство (1) нужно дополнить еще указанием вероятности, с которой это соотношение имеет смысл (ниже мы сформулируем это утверждение точнее). Оценка ошибок необходима, т.к., не зная, каковы они, нельзя сделать определенных выводов из эксперимента. Обычно рассчитывают абсолютную и относительную ошибку. Абсолютной ошибкой Δx называется разность между истинным значением измеряемой величины μ и результатом измерения x, т.е. Δx = μ – x. Отношение абсолютной ошибки к истинному значению измеряемой величины ε = (μ - x)/μ и называется относительной ошибкой. Абсолютная ошибка характеризует погрешность метода, который был выбран для измерения. Относительная ошибка характеризует качество измерений. Точностью измерения называют величину, обратную относительной ошибке, т.е. 1/ε.
§ 2. Классификация ошибок
Все ошибки измерения делятся на три класса: промахи (грубые ошибки), систематические и случайные ошибки. ПРОМАХ вызван резким нарушением условий измерения при отдельных наблюдениях. Это ошибка, связанная с толчком или поломкой прибора, грубым просчетом экспериментатора, непредвиденным вмешательством и т.д. грубая ошибка появляется обычно не более чем в одном–двух измерениях и резко отличается по величине от прочих ошибок. Наличие промаха может сильно исказить результат, содержащий промах. Проще всего, установив причину промаха, устранить его в процессе измерения. Если в процессе измерения промах не был исключен, то это следует сделать при обработке результатов измерений, использовав специальные критерии, позволяющие объективно выделить в каждой серии наблюдений грубую ошибку, если она имеется. СИСТЕМАТИЧЕСКОЙ ОШИБКОЙ называют составляющую погрешности измерений, остающуюся постоянной и закономерно изменяющуюся при повторных измерениях одной и той же величины. Систематические ошибки возникают, если не учитывать, например, теплового расширения при измерениях объема жидкости или газа, производимых при медленно меняющейся температуре; если при измерении массы не принять во внимание действие выталкивающей силы воздуха на взвешиваемое тело и на разновесы и т.д. Систематические ошибки наблюдаются, если шкала линейки нанесена неточно (неравномерно); капилляр термометра в разных участках имеет разное сечение; при отсутствии электрического тока через амперметр стрелка прибора стоит не на нуле и т.д. Как видно из примеров, систематическая ошибка вызывается определенными причинами, величина ее остается постоянной (смещение нуля шкалы прибора, неравноплечность весов), либо изменяется по определенному (иногда довольно сложному) закону (неравномерность шкалы, неравномерность сечения капилляра термометра и т.д.). Можно сказать, что систематическая ошибка – это смягченное выражение, заменяющее слова «ошибка экспериментатора». Такие ошибки возникают из-за того, что:
Как поступать в первом случае, мы знаем, – нужна калибровка или градуировка. В двух других случаях готового рецепта не существует. Чем лучше вы знаете физику, чем больше у вас опыта, тем больше вероятность, что вы обнаружите подобные эффекты, а значит, и устраните их. Общих правил, рецептов для выявления и устранения систематических ошибок нет, но некоторую классификацию можно провести. Выделим четыре типа систематических ошибок.
Пример. Взвешивание на неравноплечных весах. Пусть разность длин плеч – 0.001 мм. При длине коромысла 70 мм и массе взвешиваемого тела 200 г систематическая ошибка составит 2.86 мг. Систематическую ошибку этого измерения можно устранить, применяя специальные методы взвешивания (метод Гаусса, метод Менделеева и т.д.).
Пример. В паспорте, прилагаемом к микрометру, написано: «допустимая погрешность составляет ±0.004 мм. Температура +20 ± 4° C. Это означает, что, измеряя данным микрометром размеры какого-нибудь тела при указанных в паспорте температурах, мы будем иметь абсолютную погрешность, не превышающую ± 0.004 мм при любых результатах измерений. Часто максимальная абсолютная ошибка, даваемая данным прибором, указывается с помощью класса точности прибора, который изображается на шкале прибора соответствующим числом, чаще всего взятым в кружок. Число, обозначающее класс точности, показывает максимальную абсолютную ошибку прибора, выраженную в процентах от наибольшего значения измеряемой величины на верхнем пределе шкалы. Пусть в измерениях использован вольтметр, имеющий шкалу от 0 до 250 В, класс точности его – 1. Это значит, что максимальная абсолютная ошибка, которая может быть допущена при измерении этим вольтметром, будет не больше 1% от наибольшего значения напряжения, которое можно измерить на этой шкале прибора, иначе говоря: δ = ±0.01·250В = ±2.5В. Класс точности электроизмерительных приборов определяет максимальную погрешность, величина которой не меняется при переходе от начала к концу шкалы. Относительная ошибка при этом резко меняется, потому приборы обеспечивают хорошую точность при отклонении стрелки почти на всю шкалу и не дают ее при измерениях в начале шкалы. Отсюда следует рекомендация: выбрать прибор (или шкалу многопредельного прибора) так, чтобы стрелка прибора при измерениях заходила за середину шкалы. Если класс точности прибора не указан и нет паспортных данных, то в качестве максимальной ошибки прибора берется половина цены наименьшего деления шкалы прибора. Несколько слов о точности линеек. Металлические линейки очень точны: миллиметровые деления наносятся с погрешностью не более ±0.05 мм, а сантиметровые не хуже, чем с точностью 0.1 мм. Погрешность измерений, производимых с точностью таких линеек, практически равна погрешности отсчета на глаз (≤0.5 мм). Деревянными и пластиковыми линейками лучше не пользоваться, их погрешности могут оказаться неожиданно большими. Исправный микрометр обеспечивает точность 0.01 мм, а погрешность измерений штангенциркулем определяется точностью, с которой может быть сделан отсчет, т.е. точностью нониуса (обычно 0.1 мм или 0.05 мм).
Пример. Определяется электропроводность некоторого материала. Если для такого измерения взят отрезок проволоки, имеющей какой-то дефект (утолщение, трещину, неоднородность), то в определении электропроводности будет допущена ошибка. Повторение измерений дает такое же значение, т.е. допущена некоторая систематическая ошибка. Измерим сопротивление нескольких отрезков такой проволоки и найдем среднее значение электропроводности данного материала, которая может быть больше или меньше электропроводности отдельных измерений, следовательно, ошибки, допущенные в этих измерениях, можно отнести к так называемым случайным ошибкам.
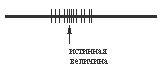
Пример. Определяем плотность какого-либо металла. Вначале находим объем и массу образца. Внутри образца содержится пустота, о которой мы ничего не знаем. В определении плотности будет допущена ошибка, которая повторится при любом числе измерений. Приведенный пример прост, источник погрешности и ее величину можно определить без больших затруднений. Ошибки, такого типа можно выявить с помощью дополнительных исследований, путем проведения измерений совсем другим методом и в других условиях. СЛУЧАЙНОЙ называют составляющую погрешности измерений, изменяющуюся случайным образом при повторных измерениях одной и той же величины. При проведении с одинаковой тщательностью и в одинаковых условиях повторных измерений одной и той же постоянной неизменяющейся величины мы получаем результаты измерений – некоторые из них отличаются друг от друга, а некоторые совпадают. Такие расхождения в результатах измерений говорят о наличии в них случайных составляющих погрешности. Случайная погрешность возникает при одновременном воздействии многих источников, каждый из которых сам по себе оказывает незаметное влияние на результат измерения, но суммарное воздействие всех источников может оказаться достаточно сильным. Случайная ошибка может принимать различные по абсолютной величине значения, предсказать которые для данного акта измерения невозможно. Эта ошибка в равной степени может быть как положительной, так и отрицательной. Случайные ошибки всегда присутствуют в эксперименте. При отсутствии систематических ошибок они служат причиной разброса повторных измерений относительно истинного значения (рис.14). Если, кроме того, имеется и систематическая ошибка, то результаты измерений будут разбросаны относительно не истинного, а смещенного значения (рис.15).
Рис. 14
Допустим, что при помощи секундомера измеряют период колебаний маятника, причем измерение многократно повторяют. Погрешности пуска и остановки секундомера, ошибка в величине отсчета, небольшая неравномерность движения маятника – все это вызывает разброс результатов повторных измерений и поэтому может быть отнесено к категории случайных ошибок. Если других ошибок нет, то одни результаты окажутся несколько завышенными, а другие несколько заниженными. Но если, помимо этого, часы еще и отстают, то все результаты будут занижены. Это уже систематическая ошибка. Некоторые факторы могут вызвать одновременно и систематические и случайные ошибки. Так, включая и выключая секундомер, мы можем создать небольшой нерегулярный разброс моментов пуска и остановки часов относительно движения маятника и внести тем самым случайную ошибку. Но если к тому же мы каждый раз торопимся включить секундомер и несколько запаздываем выключить его, то это приведет к систематической ошибке. Случайные погрешности вызываются ошибкой параллакса при отсчете делений шкалы прибора, сотрясении фундамента здания, влиянием незначительного движения воздуха и т.п. Хотя исключить случайные погрешности отдельных измерений невозможно, математическая теория случайных явлений позволяем уменьшить влияние этих погрешностей на окончательный результат измерений. Ниже будет показано, что для этого необходимо произвести не одно, а несколько измерений, причем, чем меньшее значение погрешности мы хотим получить, тем больше измерений нужно провести. Следует иметь в виду, что если случайная погрешность, полученная из данных измерений, окажется значительно меньше погрешности, определяемой точностью прибора, то, очевидно, что нет смысла пытаться еще уменьшить величину случайной погрешности – все равно результаты измерений не станут от этого точнее. Наоборот, если случайная погрешность больше приборной (систематической), то измерение следует провести несколько раз, чтобы уменьшить значение погрешности для данной серии измерений и сделать эту погрешность меньше или одного порядка с погрешностью прибора.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 3. Обработка результатов прямого измерения Для уменьшения влияния случайных ошибок необходимо произвести измерение данной величины несколько раз. Предположим, что мы измеряем некоторую величину x. В результате проведенных измерений мы получили значений величины : x1, x2, x3, ... xn. (2)
Этот ряд значений величины x получил
название выборки. Имея такую выборку,
мы можем дать оценку результата
измерений. Величину, которая будет
являться такой оценкой, мы обозначим
µ = ± Δx (3) Так как оценочные значения результата измерений и ошибки Δx не являются точными, запись (3) результата измерений должна сопровождаться указанием его надежности P. Под надежностью или доверительной вероятностью понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью (3). Сам этот интервал называется доверительным интервалом. Например, измеряя длину некоторого отрезка, окончательный результат мы записали в виде l = (8.34 ± 0.02) мм, (P = 0.95) Это означает, что из 100 шансов – 95 за то, что истинное значение длины отрезка заключается в интервале от 8.32 до 8.36 мм . Таким образом, задача заключается в том, чтобы, имея выборку (2), найти оценку результата измерений , его ошибку Δx и надежность P. Эта задача может быть решена с помощью теории вероятностей и математической статистики. В большинстве случаев случайные ошибки подчиняются нормальному закону распределения, установленного Гауссом. Нормальный закон распределения ошибок выражается формулой
где Δx – отклонение от величины истинного значения; σ – истинная среднеквадратичная ошибка; σ 2– дисперсия, величина которой характеризует разброс случайных величин. Как видно из (4) функция имеет максимальное значение при x = 0 , кроме того, она является четной. На рис.16 показан график этой функции. Смысл функции (4) заключается в том, что площадь фигуры, заключенной между кривой, осью Δx и двумя ординатами из точек Δx1 и Δx2 (заштрихованная площадь на рис.16) численно равна вероятности, с которой любой отсчет попадет в интервал (Δx1,Δx2). П
где – n число измерений. Итак, если в одних и тех же условиях проделано n измерений, то наиболее вероятным значением измеряемой величины будет ее среднее значение (арифметическое). Величина стремится к истинному значению μ измеряемой величины при n → ∞. Средней квадратичной ошибкой отдельного результата измерения называется величина
Она характеризует ошибку каждого отдельного измерения. При n → ∞ S стремится к постоянному пределу σ σ = lim S. (7) n → ∞ С увеличением σ увеличивается разброс отсчетов, т.е. становится ниже точность измерений. Среднеквадратичной ошибкой среднего арифметического называется величина
Это фундаментальный закон
возрастания точности при росте числа
измерений. Ошибка
Эта методика расчета ошибок дает хорошие результаты (с надежностью 0.68) только в том случае, когда одна и та же величина измерялась не менее 30 – 50 раз. В 1908 году Стьюдент показал, что статистических подход справедлив и при малом числе измерений. Распределение Стьюдента при числе измерений n → ∞ переходит в распределение Гаусса, а при малом числе отличается от него. Для расчета абсолютной ошибки при малом количестве измерений вводится специальный коэффициент, зависящий от надежности P и числа измерений n, называемый коэффициентом Стьюдента t. Опуская теоретические обоснования его введения, заметим, что Δx = · t. (10) где Δx – абсолютная ошибка для данной доверительной вероятности; – среднеквадратичная ошибка среднего арифметического. Коэффициенты Стьюдента приведены в таблице 2. Из сказанного следует:
Таблица 2
Таблица 3
При обработке результатов прямых измерений предлагается следующий порядок операций:
= Σ x i / n.
(Δx 1)2, (Δx 2)2, ... , (Δx n)2.
Δx = · t.
Если одна из ошибок меньше другой в три или более раз, то меньшую отбросьте.
.
Рассмотрим на числовом примере применение приведенных выше формул.
Пример. Измерялся микрометром
диаметр d стержня (систематическая
ошибка измерения равна 0.005 мм ).
Результаты измерений заносим во
вторую графу таблицы, находим
и
в третью графу этой таблицы записываем
разности
Таблица 4
Задавшись надежностью P = 0.95, по таблице коэффициентов Стьюдента для шести измерений найдем t = 2.57. Абсолютная ошибка найдется по формуле (10). Δd = 0.01238 · 2.57 = 0.04 мм. Сравним случайную и систематическую ошибки:
следовательно, δ = 0.005 мм можно отбросить. Окончательный результат запишем в виде d = (4.01 ± 0.04) мм при Р = 0.95.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 4. Округление результатов
Обработка результатов измерений в лабораториях проводятся на калькуляторах и ПК, и просто удивительно, как магически действует на многих студентов длинных ряд цифр после запятой. «Так точнее» – считают они. Однако легко видеть, например, что запись a = 2.8674523 ± 0.076 бессмысленна. При ошибке 0.076 последние пять цифр числа не означает ровно ничего. Если мы допускаем ошибку в сотых долях, то тысячным, тем более десятитысячным долям веры нет. Грамотная запись результата была бы 2.87 ± 0.08. Всегда нужно производить необходимые округления, чтобы не было ложного впечатления о большей, чем это есть на самом деле, точности результатов. Правила округления
243.871±0.026≈243.87±0.03; 243.871±2.6≈244±3; 1053 ± 47 ≈ 1050 ± 50.
Примеры: 8.337 (округлить до десятых) ≈ 8.3; 833.438 (округлить до целых) ≈ 833; 0.27375 (округлить до сотых) ≈ 0.27.
8.3351 (округлить дл сотых) ≈ 8.34; 0.2510 (округлитьь до десятых) ≈ 0.3; 271.515 (округлить до целых) ≈ 272.
Примеры: 0.875 (округлить до сотых) ≈ 0.88; 0.5450 (округлить до сотых) ≈ 0.54; 275.500 (округлить до целых) ≈ 276; 276.500 (округлить до целых) ≈ 276. Примечание.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 5. Обработка косвенных измерений
В лабораторной практике большинство измерений – косвенные и интересующая нас величина является функцией одной или нескольких непосредственно измеряемых величин: N = ƒ (x, y, z, ...) (13) Как следует из теории вероятностей, среднее значение величины определяется подстановкой в формулу (13) средних значений непосредственно измеряемых величин, т.е. ¯N = ƒ (¯x, ¯y, ¯z, ...) (14) Требуется найти абсолютную и относительную ошибки этой функции, если известны ошибки независимых переменных. Рассмотрим два крайних случая, когда ошибки являются либо систематическими, либо случайными. Единого мнения относительно вычисления систематической ошибки косвенных измерений нет. Однако, если исходить из определения систематической ошибки как максимально возможной ошибки, то целесообразно находить систематическую ошибку по формулам
где Для нахождения случайной ошибки косвенных измерений следует пользоваться формулами:
где Δx, Δy, Δz, ... – доверительные интервалы при заданных доверительных вероятностях (надежностях) для аргументов x, y, z, ... . Следует иметь в виду, что доверительные интервалы Δx, Δy, Δz, ... должны быть взяты при одинаковой доверительной вероятности P1 = P2 = ... = Pn = P. В этом случае надежность для доверительного интервала ΔN будет тоже P. Формулой (17) удобно пользоваться в случае, если функция N = ƒ(x, y, z, ...) имеет вид суммы или разности аргументов. Формулой (18) удобно пользоваться в случае, если функция N = ƒ(x, y, z, ...) имеет вид произведения или частного аргументов. Часто наблюдается случай, когда систематическая ошибка и случайная ошибка близки друг к другу, и они обе в одинаковой степени определяют точность результата. В этом случае общая ошибка ∑ находится как квадратичная сумма случайной Δ и систематической δ ошибок с вероятностью не менее чем P, где P – доверительная вероятность случайной ошибки:
При проведении косвенных измерений в невоспроизводимых условиях функцию находят для каждого отдельного измерения, а доверительный интервал вычисляют для получения значений искомой величины по тому же методу, что и для прямых измерений. Следует отметить, что в случае функциональной зависимости, выраженной формулой, удобной для логарифмирования, проще сначала определить относительную погрешность, а затем из выражения ΔN = ε ¯N найти абсолютную погрешность. Прежде чем приступать к измерениям, всегда нужно подумать о последующих расчетах и выписать формулы, по которым будут рассчитываться погрешности. Эти формулы позволят понять, какие измерения следует производить особенно тщательно, а на какие не нужно тратить больших усилий. При обработке результатов косвенных измерений предлагается следующий порядок операций:
N = ƒ (¯x, ¯y, ¯z, ...) ± Δƒ.
ε = Δƒ · 100%. ¯ƒ¯ Приведем примеры расчета ошибки косвенного измерения. Пример 1. Находится объем цилиндра по формуле V = π d2 h , ¯¯¯4¯¯ где d – диаметр цилиндра, h – высота цилиндра. Обе эти величины определяются непосредственно. Пусть измерение этих величин дало следующие результаты: d = (4.01 ± 0.03) мм , h = (8.65 ± 0.02) мм, при одинаковой надежности Р = 0.95. Среднее значение объема, согласно (14) равно V = 3.14 · (4.01)2 · 8.65 = 109.19 мм3 ¯¯¯¯¯¯¯¯¯4¯¯¯¯¯¯¯¯ Воспользовавшись выражением (18) имеем: ln V = ln π + 2 lnd + lnh - ln4;
Так как измерения производились микрометром, цена деления которого 0.01 мм, систематические ошибки δd = δh = 0.01 мм. На основании (16) систематическая ошибка δV будет
Систематическая ошибка оказывается сравнимой со случайной, следовательно
Таким образом, результат измерения оказывается V = (109 ± 2) мм3 при P = 0.95
Пример 2. Найти абсолютную и относительную погрешности для следующей функциональной зависимости:
В этом случае удобнее сначала искать относительную погрешность. Тогда
= d[ln(m1 + m2 - m3)] - d(ln2) - d(ln m1) - d(ln m2) =
До сих пор подразумевается математический смысл дифференциала, и знаки слагаемых учитываются. Раскроем теперь выражение d(m1 + m2 - m3) = dm1 + dm2 - dm3 и разделим почленно на знаменатель. Затем объединим все члены, содержащие дифференциалы одной и той же переменной:
Используя формулу (18), получим
Абсолютную случайную погрешность найдем из выражения Δτ = ε ·¯¯τ Используя формулу (16) получаем
Абсолютную систематическую ошибку найдем из выражения δτ = ε ·¯¯τ Приведем таблицы 5 и 6
Таблица 5 расчета систематических погрешностей для простейших функций. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Таблица 6 расчета случайных погрешностей для простейших функций.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 6. Метод наименьших квадратов
Если некоторая физическая величина зависит от другой величины, то эту зависимость можно исследовать, измеряя y при различных значениях x . В результате измерений получается ряд значений: x1, x2, ..., xi, , ... , xn; y1, y2, ..., yi, , ... , yn. По данным такого эксперимента можно построить график зависимости y = ƒ(x). Полученная кривая дает возможность судить о виде функции ƒ(x). Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Определить их позволяет метод наименьших квадратов. Экспериментальные точки, как правило, не ложатся точно на кривую. Метод наименьших квадратов требует, чтобы сумма квадратов отклонений экспериментальных точек от кривой, т.е. [yi – ƒ(xi)]2 была наименьшей. На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости, т.е. когда y = kx или y = a + bx. Линейная зависимость очень широко распространена в физике. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию. Например, если предполагают, что показатель преломления стекла n связан с длиной λ световой волны соотношением n = a + b/λ2, то на графике строят зависимость n от λ-2. Рассмотрим зависимость y = kx (прямая, проходящая через начало координат). Составим величину φ – сумму квадратов отклонений наших точек от прямой
Величина φ всегда положительна и оказывается тем меньше, чем ближе к прямой лежат наши точки. Метод наименьших квадратов утверждает, что для k следует выбирать такое значение, при котором φ имеет минимум
Вычисление показывает, что среднеквадратичная ошибка определения величины k равна при этом
где – n число измерений. Рассмотрим теперь несколько более трудный случай, когда точки должны удовлетворить формуле y = a + bx (прямая, не проходящая через начало координат). Задача состоит в том, чтобы по имеющемуся набору значений xi, yi найти наилучшие значения a и b. Снова составим квадратичную форму φ , равную сумме квадратов отклонений точек xi, yi от прямой
и найдем значения a и b , при которых φ имеет минимум
Совместное решение этих уравнений дает
Среднеквадратичные ошибки определения a и b равны
При обработке результатов измерения этим методом удобно все данные сводить в таблицу, в которой предварительно подсчитываются все суммы, входящие в формулы (19)–(24). Формы этих таблиц приведены в рассматриваемых ниже примерах. Пример 1. Исследовалось основное уравнение динамики вращательного движения ε = M/J (прямая, проходящая через начало координат). При различных значениях момента M измерялось угловое ускорение ε некоторого тела. Требуется определить момент инерции этого тела. Результаты измерений момента силы и углового ускорения занесены во второй и третий столбцы таблицы 7. Таблица 7
По формуле (19) определяем:
Отсюда
Для определения среднеквадратичной ошибки воспользуемся формулой (20)
= 0.005775 кг-1 · м-2 . По формуле (18) имеем
SJ = (2.996 · 0.005775)/0.3337 = 0.05185 кг · м2. Задавшись надежностью P = 0.95 , по таблице коэффициентов Стьюдента для n = 5, находим t = 2.78 и определяем абсолютную ошибку ΔJ = 2.78 · 0.05185 = 0.1441 ≈ 0.2 кг · м2. Результаты запишем в виде: J = (3.0 ± 0.2) кг · м2;
Пример 2. Вычислим температурный коэффициент сопротивления металла по методу наименьших квадратов. Сопротивление зависит от температуры по линейному закону Rt = R0(1 + α t°) = R0 + R0 α t°. Свободный член определяет сопротивление R0 при температуре 0°C, а угловой коэффициент – произведение температурного коэффициента α на сопротивление R0. Результаты измерений и расчетов приведены в таблице (см. таблицу 8). Таблица 8
По формулам (21), (22) определяем
R0 = ¯R- α R0¯ t = 1.4005 - 0.002645 · 85.83333 = 1.1735 Ом . Отсюда:
Найдем ошибку в определении
α. Так как
Пользуясь формулами (23), (24) имеем
= 0.014126 Ом. Тогда
Задавшись надежностью P = 0.95, по таблице коэффициентов Стьюдента для n = 6, находим t = 2.57 и определяем абсолютную ошибку Δα = 2.57 · 0.000132 = 0.000338 град-1. α = (23 ± 4) · 10-4 град-1 при P = 0.95.
Пример 3. Требуется определить радиус кривизны линзы по кольцам Ньютона. Измерялись радиусы колец Ньютона rm и определялись номера этих колец m. Радиусы колец Ньютона связаны с радиусом кривизны линзы R и номером кольца уравнением r2m = mλR - 2d0R, где d0 – толщина зазора между линзой и плоскопараллельной пластинкой (или деформация линзы), λ – длина волны падающего света. Пусть λ = (600 ± 6) нм; r2m = y; m = x; λR = b; -2d0R = a, тогда уравнение примет вид y = a + bx. Результаты измерений и вычислений занесены в таблицу 9. Таблица 9
Рассчитываем: 1. a и b по формулам (21), (22).
a = ¯ r2 - b¯m = (0.208548333 - 0.0594957 · 3.5) = 0.0003133 мм2. 2. Рассчитаем среднеквадратичные ошибки для величин b и a по формулам (23), (24)
3. При надежности P = 0.95 по таблице коэффициентов Стьюдента для n = 6 находим t = 2.57 и определяем абсолютные ошибки Δb = 2.57 · 0.000211179 = 6·10-4 мм2; Δa = 2.57 · 0.000822424 = 3· 10-3 мм2. 4. Записываем результаты b = (595 ± 6)·10-4 мм2 при Р = 0.95; a = (0.3 ± 3)·10-3 мм2 при Р = 0.95; Из полученных результатов опыта следует, что в пределах ошибки этого опыта прямая r2m = ƒ(m) проходит через начало координат, т.к. если ошибка значения какого-либо параметра окажется сравнимой или превысит значение параметра, то это означает, что скорей всего, настоящее значение этого параметра равно нулю. В условиях данного эксперимента величина a не представляет интереса. Поэтому мы ею больше заниматься не будем. 5. Подсчитаем радиус кривизны линзы: R = b / λ = 594.5 / 6 = 99.1 мм. 6. Так как для длины волны дана систематическая ошибка, подсчитаем и для R систематическую ошибку по формуле (16), взяв в качестве систематической ошибки величины b ее случайную ошибку Δb.
Записываем окончательный результат R = (99 ± 2) мм ε ≈ 3% при P = 0.95. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 7. Вычисления
Цель эксперимента – получить некоторую числовую величину, и поэтому точность при вычислениях также важна, как и при измерениях. Ведь ошибка в вычислениях может свести насмарку прекрасно задуманный и умело осуществленный эксперимент. У студентов иногда возникает ложное представление, что числовые выкладки – это тривиальное и не очень важное дело. И неспособность к ним даже говорит о наличии математического таланта. Существует и другая точка зрения, – что ошибки в расчетах происходят независимо от воли людей. По этому поводу заметим, что хотя никто не застрахован от ошибки, во-первых, при рациональном подходе к вычислениям можно уменьшить вероятность их появления и, во-вторых, от нее есть средство, а именно проверка вычислений. Рассмотрим эти вопросы. Способы борьбы с арифметическими ошибками.
Пример:
Допустим, что вы исследуете зависимость
средней арифметической скорости
молекул от температуры,
Н
В этом случае мы имеем дело с несамопроверающимися вычислениями. Если вы работаете с напарником, то лучше каждому из вас произвести расчет самостоятельно. Если оба результата согласуются, то почти наверняка оба верны. Если вы работаете один, то надо постараться привести проверки выкладок другим способом. Некоторые могут подумать, что вычислять результат двумя способами – излишняя предосторожность. Но ошибки вычислений – главная причина того, что экспериментатору приходится понапрасну тратить время. Тщательная же проверка в итоге приводит к сбережению времени. Помните, что если в учебной лаборатории кто-то может проверить вашу работу и найти ошибки, то потом уже никто не сделает этого. Вы должны выработать у себя привычку при вычислениях всегда прикидывать результат в уме хотя бы с точностью 30% Например, в случае выражения (25) следует прикинуть в уме примерно так:
Значит, z ≈ 4000. Если при проверке получен результат, не согласующийся с первоначальным, то сначала пересмотрите ход проверочного расчета, ибо он наверняка проводился менее аккуратно. Рассказывают, что один новенький аспирант–теоретик как-то принес показать результаты сложных расчетов своему руководителю, известному физику. Проглядев их, руководитель сказал: «Если взять следующий частный случай, то ваш результат должен свестись к тому-то и тому». Он набросал на обложке две строчки выкладок и сказал: «Видите, не получается. Вы где-то ошиблись». Смущенный аспирант забрал работу и потратил целый месяц, чтобы повторить все заново. Потом снова пришел к руководителю. – Ну, как, – спросил именитый ученый, – нашли ошибку? – Да, – ответил тот, – в двух строчках ваших выкладок. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 8. О написании вывода
Не зря говорят, что конец – всему делу венец. Вывод по работе должен логически завершить ее. Многие студенты, как правило, затрудняются сформулировать вывод, не знают, что же им писать, и в итоге появляются однообразные фразы – «в результате работы мы получили то-то и то-то», – и все, на этом вывод заканчивается. На что же нужно обратить внимание при написании вывода? Главное внимание должно быть обращено на анализ результатов. Здесь нужно провести:
Нужно выяснить – надежно ли подтверждают полученные вами результаты выводы теории, в чем причина возможных отклонений. Сравнивая результаты с данными таблиц и результатами товарищей, не следует при несовпадении сразу считать свои данные ошибочными. Нужно тщательно продумать методику измерений, стараясь вскрыть расхождения. Может быть, это влияние отдельных теоретических упрощений; или недостатки данной методики измерения (предложите другую); или велики приборные погрешности используемой аппаратуры (какие именно?); или сказалось влияние каких-либо внешних факторов (что именно?) и т.д. Обратитесь к книгам, обсудите вопрос с напарником, поразмышляйте, а потом изложите итог ваших размышлений в выводе. При сдаче работы с «плохими» результатами вы, после обсуждения с преподавателем, можете получить значительно больше пользы, чем при наличии «хороших» результатов. Отметим еще отдельные моменты.
Последнее слово здесь пусть скажет не физик, а – великий Сервантес: «Старайтесь вразумительно выражать свои Мысли и выставлять их в самом правильном свете, работая как можно больше над тем, чтобы не оставлять их темными и запутанными, а сделать ясными и понятными». |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Использованная литература
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

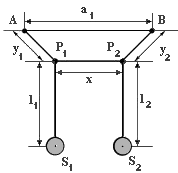
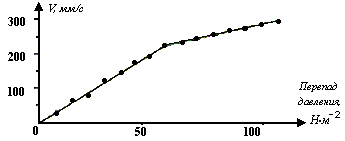
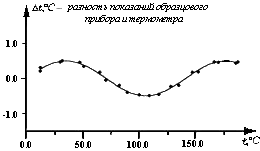
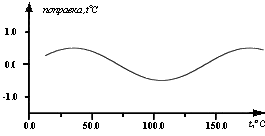
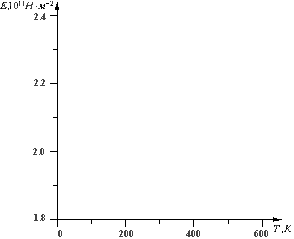 Рис.7.
Зависимость модуля Юнга от температуры
Т.
Рис.7.
Зависимость модуля Юнга от температуры
Т.

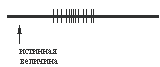
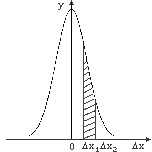
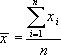 ,
(5)
,
(5) .
(6)
.
(6)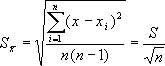 .
(8)
.
(8)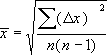
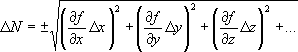 (17) или
(17) или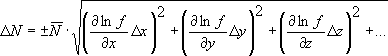 ,
(18)
,
(18)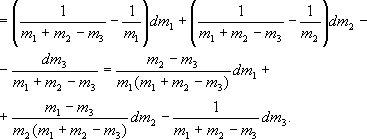 .
.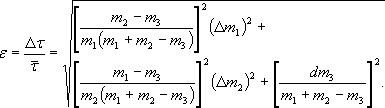 .
.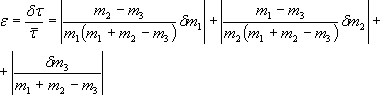 .
.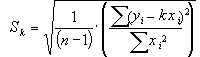 ,
(20)
,
(20)
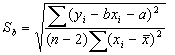 (23)
(23)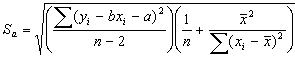 . (24)
. (24)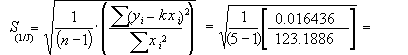
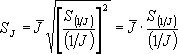 .
. ,
,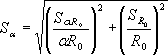 .
.
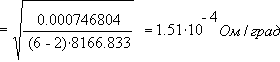 ;
;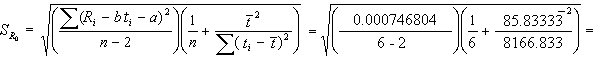
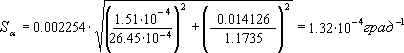 .
.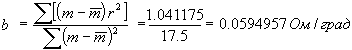 ;
;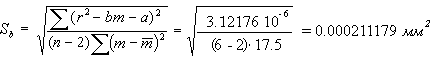 ;
;