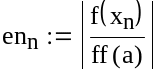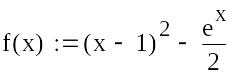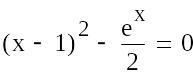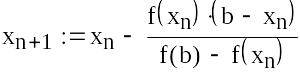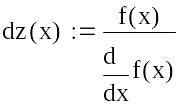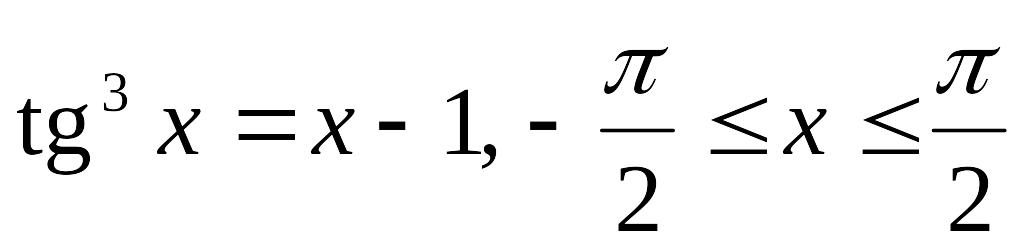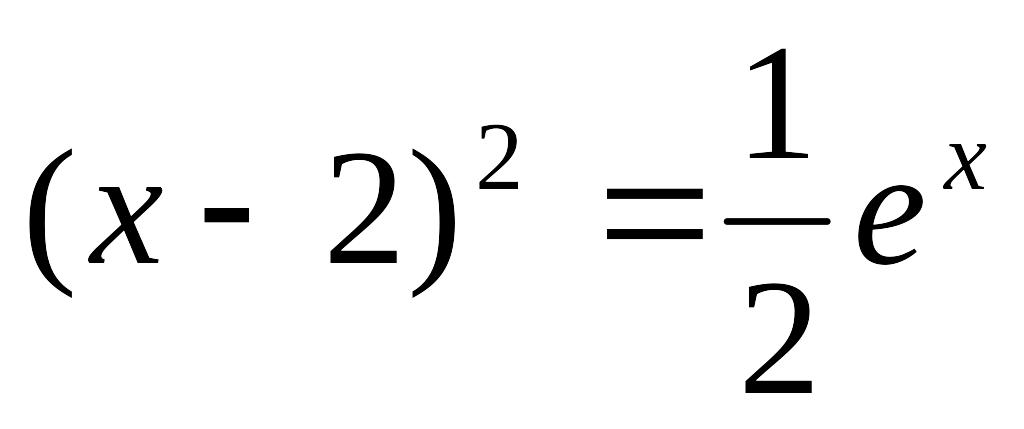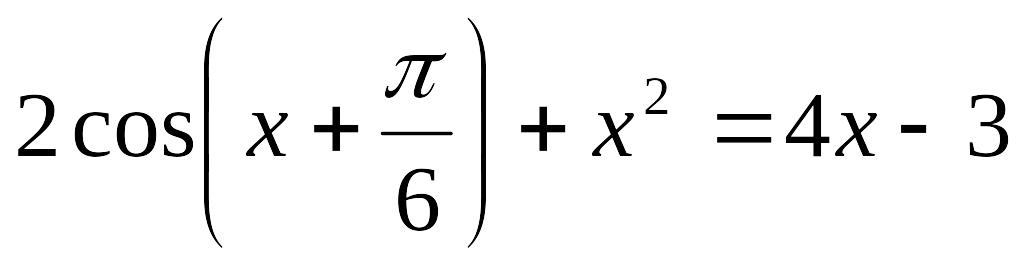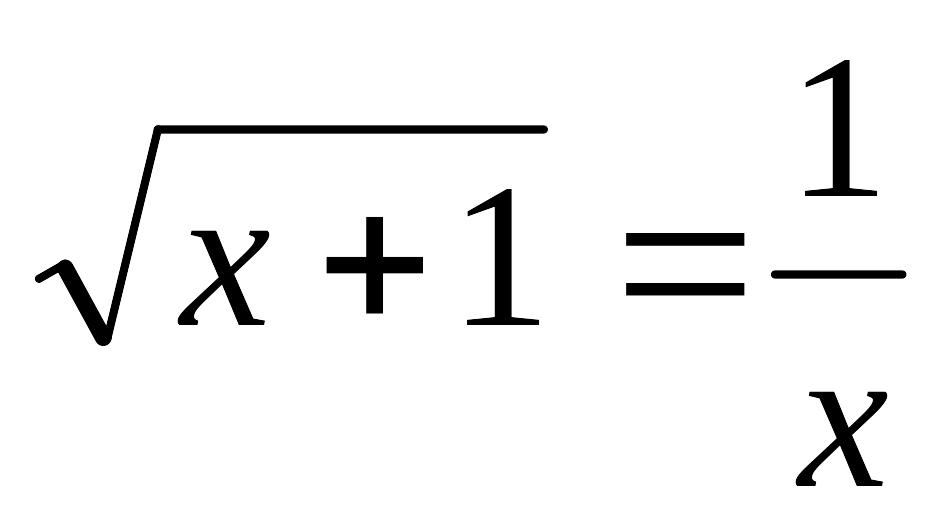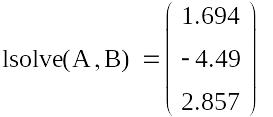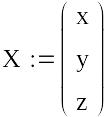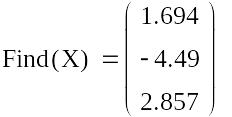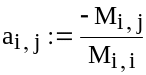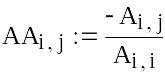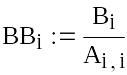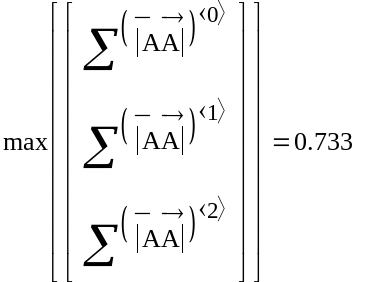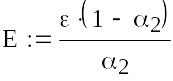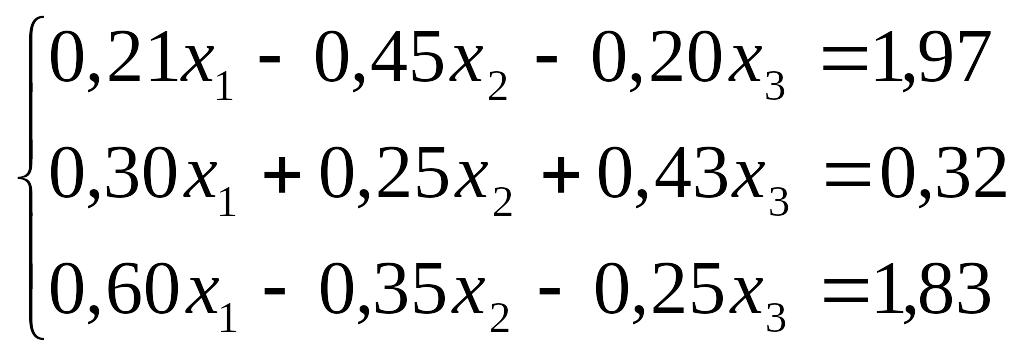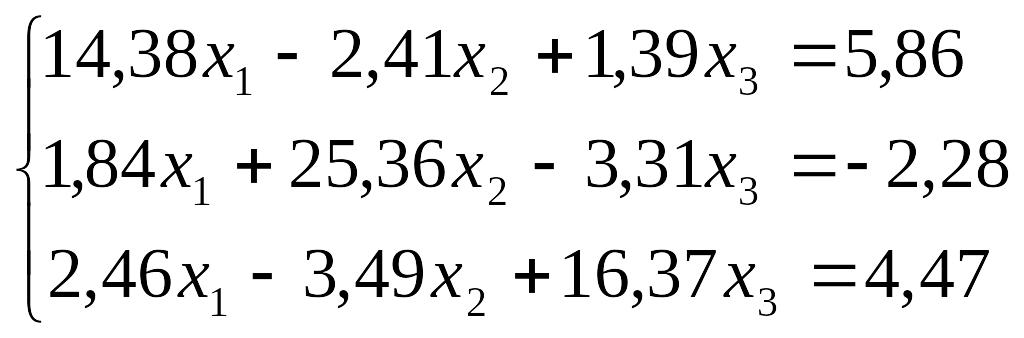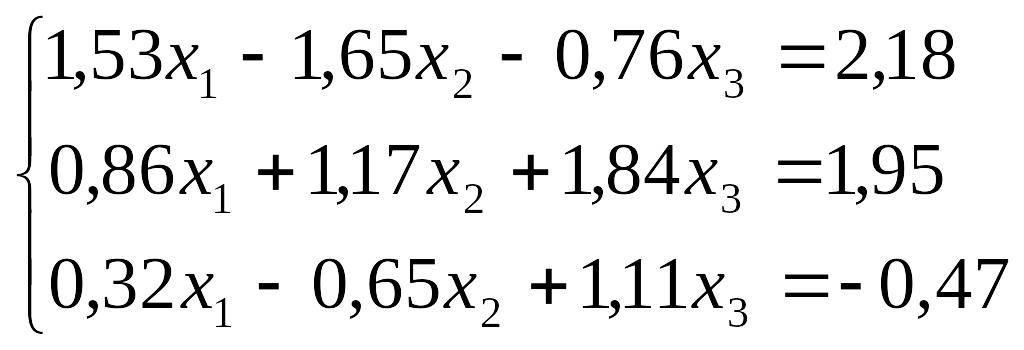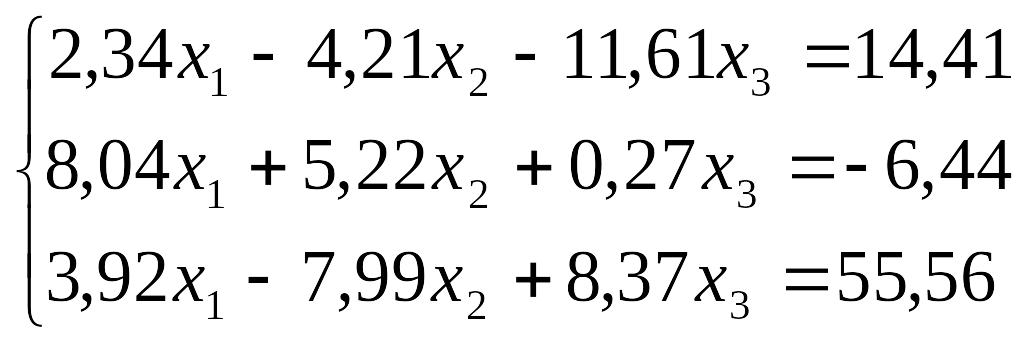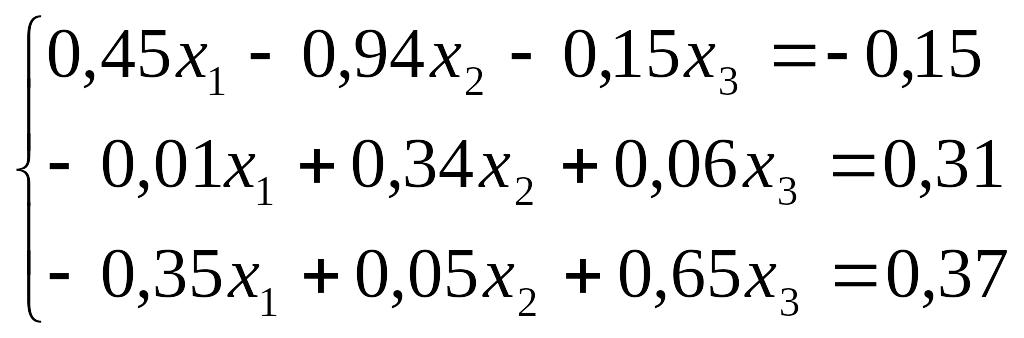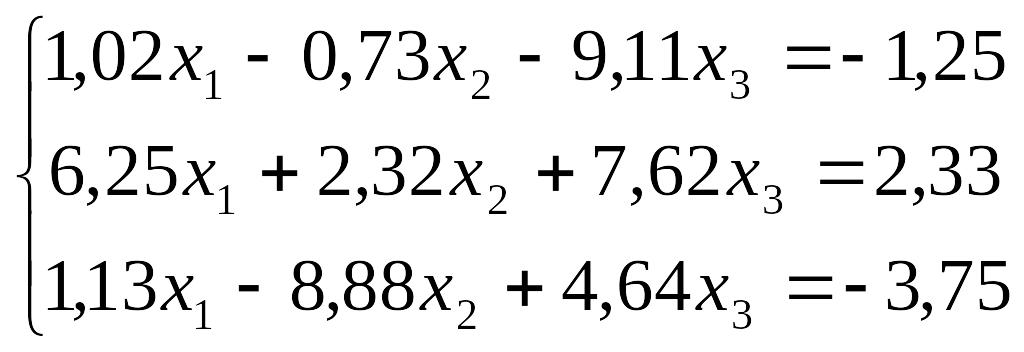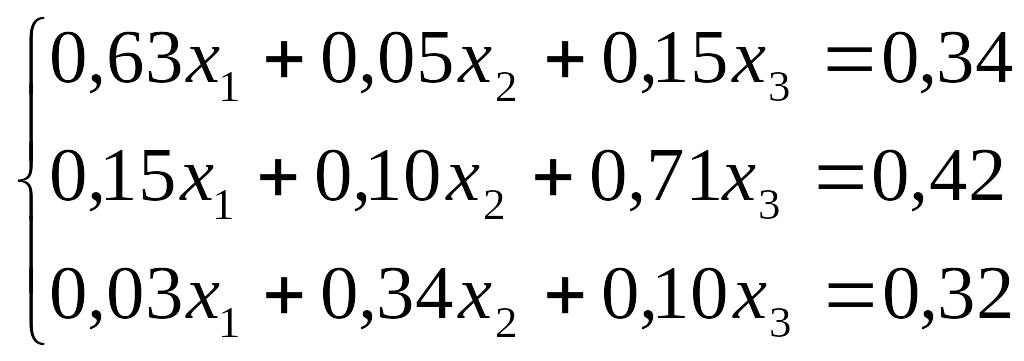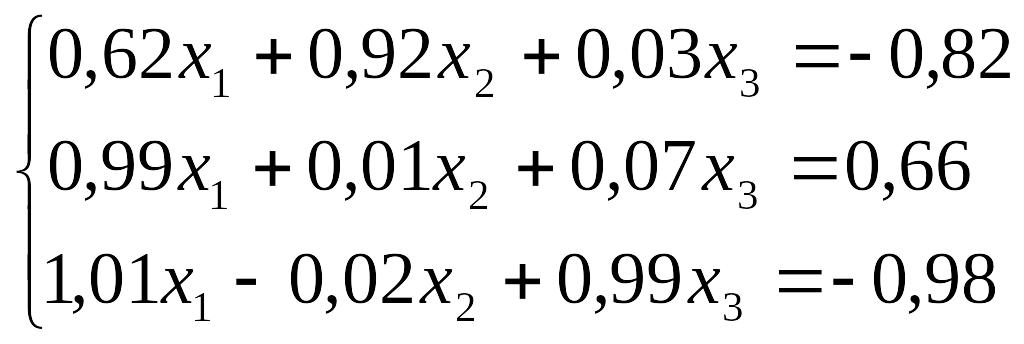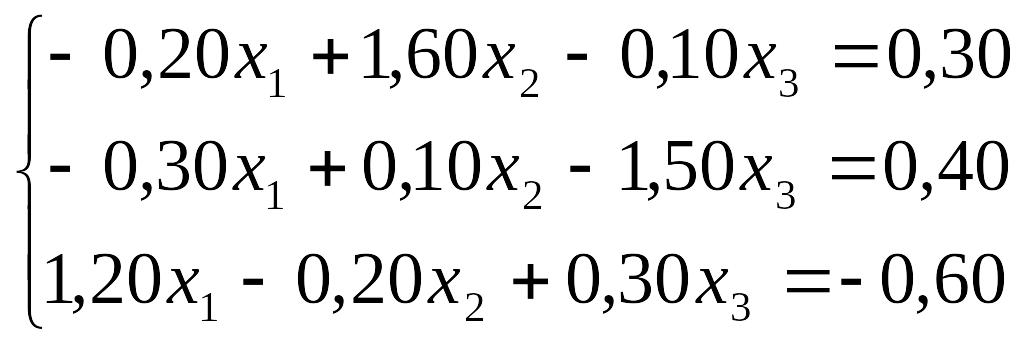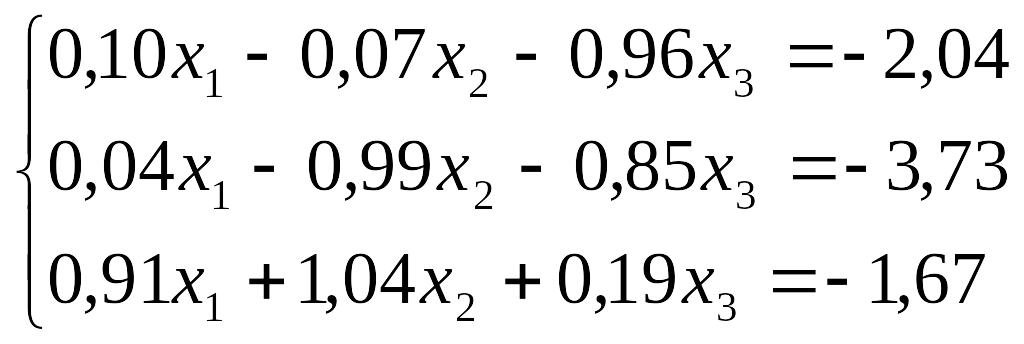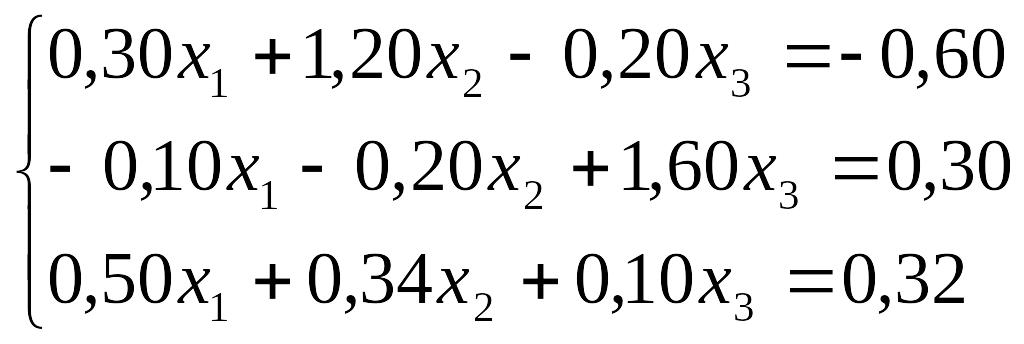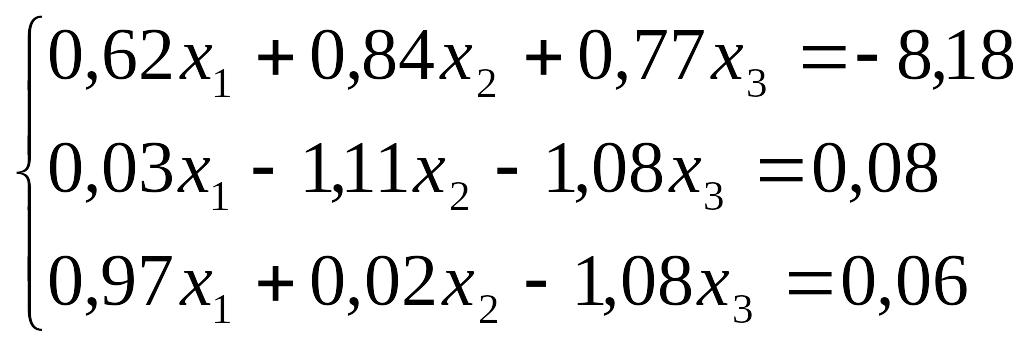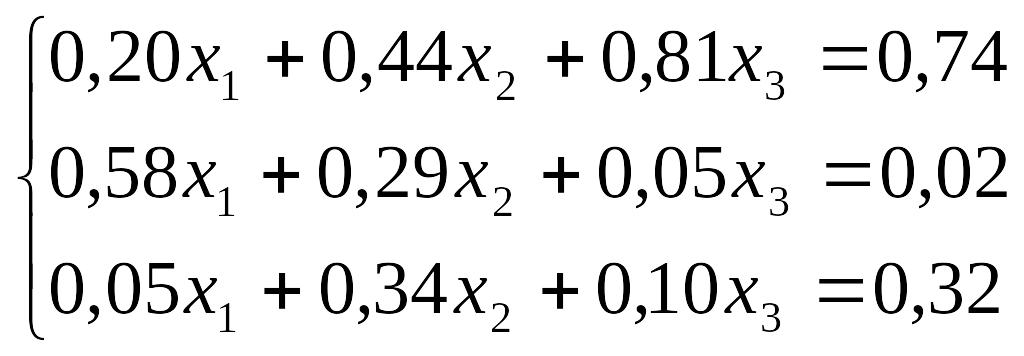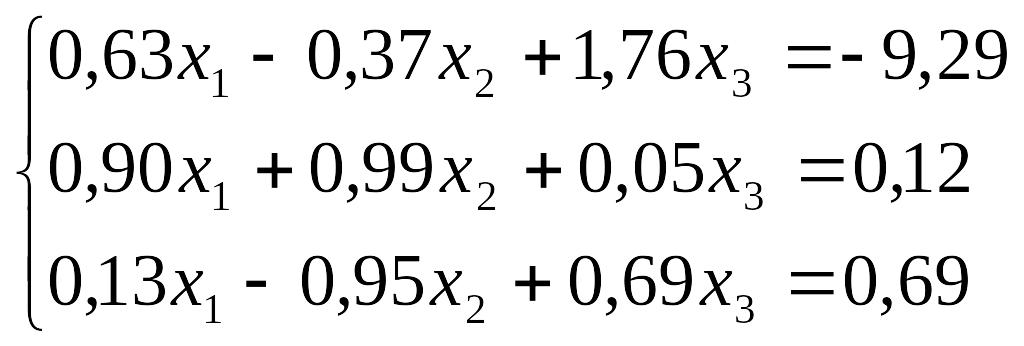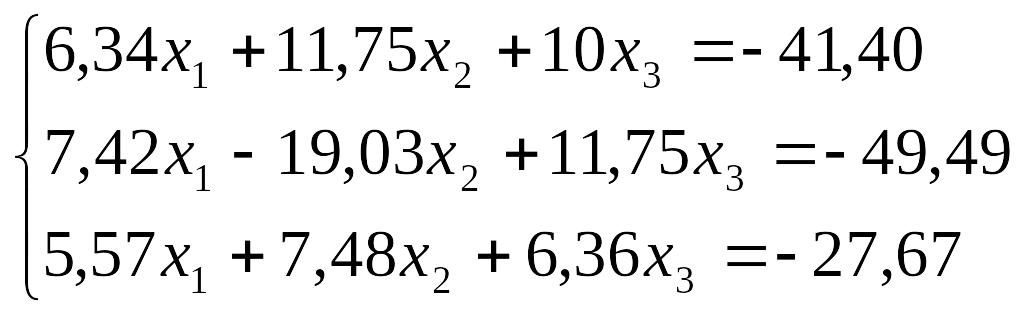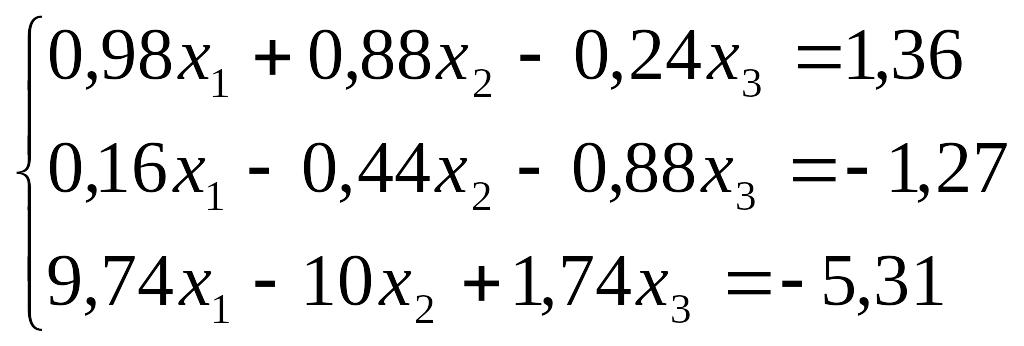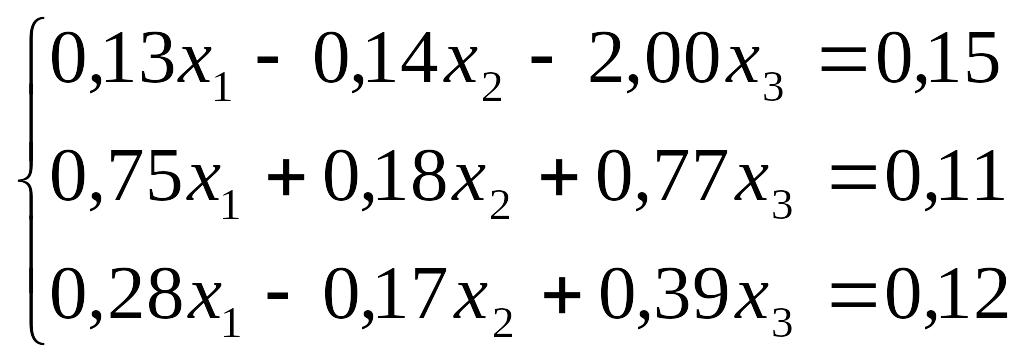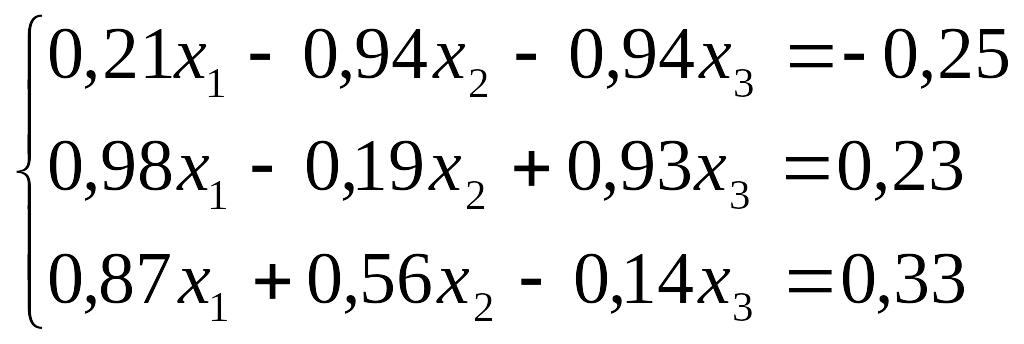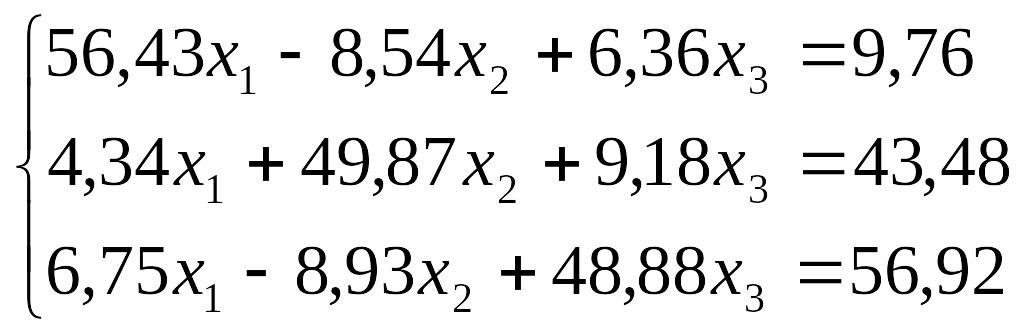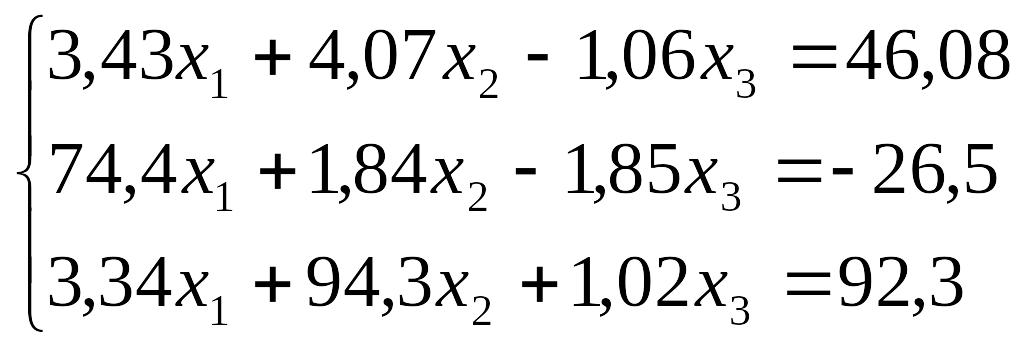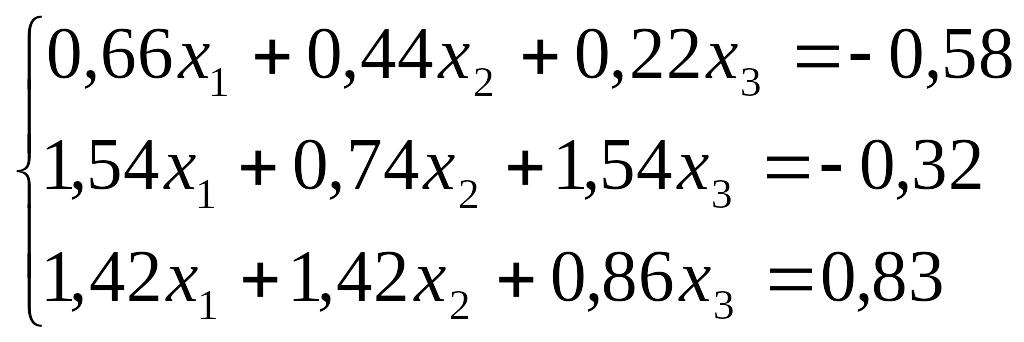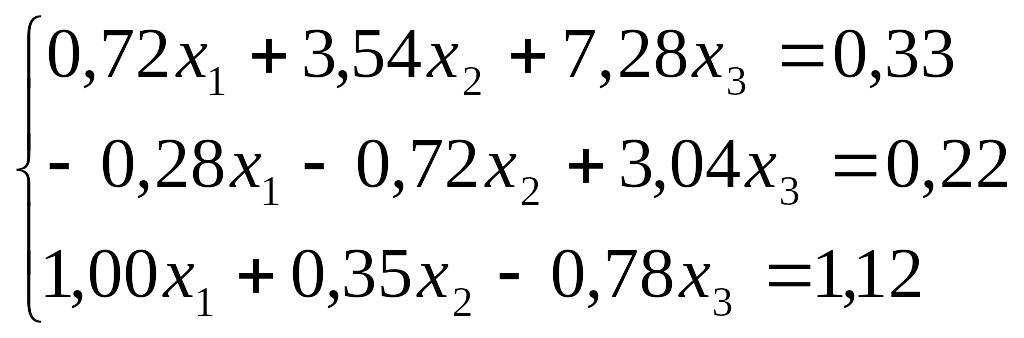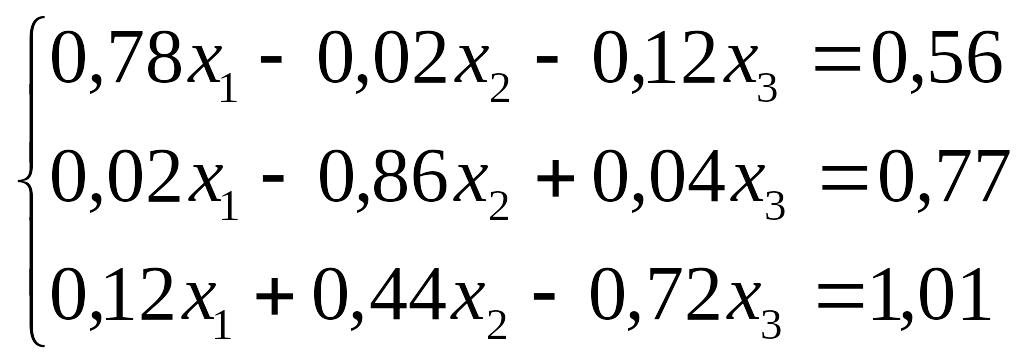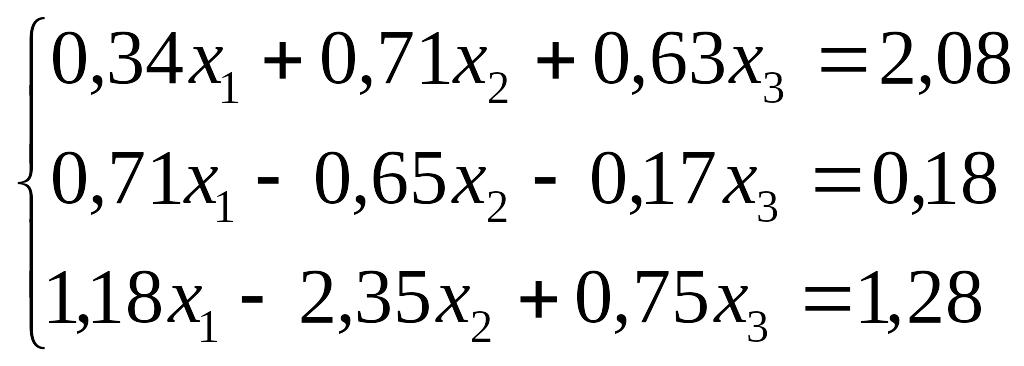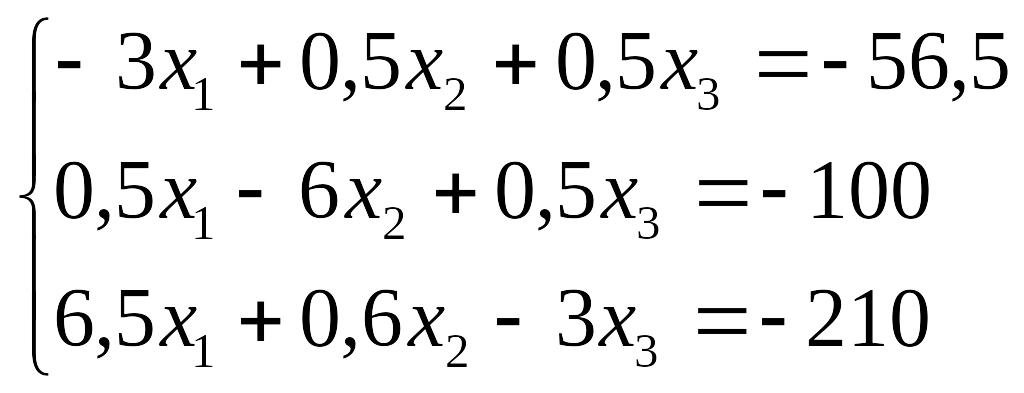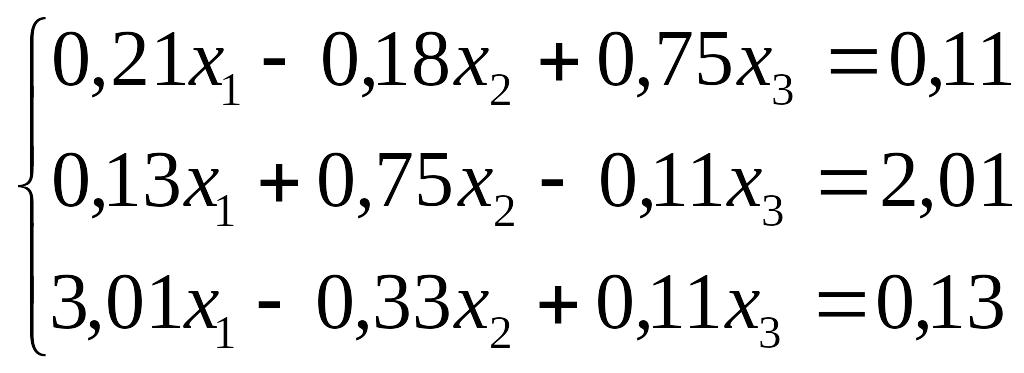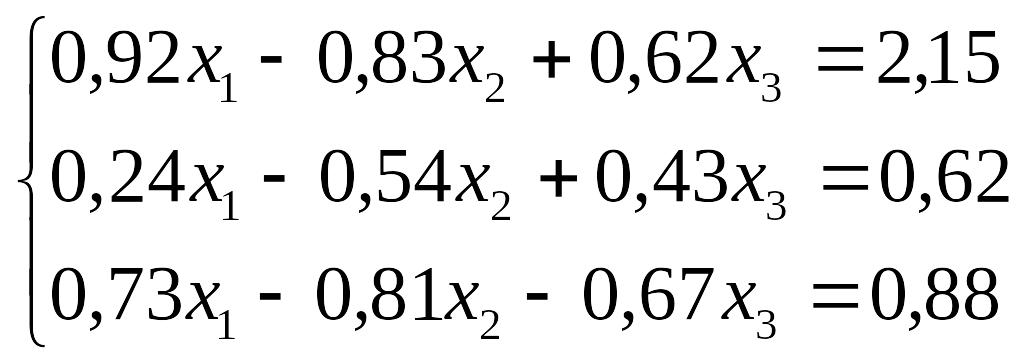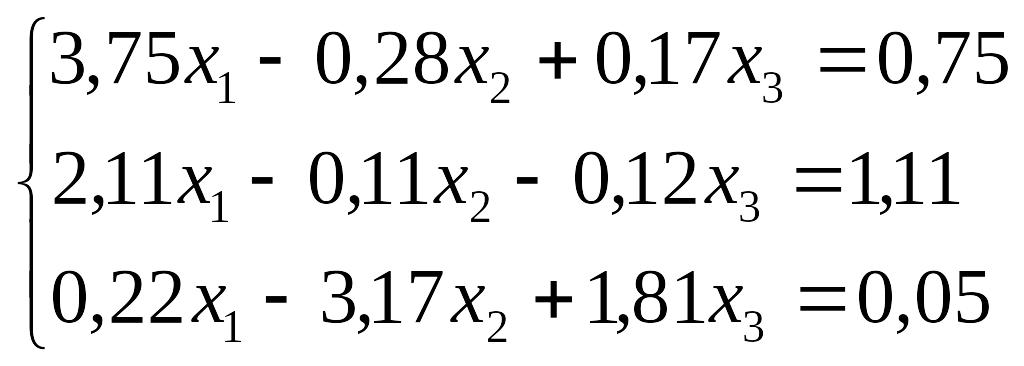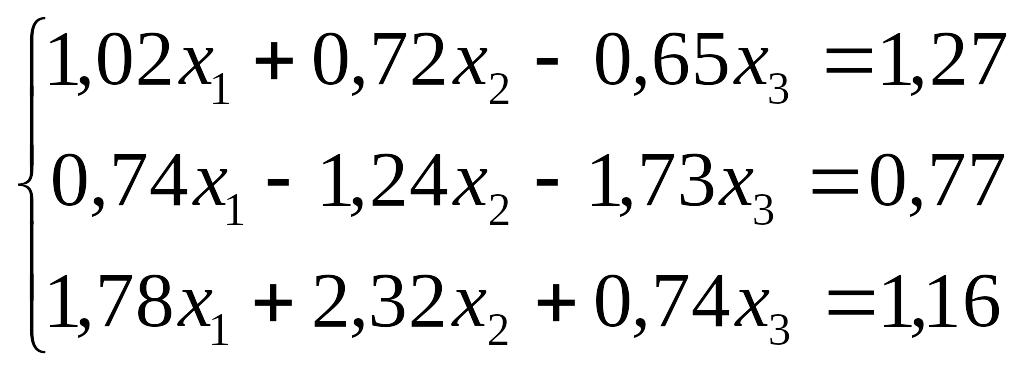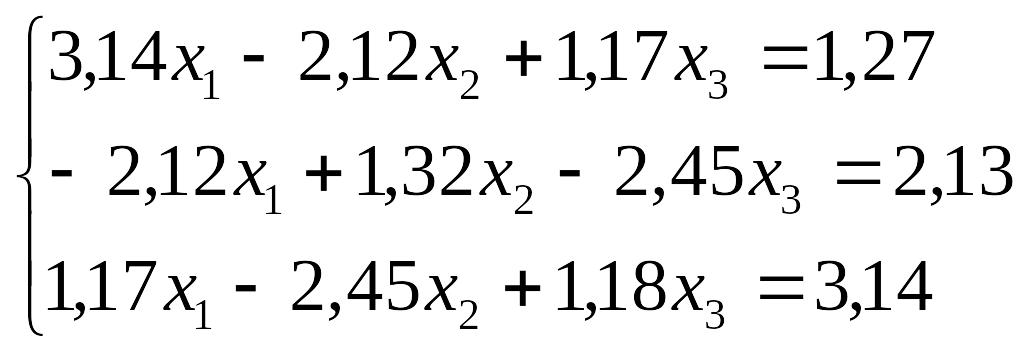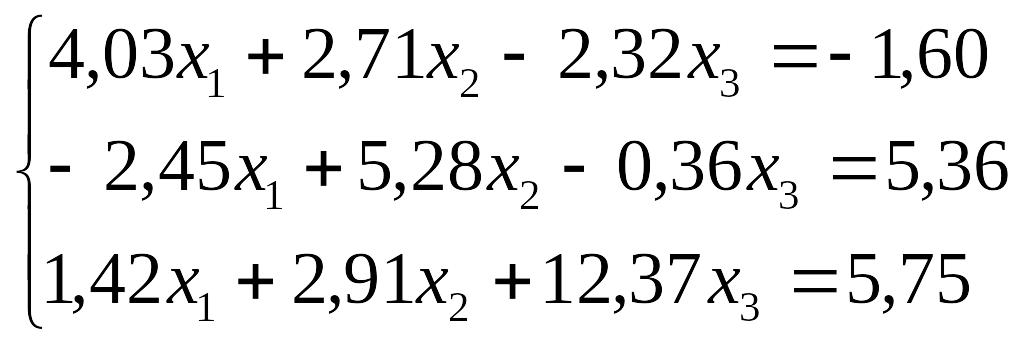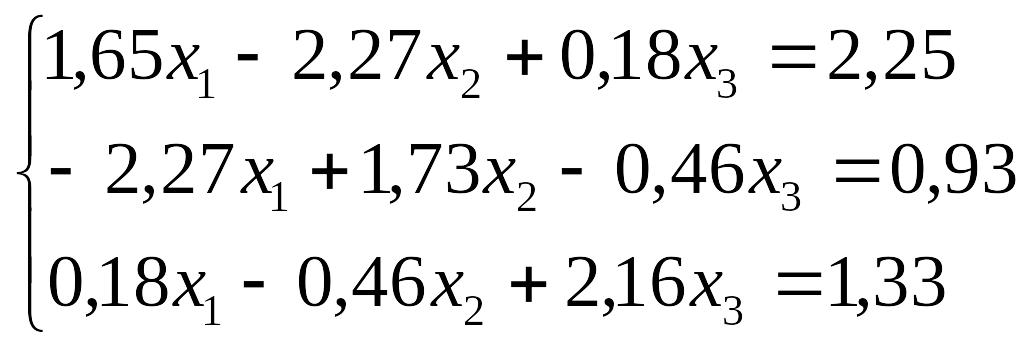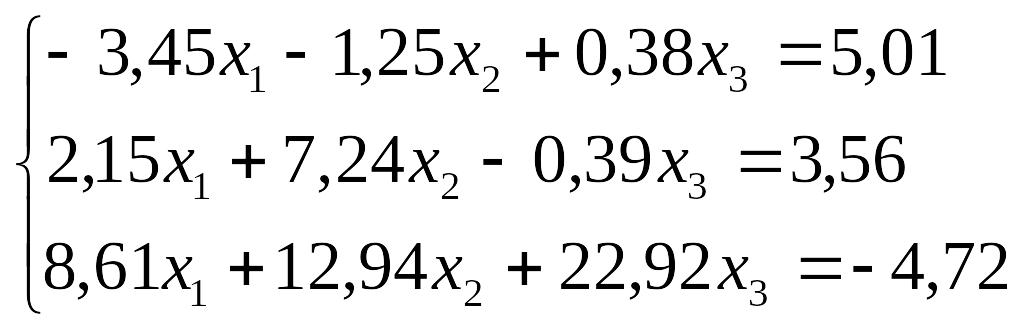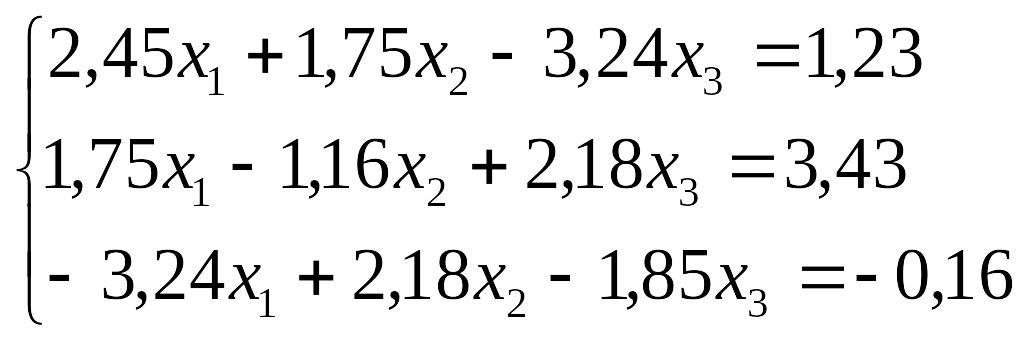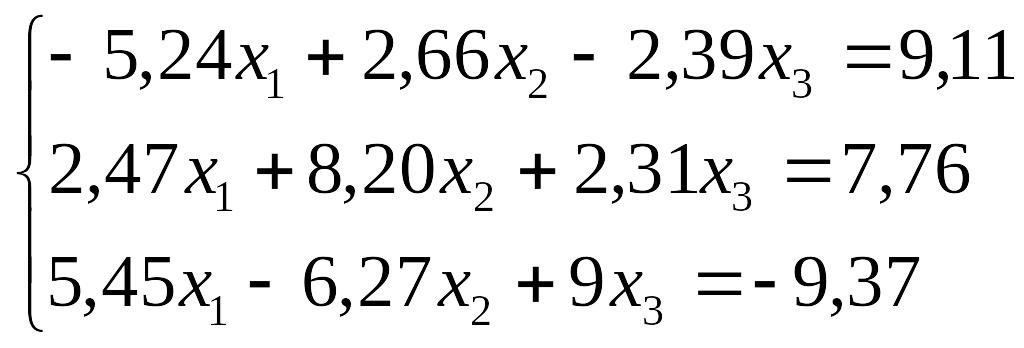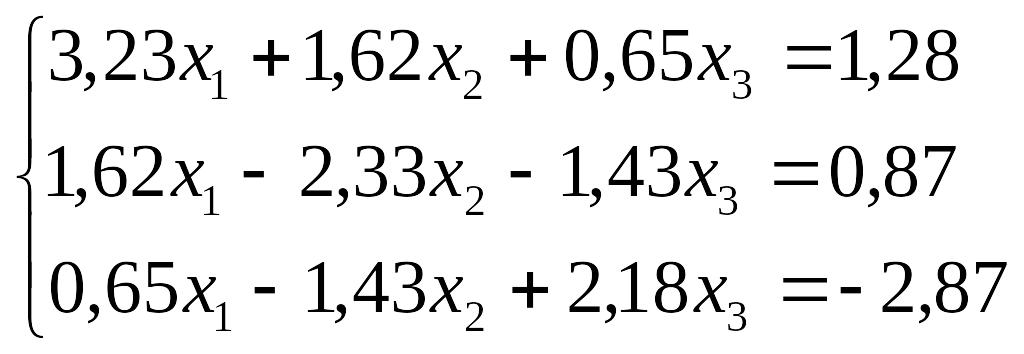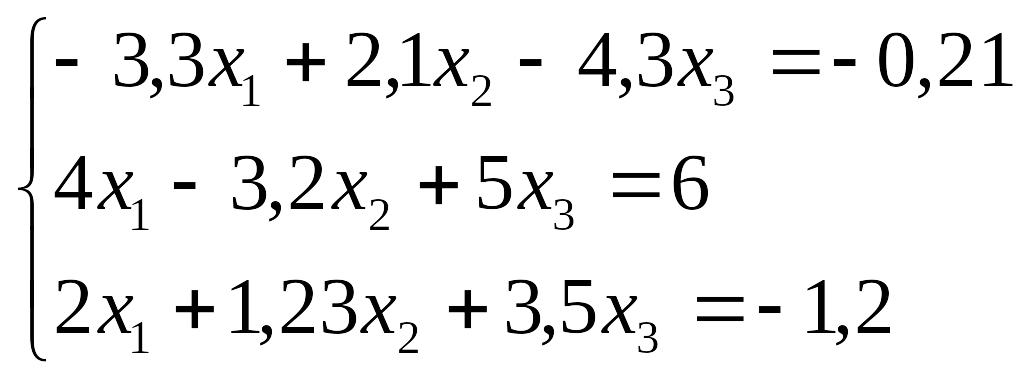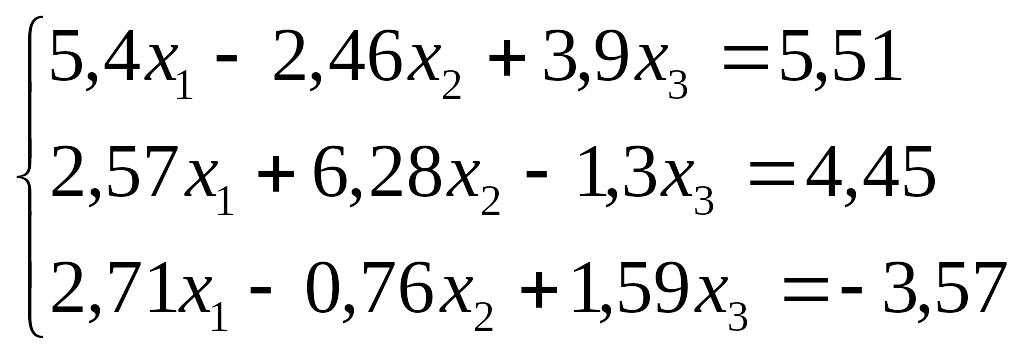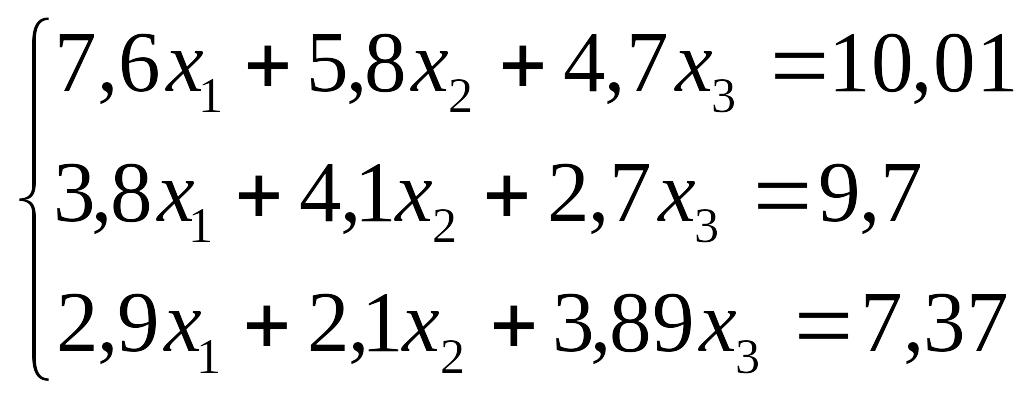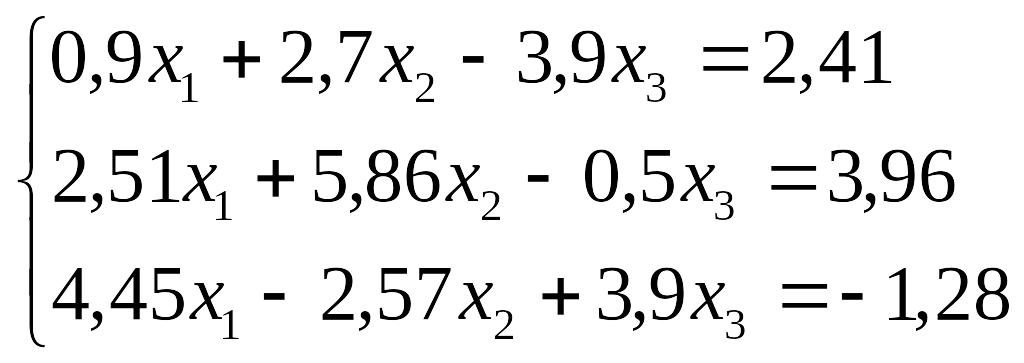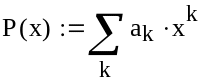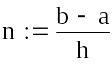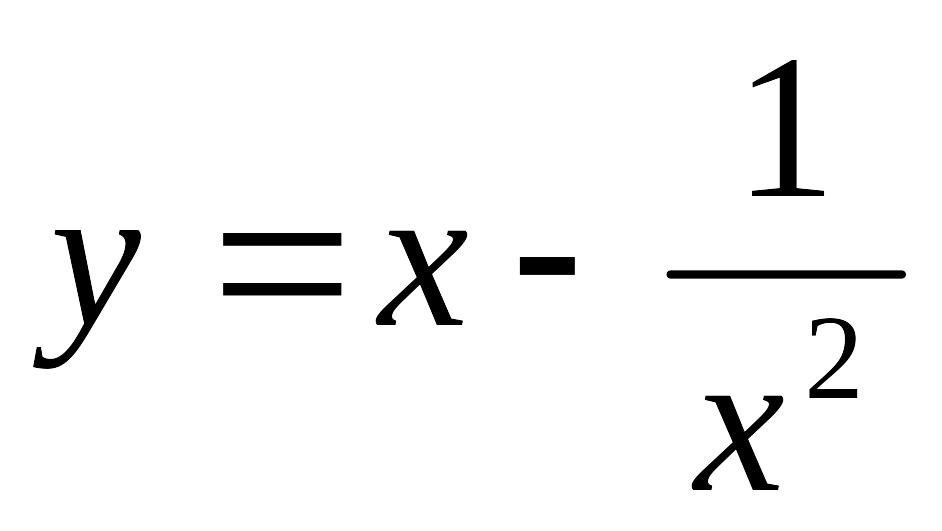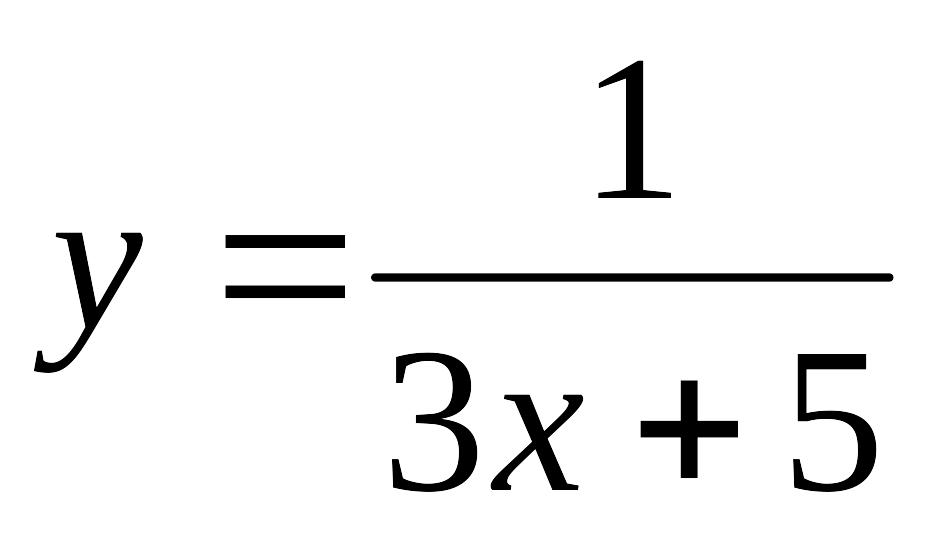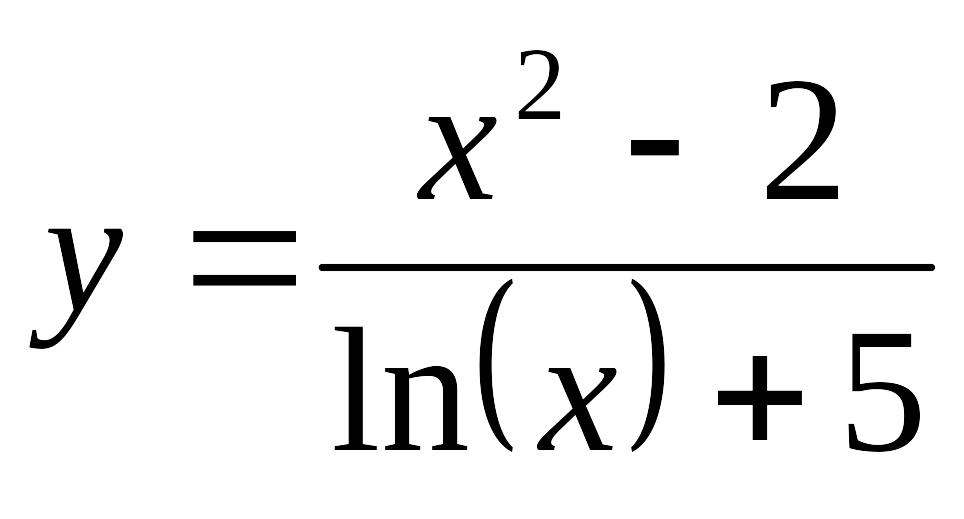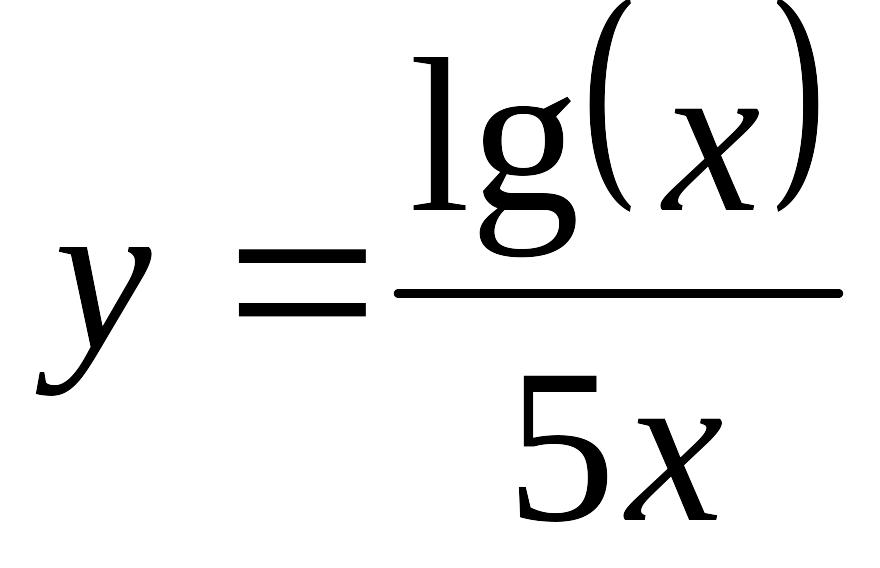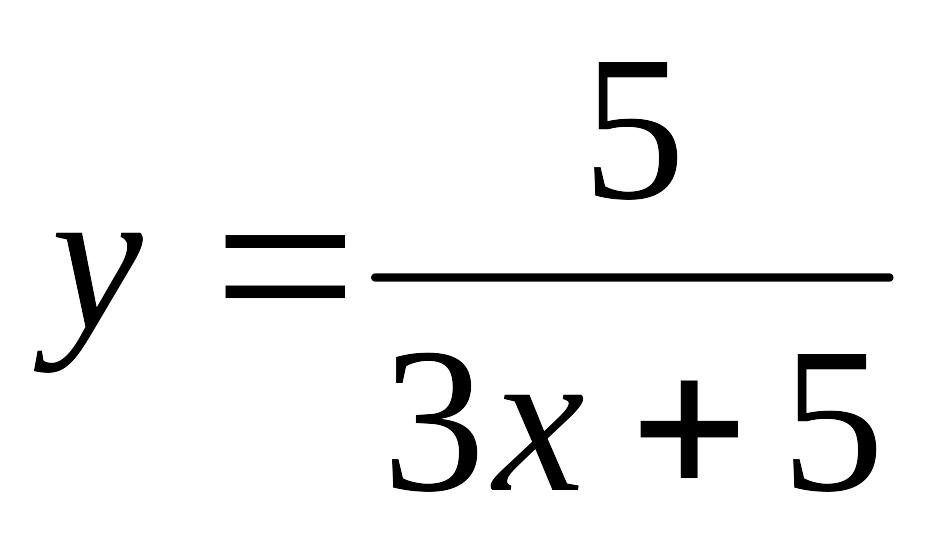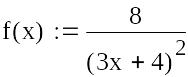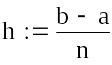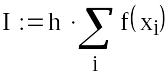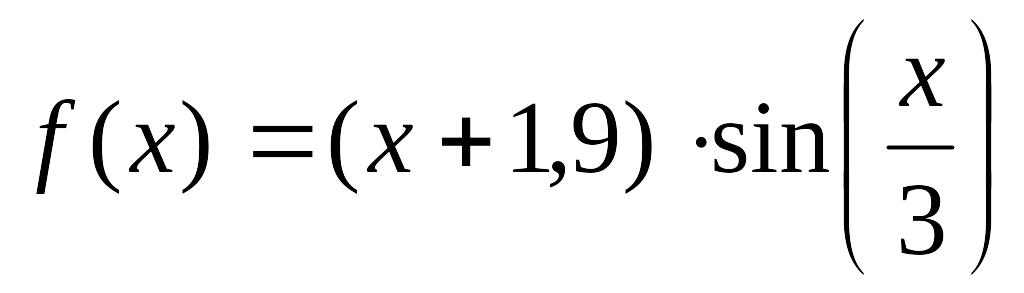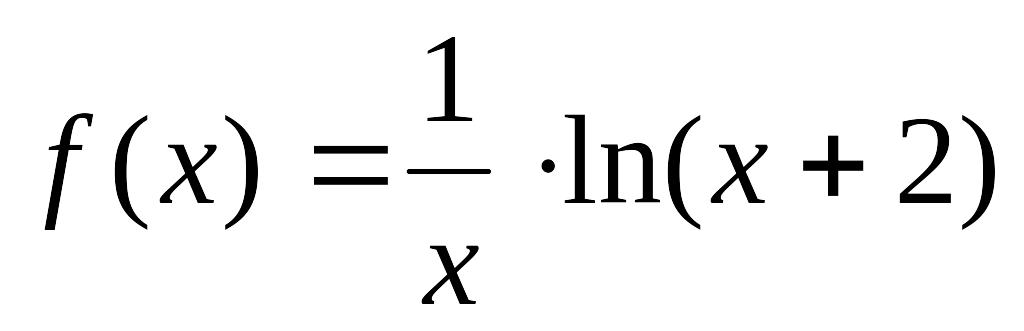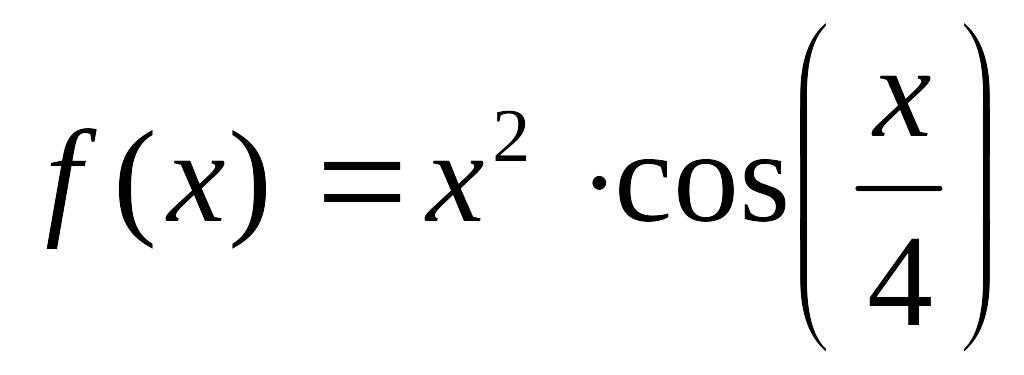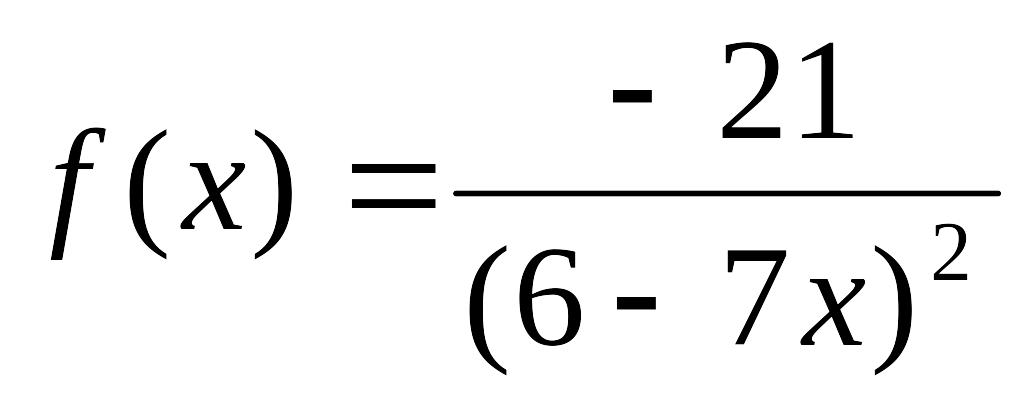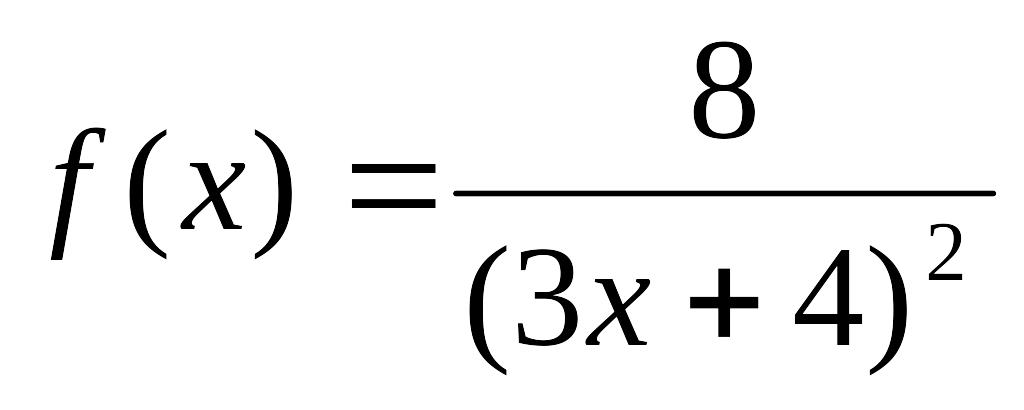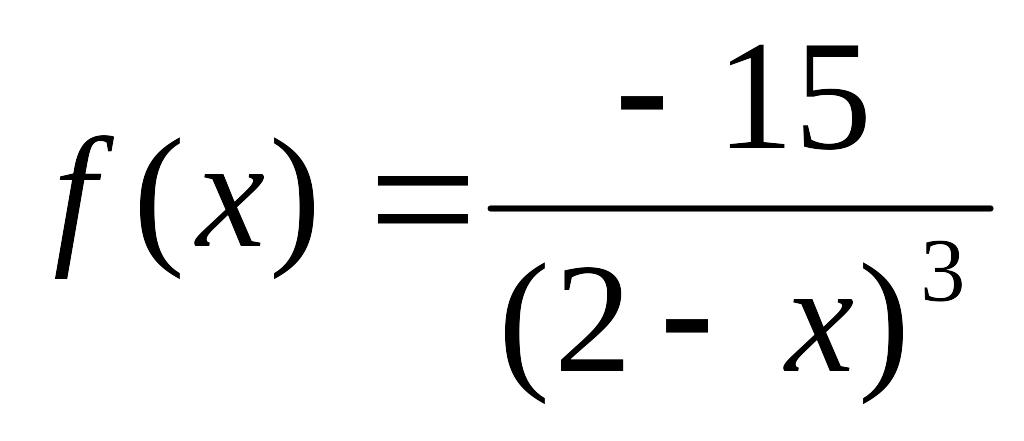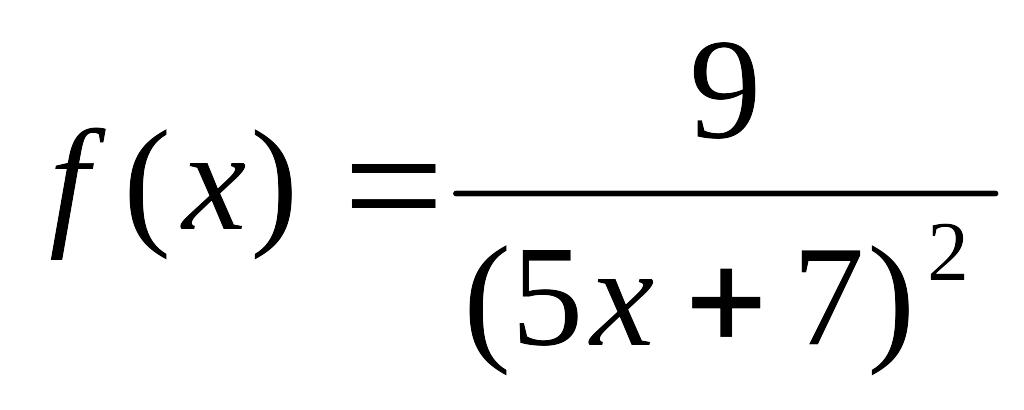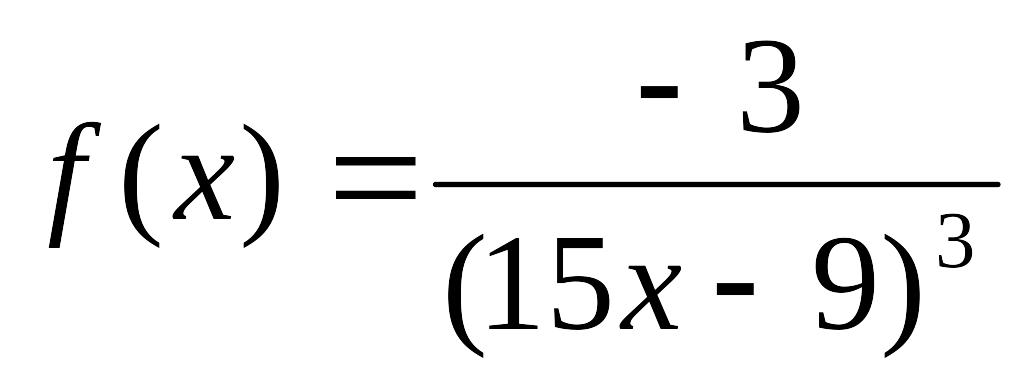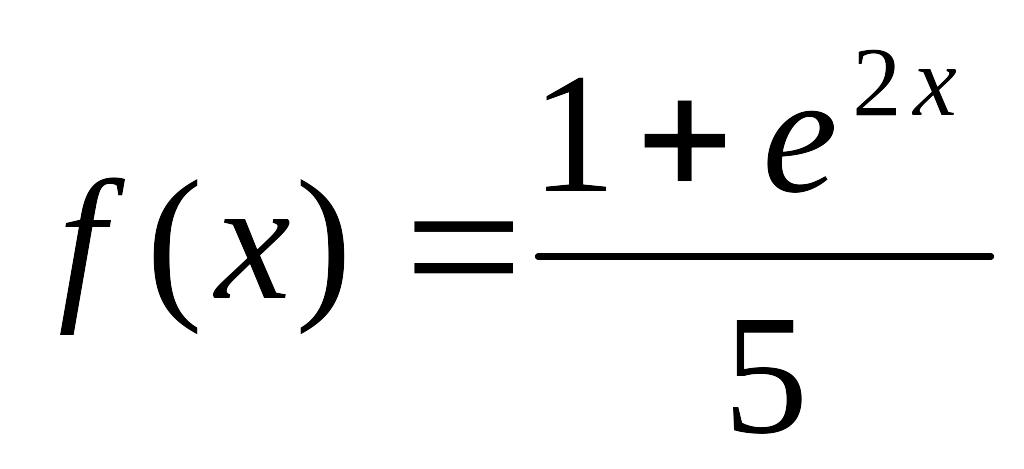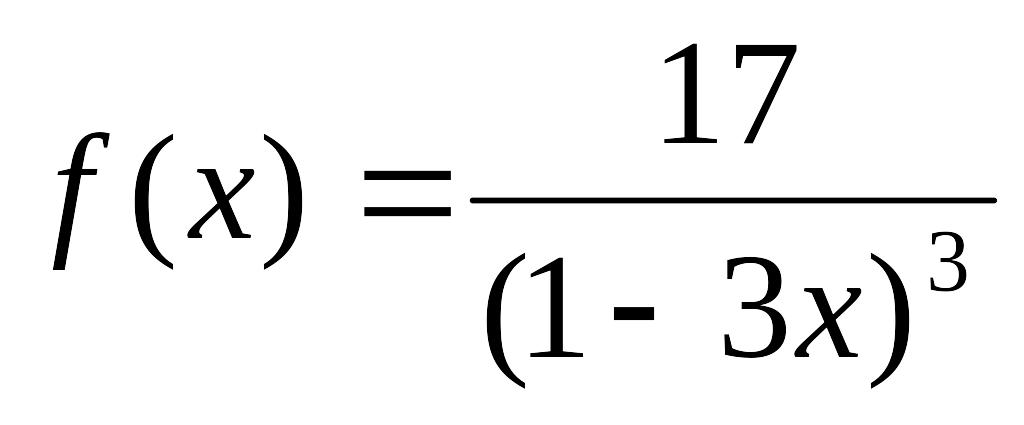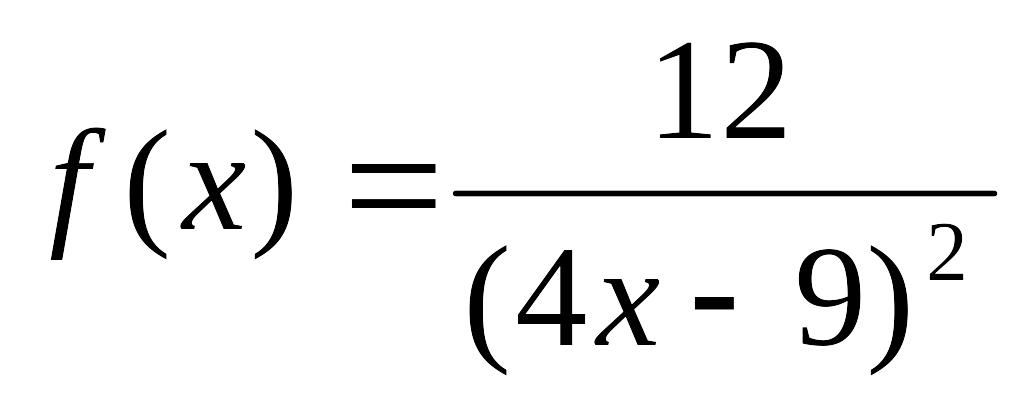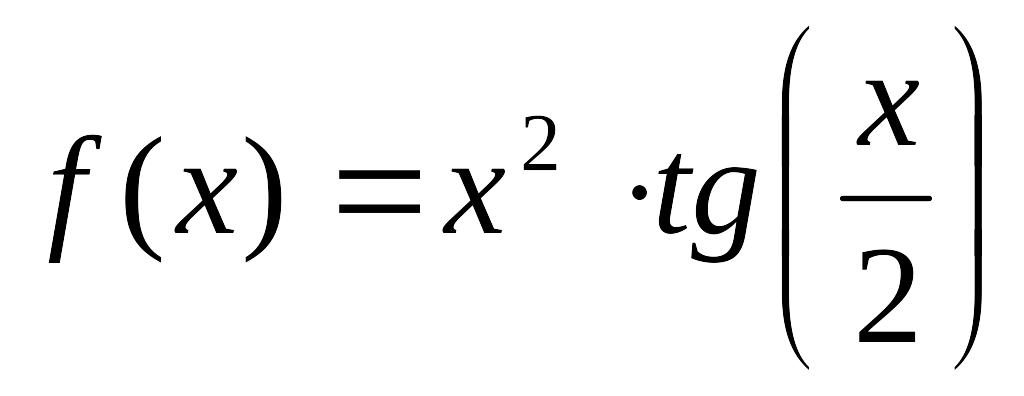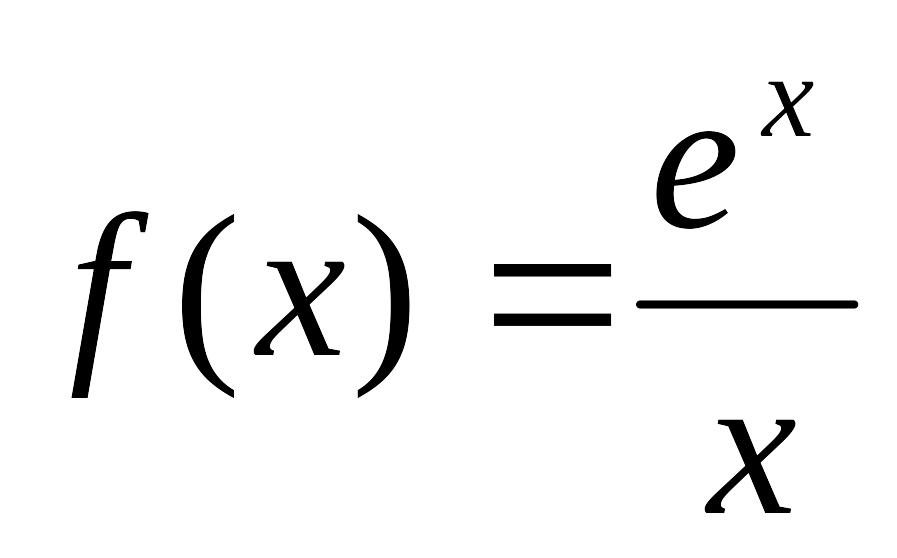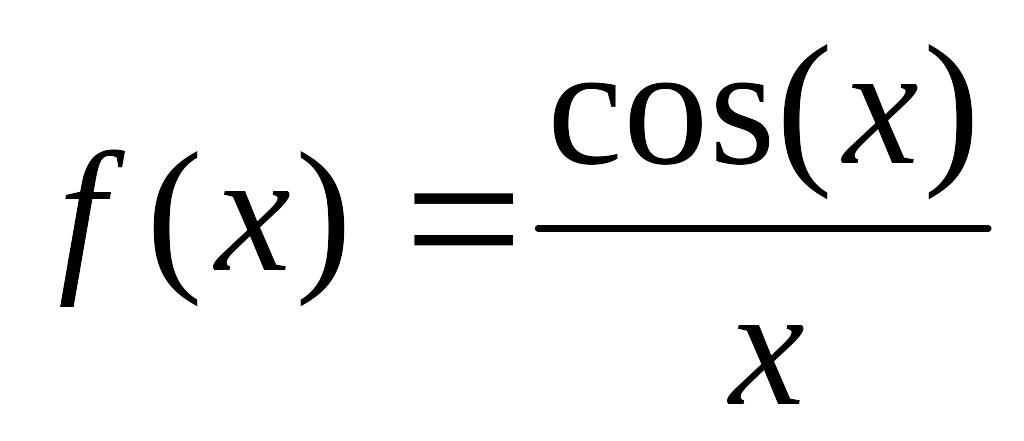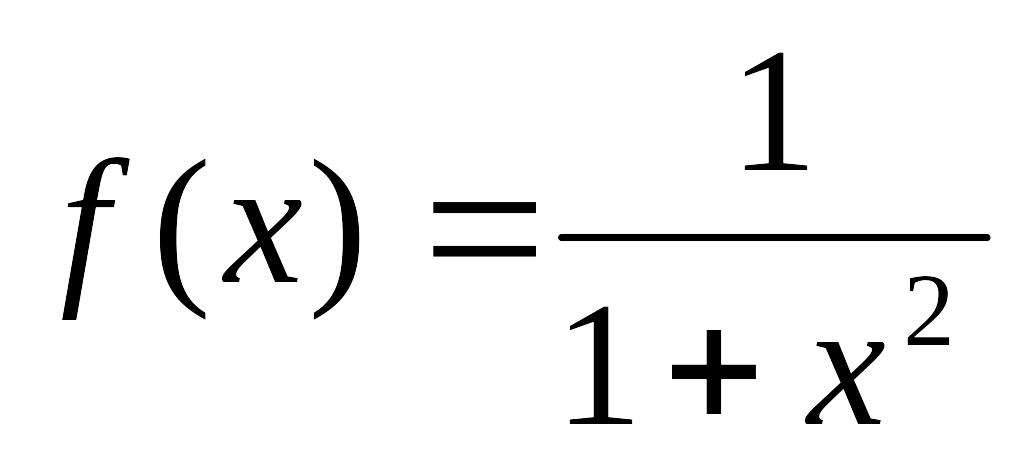Побудова пересічних фігур

Особливим інтересом є можливість побудови на одному графіку ряду різних фігур або поверхонь з автоматичним обліком їх взаємного перетину. Для цього треба роздільно задати матриці відповідних поверхонь і після виведення шаблону 3D-графика перерахувати ці матриці під ним з використанням як роздільник коми (рис. 4).

Порядок виконання лабораторної роботи 1

Вправа 1. Обчислити:

|-10| = 10! = .

Це і решту всіх завдань забезпечити коментарями, використовуючи команду

Вставка  Текстова область.

Вправа 2. Визначити змінні: а := 3.4, b := 6.22, з  0.149 (причому змінну з - глобально) і вирази:

.

• Обчислити вирази.

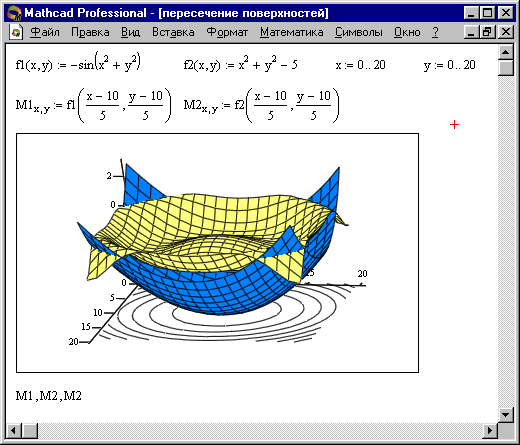
Рис. 4. Побудова двох пересічних поверхонь і одночасно контурного графіка однієї з них

• За допомогою команди Форматрезультатформат чиселЧисло знаків змінити точність відображення результатів обчислення глобально.

Вправа 3. Вивести на екран значення системної константи  і встановити максимальний формат її відображення локально.

Вправа 4. Виконати наступні операції з комплексними числами:

Z := -3 + 2i |Z| = Re(Z)= Im(Z)= arg(Z)=

= = 2  Z = Z1:= 1 + 2i Z2:= 3 + 4i

Z1 + Z2 = Z1 - Z2 = Z1 Z2 = Z1/Z2 =

Вправа 5. Виконати наступні операції:

i := 1 .. 10 = = = = x := 2 = =

Вправа 6. Визначити вектори d, S і R через дискретний аргумент i. Відобразити графічно табличний задані функції Si(di) і Ri(di), використовуючи команду Вставкаграфікx-y Залежність.

Щоб оформити графік, необхідно виконати наступні команди:

• Клацнути лівою клавішею миші на графіці, щоб виділити його. Потім клацнути правою клавішею миші, при цьому з'явиться контекстне меню в якому необхідно вибрати команду Формат (з'явиться діалогове вікно “Formatting Currently Selected X-Y Plot”).

• Нанести лінії сітки на графік (Осі X-Y Вспом. лінії) і відобразити легенду (Следськрить легенду)

• Відформатувати графік так, щоб в кожній вузловій точці графіка функції Si(di) стояв знак вигляду  (Следсимволbox), а графік функції Ri(di) відобразити у вигляді гістограми (Следтіпbar).

Вправа 7. Побудувати декартові (X-Y Залежність) і полярні

(Полярні Координати) графіки наступних функцій:

Для цього необхідно визначити  як дискретний аргумент на інтервалі від 0 до 2 з кроком /30.

Визначити по графіку X-Y Залежність координати будь-якій з точок перетину графіків Y() і P(), для цього необхідно:

• Виділити графік і вибрати з контекстного меню Масштаб (з'явиться діалогове вікно “X-Y Zoom”) для збільшення частини графіка в області точки перетину.

• На кресленні виділити пунктирним прямокутником околиця точки перетину графіків Y() і P(), яку потрібно збільшити.

• Натиснути кнопку Масштаб+, щоб перемальовувати графік.

• Щоб зробити це зображення постійним, вибрати ОК.

• Вибрати з контекстного меню Трасування (з'явиться діалогове вікно “X‑Y Trace”).

• Усередині креслення натиснути кнопку миші і перемістити покажчик миші на крапку, чиї координати потрібно побачити.

• Вибрати Copy X (або Copy Y), на вільному полі документа набрати Xper := (або Yper :=) і вибрати пункт меню Правкавставка.

Обчислити значення функцій Х() і Y() при :=2.

Вправа 8. Використовуючи команду Вставкаматріца створити матрицю Q розміром 66, заповнити її довільно і відобразити графічно за допомогою команди Вставкаграфікповерхності.

Вправа 9. Побудувати графік поверхні (Поверхні) і карту ліній рівня (Контурний) для функції два змінних

двома способами:

1. За допомогою функції CreateMesh (сітка розміром 40  40, діапазон зміни t від –5 до 5,  - від 0 до 2).

2. Задавши поверхню математично, для цього:

• Визначити функцію X(t)

Задати на осях змінних t і  по 41 крапці

i:=0..40 j:=0..40

для змінній ti із значеннями, що змінюються від -5 до 5 з кроком 0.25 ti := -5 + 0.25  i, а для змінній j _- від 0 до 2 з кроком /20 j := /20  j.

• Визначити матрицю Мi _j := X(ti,j) і відобразити її графічно.

За допомогою команди Формат контекстного меню викликати діалогове вікно “Формат 3-D графіка” і змінити:

• характеристики перегляду (Общєєвідвращеніє, Нахил)

• кольори і лінії поверхні (Зовнішній Відсвойства лінії, Властивості заливки)

• параметри осей (Осі)

• вид заголовка графіка (Назва).

• Вправа 10. Відобразити графічно перетин поверхонь і . Матриці для побудови поверхонь задати за допомогою функції CreateMesh, значення факультативних параметрів не указувати. Виконати однотонну заливку для поверхонь, вибравши з контекстного меню команду Формат. Також з контекстного меню вибрати ефекти Туман, Освітлення, Перспектива.

Контрольні питання

1. За допомогою якого оператора можна обчислити вираз?

2. Як вставити текстову область в документ Mathcad?

3. Чим відрізняється глобальне і локальне визначення змінних? За допомогою яких операторів визначаються?

4. Як змінити формат чисел для всього документа?

5. Як змінити формат чисел для окремого виразу?

6. Які системні (зумовлені) змінні Вам відомі? Як дізнатися їх значення? Як змінити їх значення?

7. Які види функцій в Mathcad Вам відомі?

8. Як вставити вбудовану функцію в документ Mathcad?

9. За допомогою яких операторів можна обчислити інтеграли, похідні суми і твори?

10. Як визначити дискретні змінні з довільним кроком? Який крок за умовчанням?

11. Як визначити індексовану змінну?

12. Які види масивів в Mathcad Вам відомі?

13. Яка системна змінна визначає нижню межу індексації елементів масиву?

14. Опишіть способи створення масивів в Mathcad.

15. Як проглянути вміст масиву, визначеного через дискретний аргумент?

16. Як побудувати графіки: поверхні; полярний; декартовий?

17. Як побудувати декілька графіків в одній системі координат?

18. Як змінити масштаб графіка?

19. Як визначити координату точки на графіці?

20. Як побудувати гістограму?

21. Які функції використовуються для побудови тривимірних графіків?

Лабораторна робота №2

ЧИСЕЛЬНІ МЕТОДИ ВИРІШЕННЯ СКАЛЯРНИХ РІВНЯНЬ

Мета роботи: сформувати:

• уявлення про застосування рівнянь в різних областях діяльності; знання про основні етапи вирішення рівняння;

• уміння застосовувати різні методи для уточнення кореня рівняння;

• навики у вибиранні того або іншого програмного засобу для перевірки правильності знайденого результату.

Теоретичні відомості

Найбільш загальний вид нелінійного рівняння:

,

(2.1)

де функція визначена і безперервна на кінцевому або нескінченному інтервалі .

Всяке число що обертає функцію у нуль називається коренем рівняння.

Вирішити рівняння (2.1) означає:

1. Встановити чи має рівняння коріння.

2. Визначити число коріння рівняння.

3. Знайти значення коріння рівняння із заданою точністю.

Відділення коріння

Відділення коріння – процедура знаходження відрізань, на яких рівняння (2.1) має тільки одне рішення.

В більшості випадків відділення коріння можна провести графічно. Для цього досить побудувати графік функції і визначити відрізки, на яких функція має тільки одну точку перетину з віссю абсцис.

У сумнівних випадках графічне відділення коріння необхідно підкріплювати обчисленнями. При цьому можна використовувати наступні положення:

• якщо безперервна функція приймає на кінцях відрізання значення різних знаків, те рівняння (2.1) має на цьому відрізку щонайменше один корінь;

• якщо функція до того ж і строго монотонна, то корінь на відрізку єдиний.

Розглянемо чисельні методи вирішення скалярних рівнянь на прикладах.

Метод дотичних

Завдання: Обчислити методом дотичних корінь рівняння

з точністю ?=0,001.

Алгоритм методу:

1. Задаємо функцію f(x):

2. Визначаємо функції першою і другою похідних цієї функції:

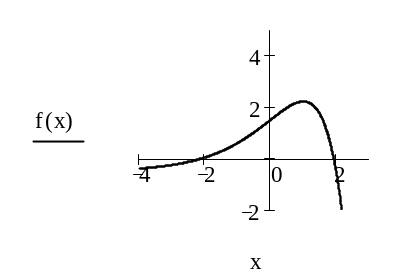
3. Відокремлюємо коріння рівняння графічно (рис 2.1):

Рис.2.1

Корінь належить відрізку [0,1].

Відрізок можна звузити, наприклад, узяти [0,0.5]

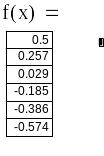
На відрізку існує корінь, оскільки значення функції на кінцях відрізання - різних знаків f(0)= 0,5; f(0,5)= -0,574.

Визначаємо нерухому крапку, порівнюючи знаки функції і другої похідної. У крапці х=0 знаки співпадають, значить, нерухомою крапкою буде значення х=0. Як х₀ візьмемо значення х=0,5.

4. Задаємо число кроків і початкове наближення:

Записуємо рекурентну формулу методу дотичних і роздруковуємо набутих значень:

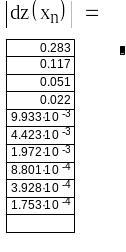
5. Визначимо критерій досягнення заданої точності при вирішенні рівняння методом дотичних і порівняємо його із значенням ε=0.001

Третє число в послідовності . Значить, число x₂=0,213 є вирішенням нашого рівняння.

Проаналізуємо отримані результати, побудувавши декілька графіків:

а)
б)
в)	Рис 2.2

На графіці (рис 2.2) показані залежності: а) значення кореня від кроку ітерації, б) набуття значення функції від кроку ітерації, в) отримання погрішності від кроку ітерації. З графіків видно, що рішення виходить на другому кроці ітераційного процесу.

Це підтверджується і набутих значень по формулах (аналітично).

6. Перевірка рішення задачі вбудованими можливостями пакету:

а) за допомогою функції root()

б) за допомогою блоку given ...find

в) за допомогою блоку given...minerr

7. Складемо функцію, що реалізовує метод дотичних:

Значить, коренем рівняння буде число x=0,213, яке виходить на 2 кроці. Графічні можливості пакету дозволили нам подивитися зсередини процес вирішення рівняння методом дотичних.

Метод хорд

Завдання: Вирішити рівняння методом хорд з точністю .

Алгоритм методу:

1. Відокремлюємо коріння. Цей етап рішення здійснюється за допомогою аналітичного або графічного методу. Після того, як корінь, що підлягає уточненню, відокремлений, за початкове наближення може бути вибрана будь-яка крапка [а,b].

Скористаємося графічним методом. Побудуємо графік функції і знайдемо точки перетину його з віссю Ох (рис.2.3).

Рис.2.3

Отримали два інтервали: [-3;-2], [1,5;2,5]. Інтервал, в якому уточнюватимемо корінь, - [1,5;2,5].

2. Уточнюємо коріння. Знаходимо першу похідну функції:

3. Визначаємо знаки f(x) на відрізку [1,5;2,5].

На даному відрізку функція міняє знак, означає на відрізку [1,5;2,5] дійсно існує корінь нашого рівняння.

4. Будуємо послідовність значень з використанням рекурентної формули методу хорд і проаналізуємо результати обчислених значень послідовності . Для цього розглянемо значення функції - ця величина є критерием досягнення заданої точності .

Починаючи з n=8, значення задовольняє критерію досягнення заданої точність , значить, х=1,927 є вирішенням заданого рівняння.

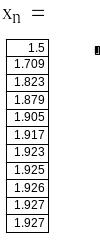
5. Створюємо функцію, що реалізовує обчислення кореня рівняння на відрізку [1,5;2,5] з точністю методом хорд. Рішенням буде число 1,927, що вийшло на восьмому кроці рішення.

6. Перевіряємо рішення

а)

б)

Відповідь: корінь рівняння по методу хорд рівний 1,927 з точністю 0.001, знайдений на восьмому кроці.

Хід роботи

1. Відокремити коріння рівняння, заданого по варіанту.

2. Уточнити один з них з точністю :

а) методом хорд;

б) методом дотичних;

3. Створити функції, що реалізовують вказані методи.

4. Побудувати графічну ілюстрацію методів.

5. Отримані результати перевірити за допомогою вбудованих функцій.

6. Оцінити точність набутих значень.

Завдання до лабораторної роботи №2

№	Рівняння	№	Рівняння

Контрольні питання

1. Що означає вирішити рівняння?

2. Які етапи вирішення рівняння з однією невідомою чисельними методами?

3. Які існують методи вирішення рівняння з однією невідомою?

4. У чому полягає етап відділення коріння при використанні чисельних методів вирішення рівняння?

5. Суть методу хорд. Графічна інтерпретація методу.

6. Суть методу дотичних. Графічна інтерпретація методу.

7. Яка умова є критерієм досягнення заданої точності при вирішенні рівняння методом хорд, дотичних?

8. Записати формулу знаходження значень послідовності при вирішенні рівняння методом хорд, дотичних.

Лабораторна робота №3

ЧИСЕЛЬНІ МЕТОДИ ВИРІШЕННЯ СИСТЕМ

ЛІНІЙНИХ РІВНЯНЬ

Мета роботи: сформувати уявлення про прямі і ітераційні методи вирішення систем лінійних рівнянь, виробивши вміння складати і застосовувати алгоритми і програми для вирішення систем рівнянь, дати навики у використанні програмних засобів для вирішення систем рівнянь.

Теоретичні відомості

Розглянемо систему, що складається з лінійних рівнянь алгебри з невідомими:

(3.1)

яка може бути записана в матричному вигляді:

,

(3.2)

де - прямокутна матриця розмірності :

- вектор порядку :

- вектор порядку :

Вирішенням системи (3.1) називається така впорядкована сукупність чисел яка обертає всі рівняння системи (3.1) у вірну рівність.

Прямими методами вирішення систем лінійних рівнянь називаються методи, що дають вирішення системи за кінцеве число арифметичних операцій.

Ітераційними методами вирішення систем лінійних рівнянь називаються методи, що дають вирішення системи рівнянь як межу послідовності наближень, що обчислюються по одноманітній схемі.

Розглянемо чисельні методи вирішення систем лінійних рівнянь на прикладі методів Гауса-Жордана, простій ітерації, Зейделя.

Метод Гауса-Жордана

Завдання: вирішити систему методом Гауса-Жордана з точністю :

Алгоритм рішення

1. Вводимо матрицю коефіцієнтів при невідомих А і матрицю вільних членів В.

2. Задаємо функцію, що реалізовує метод Гауса-Жордана

3. Перевіряємо рішення за допомогою вбудованих функцій Mathсad.

а)

б)

в)

Ответ:

Метод Зейделя

Завдання: вирішити систему методом Зейделя з точністю :

Алгоритм рішення

1. Вводимо матрицю коефіцієнтів при невідомих і матрицю вільних членів.

2. Транспонуємо матрицю А (транспонована матриця – це матриця, стовпці якої є рядками початкової матриці).

3. Умножаємо ліву і праву частини початкової системи на матрицю .

4. Отримуємо систему вигляду . Для цього розділимо коефіцієнти кожного рядка матриці М на відповідний вирішуючий елемент рядка. Отримаємо приведену систему, до якої застосуємо метод Зейделя.

5. Складемо функцію, що реалізовує метод Зейделя

Відповідь: вирішенням системи трьох лінійних рівнянь є вектор знайдений на 19-му кроці ітерації.

Метод простій ітерації

Завдання: вирішити систему методом простій ітерації з точністю :

Алгоритм методу

1. Приводимо початкову систему до вигляду з переважаючими діагональними коефіцієнтами. Для цього перше рівняння запишемо третім, третє рівняння помножимо на 2, віднімемо друге і запишемо на першому місці, а друге рівняння помножимо на 2, віднімемо перше і запишемо на другому місці.

Коефіцієнти, розташовані по діагоналі і підкреслені, є переважаючими по рядку.

2. Складаємо матриці коефіцієнтів при невідомих в лівій частині і вільних членів.

3. Отримуємо перетворену систему.

Розділимо для цього кожне рівняння на свій діагональний коефіцієнт і виразимо з кожного рівняння діагональне невідоме.

4. Перевіряємо одну з розумів збіжності ітераційного процесу.

Встановлюватимемо збіжність, тобто «зануримо» систему в простір з однією з трьох метрик: ρ₁ , ρ₂ , ρ₃ .

Визначимо коефіцієнти стиснення а) за допомогою вбудованих функцій MathCad; б) за допомогою формул.

Відмітимо, що всі коефіцієнти менше одиниці, означає систему можна занурити в простір з будь-якою з метрик.

Зупинимося на просторі з метрикою ρ_2.

Побачимо, що ітераційний процес сходиться, причому

а)

б)

5. Знаходимо критерій досягнення заданої точності при вирішенні системи рівнянь методом простій ітерації. Для досягнення точності ε=0.001 наближення потрібно знаходити до тих пір, поки буде виконаються нерівність .

6. Обчислюємо значення ітераційної послідовності.

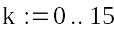
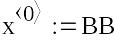
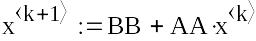
7. Для визначення, яке наближення буде рішенням, необхідно знайти відстані між двома сусідніми наближеннями по метриці ρ₂.

Набутого десятого значення суми модулів різниць коефіцієнтів при невідомих, рівне задовольняє умові критерію. Це означає, що в таблиці значень х дев'ятий стовпець є вирішенням системи рівнянь методом простій ітерації.

8. Візуалізуємо набутих значень.

Рис 3.1

Графіки показують, що, починаючи з k=10, всі три лінії перестають заломлюватися, а значить, десяте наближення буде рішенням наший системи рівнянь методом простій ітерації.

Відповідь: вирішенням системи трьох лінійних рівнянь є вектор , знайдений на 10-му кроці ітерації.

Хід роботи

1. Вирішити систему рівнянь з трьома невідомими:

• методом Гауса-Жордана

• методом простій ітерації

• методом Зейделя

з точністю  = 0,001.

2. Скласти функції, що реалізовують методи.

3. Перевірити вирішення за допомогою вбудованих функцій пакету MATHCAD.

Завдання до лабораторної роботи №3

№	Завдання	№	Завдання

Контрольні питання

1. Які ви знаєте групи методів вирішення систем лінійних рівнянь з п невідомими?

2. Які методи відносяться до прямих методів вирішення систем лінійних рівнянь з п невідомими?

3. Які методи відносяться до наближених методів вирішення систем лінійних рівнянь з п невідомими?

4. Що означає вирішити систему рівнянь з п невідомими?

5. У чому полягає суть методу Гаусса—жордана для вирішення систем рівнянь?

6. Як формулюється правило прямокутника для вирішення систем методом Гаусса—жордана?

7. Що таке метрика?

1. Що таке стискаюче відображення?

2. У чому полягає суть методу простій ітерації для вирішення систем рівнянь?

10. Яку систему можна вирішувати методом простій ітерації?

11. Як привести систему до вигляду з переважаючими діагональними коефіцієнтами?

12. Як знаходиться відстань між двома наближеннями в просторі з метрикою ρ₁ , ρ₂ , ρ₃?

13. Які достатні умови збіжності ітераційного процесу при вирішенні систем?

14. Як знайти коефіцієнт стиснення?

15. Яка умова є критерієм досягнення заданої точності при вирішенні систем лінійних рівнянь методом простій ітерації, методом Зейделя?

16. Як будується ітераційна послідовність значень при вирішенні систем рівнянь методом простій ітерації, методом Зейделя?

Лабораторна робота №4

НАБЛИЖЕННЯ ЗНАЧЕННЯ ТАБЛИЧНО ЗАДАНОЇ ФУНКЦІЇ В ТОЧЦІ ЗА ДОПОМОГОЮ ІНТЕРПОЛЯЦІЙНИХ ПОЛІНОМІВ

Мета роботи: сформувати у студентів уявлення про застосування інтерполяції функцій для вирішення завдань, прищепити уміння складати і застосовувати інтерполяційні формули Лагранжа заданому ступеню, многочлени Ньютона, сплайни і оцінювати їх погрішності, дати навики у використанні програмних засобів для перевірки отриманих результатів.

Теоретичні відомості

Інтерполяційний поліном Лагранжа

Хай задана функція

X	0,41	1,55	2,67	3,84
Y	2,63	3,75	4,87	5,03

Побудувати інтерполяційний многочлен Лагранжа для функції заданої табличний, знайти значення цієї функції в точці х=1, 91, побудувати графіки отриманого многочлена Лагранжа функції, заданій табличний, і многочлена n-ой ступеня і оцінити точність наближення.

1. Вводимо матриці початкових даних:

Знаходимо величину n – показник ступеня многочлена:

Задаємо змінні:

Записуємо формулу многочлена Лагранжа в символьному вигляді:

Перевіряємо правильність записаної формули:

Знаходимо значення функції в шуканій точці х=1, 91:

2. Знаходимо коефіцієнти інтерполяційного многочлена.

Знаходимо матрицю певного вигляду:

Обчислюємо коефіцієнти полінома:

Отримали многочлен третього ступеня:

3. Правильність знайдених коефіцієнтів перевіримо, підставивши значення х з числа заданих, і знайдемо значення функції при х=1,91.

Значення функції повністю співпадає із значенням, знайденим вище.

4. Будуємо графіки значень vxi і отриманих многочленів f(x), P(x

Рис.4.1

З рис. 4.1 видно, що графіки побудованого многочлена Лагранжа f(x) і функції P(x) проходять через вузли інтерполяції.

5. Перевіряємо набутого значення за допомогою вбудованої функції:

6. Складаємо функцію, що реалізовує інтерполяцію функцій многочленом Лагранжа:

Інтерполяція сплайнами

Інтерпольована функція складається з шести вузлів (n=5)

x	0,41	0,46	0,52	0,60	0,65	0,72
F(x)	2,57	2,325	2,09	1,86	1,75	1,62

Знайти значення коефіцієнтів що визначають кубічний сплайн на п'яти часткових відрізках.

Складемо систему що складається з 15 рівнянь

Набудемо значень коефіцієнтів які визначають шуканий сплайн.

Переконаємося, що знайдений сплайн задовольняє заданим властивостям

Збіг значень, знайдених за допомогою побудованого сплайна і вбудованої функції інтерполяції, можна перевірити і за допомогою функції сплайн-интерполяции

Побудуємо графіки сплайн-функции, функції r(x), і заданих значень у (рис.4.2).

Рис.4.2

Інтерполяційний поліном Ньютона

Вкажемо форму запису інтерполяційного полінома Рп(х)_, яка допускає уточнення результатів інтерполяції послідовним збільшенням нових вузлів. При цьому використовуватимемо розділені різниці функції, що є зручним апаратом при роботі з табличний заданими функціями.

Хай для функції f(x) задані вузли інтерполяції х0, х1...хn:

y0 = f(x0), y1 = f(x1)... yn = f(xn) - відповідні значення функції.

Розділеними різницями першого порядку називаються величини, що мають сенс середніх швидкостей зміни функції і обчислювані по формулах:

(4.1)

(4.2)

Аналогічно визначаються розділені різниці другого порядку:

(4.3)

і так далі

У загальному випадку розділені різниці к-го порядку визначаються через розділені різниці (к-1) -го порядку по рекурентній формулі:

(4.4)

Обчислення розділених різниць зручно проводити в таблиці

		Розділені різниці
		1-го порядку	2-го порядку	3-го порядку	4-го порядку
x0	f(x0)
x1	f(x1)	f(x0,x1)
x2	f(x2)	f(x1,x2)	f(x0,x1,x2)
x3	f(x3)	f(x2,x3)	f(x1,x2,x3)	f(x0,x1,x2,x3)
x4	f(x4)	f(x3,x4)	f(x2,x3,x4)	f(x1,x2,x3,x4)	f(x0,x1,x2,x3,x4)

Інтерполяційний поліном може бути записаний через розділені різниці у вигляді

(4.5)

Записаний поліном носить назва інтерполяційного полінома Ньютона

Хід роботи

1. Побудувати за наявними даними інтерполяційний многочлен Лагранжа;

2. Побудувати інтерполяційний поліном Ньютона;

3. Виконати інтерполяцію сплайнами;

4. Знайти значення функції в точці x, використовуючи інтерполяційний многочлен Лагранжа, поліном Ньютона, сплайни, побудувати графічну ілюстрацію інтерполяції.

Завдання до лабораторної роботи №4

1.				2.		3.
x	y			x	y	х	y
0,43	1,63597			0,43	1,63597	0,43	1,63597
0,48	1,73234			0,48	1,73234	0,48	1,73234
0,55	1,87686			0,55	1,87686	0,55	1,87686
0,62	2,03045			0,62	2,03045	0,62	2,03045
0,70	2,22846			0,70	2,22846	0,70	2,22846
0,75	2,35973			0,75	2,35973	0,75	2,35973
у точці x = 0,702				у точці x = 0,702		у точці x = 0,702
4.				5.		6.
x			y	х	y	х	y
0,43			1,63597	0,02	1,02316	0,35	2,73951
0,48			1,73234	0,08	1,09590	0,41	2,30080
0,55			1,87686	0,12	1,14725	0,47	1,96864
0,62			2,03045	0,17	1,21483	0,51	1,78776
0,70			2,22846	0,23	1,30120	0,56	1,59502
0,75			2,35973	0,30	1,40976	0,64	1,34310
у точці x = 0,608				у точці x = 0,203		у точці x = 0,482
7.				8.		9.
x		y		х	y	х	y
0,02		1,02316		0,35	2,73951	0,41	2,57418
0,08		1,09590		0,41	2,30080	0,46	2,32513
0,12		1,14725		0,47	1,96864	0,52	2,09336
0,17		1,21483		0,51	1,78776	0,60	1,86203
0,23		1,30120		0,56	1,59502	0,65	1,74926
0,30		1,40976		0,64	1,34310	0,72	1,62098
у точці x = 0,102				у точці x = 0,436		у точці x = 0,616

10.		11.		12.
x	y	х	y	х	y
0,02	1,02316	0,35	2,73951	0,41	2,57418
0,08	1,09590	0,41	2,30080	0,46	2,32513
0,12	1,14725	0,47	1,96864	0,52	2,09336
0,17	1,21483	0,51	1,78776	0,60	1,86203
0,23	1,30120	0,56	1,59502	0,65	1,74926
0,30	1,40976	0,64	1,34310	0,72	1,62098
у точці x = 0,114		у точці x = 0,552		у точці x = 0,487

13.			14.			15.
x	y		х		y	x	y
0,02	1,02316		0,35		2,73951	0,41	2,57418
0,08	1,09590		0,41		2,30080	0,46	2,32513
0,12	1,14725		0,47		1,96864	0,52	2,09336
0,17	1,21483		0,51		1,78776	0,60	1,86203
0,23	1,30120		0,56		1,59502	0,65	1,74926
0,30	1,40976		0,64		1,34310	0,72	1,62098
у точці x = 0,285			у точці x = 0,526			у точці x = 0,665
16.		17.				18.
х	y	х		y		х		y
0,41	2,57418	0,68		0,80866		0,11		9,05421
0,46	2,32513	0,73		0,89492		0,15		6,61659
0,52	2,09336	0,80		1,02964		0,21		4,69170
0,60	1,86203	0,88		1,20966		0,29		3,351069
0,65	1,74926	0,93		1,34087		0,35		2,73951
0,72	1,62098	0,99		1,52368		0,40		2,36522
у точці x = 0,537		у точці x = 0,774				у точці x = 0,275

19.		20.		21.
x	y	х	y.	х	y
0,68	0,80866	0,11	9,05421	0,05	0,050042
0,73	0,89492	0,15	6,61659	0,10	0,100335
0,80	1,02964	0,21	4,69170	0,17	0,171657
0,88	1,20966	0,29	3,351069	0,25	0,255342
0,93	1,34087	0,35	2,73951	0,30	0,309336
0,99	1,52368	0,40	2,36522	0,36	0,376403
у точці x = 0,896		у точці x = 0,314		у точці x = 0,263

22.		23.					24.
x	y	Х		y			x		y
0,68	0,80866	0,11		9,05421			0,68		0,80866
0,73	0,89492	0,15		6,61659			0,73		0,89492
0,80	1,02964	0,21		4,69170			0,80		1,02964
0,88	1,20966	0,29		3,351069			0,88		1,20966
0,93	1,34087	0,35		2,73951			0,93		1,34087
0,99	1,52368	0,40		2,36522			0,99		1,52368
у точці x = 0,715		у точці x = 0,235					у точці x = 0, 955

25.		26.			27.
x	y	x		y	x		y
0,11	9,05421	0,51		9,05421	0,115		5,05421
0,15	6,61659	0,55		6,61659	0,159		4,61659
0,21	4,69170	0,61		4,69170	0,218		3,69170
0,29	3,351069	0,69		3,35106	0,294		2,35106
0,35	2,73951	0,75		2,73951	0,353		1,73951
0,40	2,36522	0,80		2,36522	0,408		0,36522
у точці x = 0,332		у точці x = 0,7491			у точці x = 0,256
28.		29.			30.
х	y	х	y		х	y
0,41	2,57418	0,68	0,80866		0,11	9,05421
0,46	2,32513	0,73	0,89492		0,15	6,61659
0,52	2,09336	0,80	1,02964		0,21	4,69170
0,60	1,86203	0,88	1,20966		0,29	3,351069
0,65	1,74926	0,93	1,34087		0,35	2,73951
0,72	1,62098	0,99	1,52368		0,40	2,36522
у точці x = 0,437		у точці x = 0,9475			у точці x = 0,3535

Контрольні питання

1. Що таке інтерполяція?

2. Що таке параболічна інтерполяція?

3. Що таке вузли інтерполяції?

4. У чому полягає завдання відшукання інтерполюючого многочлена?

5. Як побудувати інтерполяційний многочлен Лагранжа?

6. Як визначається погрішність методу інтерполяції за допомогою формули Лагранжа?

7. Яка схема Ейткена?

8. Як утворюються розділені різниці?

9. Як зв'язані розділені різниці і похідна?

10. Що таке зворотна інтерполяція?

11. Що таке сплайн? Як відбувається процес інтерполяції сплайнами?

12. Що таке кінцева різниця першого порядку? Як вона знаходиться?

13. Що таке кінцева різниця другого порядку? Як вона знаходиться?

14. Що таке кінцева різниця N- го порядку? Як вона знаходиться?

15. Перша інтерполяційна формула Ньютона для рівновіддалених вузлів.

16. Друга інтерполяційна формула Ньютона для рівновіддалених вузлів.

Лабораторна робота №5

ЧИСЕЛЬНЕ ДИФЕРЕНЦІЮВАННЯ

Мета роботи: навчитися використовувати формули інтерполяції (многочлени Лагранжа і Ньютона) для знаходження першої і другої похідних функції, заданої табличний.

Теоретичні відомості

Диференціювання функцій за допомогою інтерполяційної формули Лагранжа

Для функції, заданої табличний, побудуємо інтерполяційний многочлен ступінь якого не вищий і виконані умови:

(5.1)

Шукатимемо у вигляді:

(5.2)

де - многочлен ступеня причому

(5.3)

Очевидно, що вимога (5.3) з обліком (5.2) забезпечує виконання умов (5.1).

Многочлени складемо таким чином:

(5.4)

де - постійний коефіцієнт, значення якого знаходиться з першої частини умови (5.3):

(5.5)

Підставивши у (5.5) і далі в (5.3), остаточно отримаємо:

(5.6)

Формула (5.6) остаточно вирішує поставлену задачу.

Хай необхідно знайти першу і другу похідні функції заданою табличний на інтервалі [2,3], використовуючи формулу Лагранжа. Алгоритм методу наступний:

1. Будуємо таблицю значень на заданому відрізку:

2. Записуємо інтерполяційну формулу Лагранжа при диференціюванні функції з рівновіддаленими вузлами:

3. Знаходимо значення похідної для заданих значень :

4. Набутих значень перевіримо, використовуючи функцію знаходження першої похідної:

5. Графічно зобразимо отримані значення першої похідної і значення, отримані по інтерполяційній формулі Лагранжа (рис 5.1):

Рис 5.1

Хід роботи

5. Обчислити значення першої похідної функції, заданої табличний, використовуючи інтерполяційні многочлени Лагранжа і оцінити погрішність методу;

6. Скласти функцію, що дозволяє знаходити значення першої похідної в даних крапках і будь-якій проміжній крапці;

7. Візуалізувати отримані результати.

Завдання до лабораторної роботи №5

№	F(x)	[a;b]	№	F(x)	[a;b]
		[1;2]	15.		[0;1]
		[2;3]	16.		[2;3]
		[5;6]	17.		[2;3]
		[-1;0]	18.		[-1;0]
		[2;3]	19.		[2;3]
		[2;3]	20.		[-2;-1]
		[5;6]	21.		[-2;-1]
8.		[0,1;1,1]	22.		[2;3]
9.		[0;1]	23.		[0,5;1,5]
10.		[0,1;1,1]	24.		[0;1]
11.		[0,5;1,5]	25.		[1,1;2,1]
12.		[0;1]	26.		[0;1]
13.		[0,5;1,5]	27.		[0;1]
14.		[1,1;2,1]	28.		[1,1;2,1]

Контрольні питання

1. У яких випадках використовують чисельне диференціювання?

2. У чому особливість завдання чисельного диференціювання?

3. Графічна інтерпретація чисельного диференціювання.

4. Інтерполяційна формула Лагранжа для рівновіддалених вузлів.

5. Формула чисельного диференціювання на основі інтерполяційної формули Лагранжа.

6. Формула для оцінки погрішності чисельного диференціювання по формулі Лагранжа.

7. Формула чисельного диференціювання на основі інтерполяційних формул Ньютона.

8. Формула для оцінки погрішності чисельного диференціювання по формулах Ньютона.

9. Як впливає на точність чисельного диференціювання величина кроку?

Лабораторна робота №6

ЧИСЕЛЬНЕ ІНТЕГРУВАННЯ

Мета роботи: ознайомитися з чисельними методами обчислення певних інтегралів, навчитися вирішувати завдання з використанням формули Сімпсона, трапецій, правих і лівих прямокутників, методу Монте-Карло і оцінювати погрішність всіх перерахованих формул.

Теоретичні відомості

З геометричної точки зору певний інтеграл

(6.1)

Є площа фігури, обмежена графіком функції і прямими (рис. 6.1).

Рис.6.1

Розділимо відрізок на N рівних відрізків завдовжки де

(6.2)

Тоді координата правого кінця i-го відрізання визначається по формулі:

(6.3)

де

Проста оцінка площі під кривій може бути отримана як сума площ прямокутників, одна із сторін якого співпадає з відрізком а висота рівна значенню функції в крапці (метод лівих прямокутників) або в крапці (метод правих прямокутників).

Значення певного інтеграла обчислюється по формулах:

	(6.4)
	(6.5)

Для методів лівих і правих прямокутників відповідно.

Можна підвищити точність обчислення певного інтеграла якщо замінити реальну функцію на кожному з інтегралів відрізком прямої, що проходить через крапки з координатами . В цьому випадку фігура, обмежена графіком функції і прямими є трапецією. Шуканий певний інтеграл визначається як сума площ всіх трапецій (метод трапецій):

(6.6)

Вища точність обчислення інтегралів забезпечується при використанні параболічної інтерполяції по трьом сусіднім крапкам. Шуканий певний інтеграл визначається як сума площ всіх параболічних сегментів (формула Сімпсона):

(6.7)

У формулі Симпсона N повинне бути парним числом.

Розглянемо рішення задачі про обчислення певного інтеграла в пакеті Mathcad.

Метод прямокутників

Обчислити наближене значення інтеграла використовуючи формули лівих і правих прямокутників, при

1. Задаємо функцію відрізок [а,b] і функцію знаходження диференціалів n-го порядку.

2. Знаходимо значення інтеграла заданої функції для використання його в подальшому рішенні для порівняння:

Складемо функцію, вхідними параметрами якої є: – ліва і права межі інтервалу; – кількість розбиття; – якщо має значення “left”, то йде підрахунок по формулі лівих прямокутників, будь-яке інше – по формулі правих прямокутників.

Результати обчислень по формулах правих і лівих прямокутників:

Погрішність показує, що набутого значення інтеграла вірне.

Метод Сімпсона

Обчислити наближене значення інтеграла використовуючи загальну формулу Сімпсона, при

Складемо функцію, вхідними параметрами якої є: – ліва і права межі інтервалу; – кількість розбиття. Індекси E і U позначають парність і непарність відповідно.

Метод трапецій

Обчислити наближене значення інтеграла використовуючи формулу трапецій, при

Функція, що реалізовує обчислення інтеграла методом трапецій:

Метод Монте-Карло

Обчислити наближене значення інтеграла використовуючи метод Монте-Карло, при

Реалізація методу Монте-Карло:

Порівнюючи точне і чисельне значення інтегралів, знаходимо абсолютну погрішність.

Хід роботи

1. Знайти наближене значення інтеграла заданої функції f(x) на відрізку [а, b] по формулах:

- трапецій

- Сімпсона

- прямокутників

-Монте-Карло при діленні відрізання на 1000 рівних частин.

2. Провести оцінку погрішності методів інтеграції.

3. Порівняти точність отриманих результатів.

Завдання до лабораторної роботи №6

№	Функція	Інтервал
		[0;3]
		[0;1]
		[1;2]
		[2;3]
		[0;0.5]
		[1,2;2,2]
		[0,5;1,5]
		[2;3]
		[1;2]
		[-0,5;0,5]
		[0,1;1,1]
		[-2;0]
		[0;1]
		[3;5]
		[2;3]
		[-1;0]
		[0;3]
		[0;5]
		[-3;-1]
		[0;1]
		[4;5]
		[0;3]
		[0,1;1,1]
		[1;2]
		[1,5;2,5]
		[1,7]
		[p;p/2]
		[0;1]

Контрольні питання

1. У якому випадку використовується чисельна інтеграція?

2. Постановка завдання чисельної інтеграції.

3. Які існують методи інтеграції функції?

4. Графічна інтерпретація методу трапецій.

5. Як оцінити погрішність методу трапецій?

6. Графічна інтерпретація методу Сімпсона.

7. Як оцінити погрішність методу Сімпсона?

8. Графічна інтерпретація методу прямокутників.

9. Як оцінити погрішність методу прямокутників?

10. Чим відрізняються формули методу трапецій і методу Сімпсона?

11. Як впливає на точність чисельної інтеграції величина кроку h?

12. Чим відрізняється обчислення погрішності методу трапецій і Сімпсона?

СПИСОК РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ

1. Бахвалов Н.С, Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Лаборатория Базовых Знаний, 2001.

2. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, I960.

3. Заварыкин В. М., Житомирский В. Г., Лапчик М. П. Техника вычислений и алгоритмизация. – М.: Просвещение, 1987.

4. Лапчик М.П. Вычисления. Алгоритмизация. Программирование. – М.: Просвещение, 1988.

5. Пулькин С. П. Теория и практика вычислений. – М.: Наука, 1967.

6. Вержбицкий В.М. Численные методы: Учеб. пособие для вузов.–М.:Высшая школа, 2001.

7. Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad.– СПб.: БХВ-Петербург, 2005.

Додаток 1