Тюрникова Г.В. Курс высшей математики для начинающих. Гл.8/14. Обыкновенные дифференциальные уравнения.

Глава 8. Обыкновенные дифференциальные уравнения.

При изучении интегрального исчисления функций одной переменной приходилось отыскивать неизвестную функцию по ее производной или дифференциалу. Практически решалось уравнение или (у – неизвестная функция от х, f(x) – заданная функция), которое является простейшим дифференциальным уравнением.

Гораздо чаще приходится иметь дело с уравнениями более сложного вида. В эти уравнения может входить не только у^’, независимая переменная х, но и сама неизвестная функция.

Пример:

Заменяя на , эти уравнения можно переписать в дифференциальной форме:

, , .

Мы будем рассматривать такие дифференциальные уравнения, в которых неизвестная функция зависит только от одного аргумента. Такие уравнения называют обыкновенными. Дифференциальные уравнения, в которых неизвестная функция зависит от многих/нескольких аргументов, называют уравнениями в частных производных^*). В настоящем курсе будем рассматривать обыкновенные дифференциальные уравнения.

Раздел 8.1. Дифференциальные уравнения первого порядка.

8.1.1. Задачи, приводящие к дифференциальным уравнениям.

З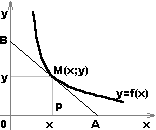 адача 1. Найти кривую, обладающую тем свойством, что отрезок любой ее касательной, заключенной между осями координат, делится пополам в точке касания.

Решение.

Пусть - уравнение искомой кривой, М(х,у) – произвольная точка, лежащая на этой кривой.

Угловой коэффициент касательной в этой точке равен у^’ . По условию задачи АМ=МВ, т.е. ОР=РА=х, а, значит, в любой точке М, принадлежащей кривой , следовательно, .

Получилось соотношение, связывающее неизвестную функцию у, независимую переменную х, производную от у по х, т.е. получилось дифференциальное уравнение относительно у. Этому уравнению удовлетворяет функция ^*), где С – любое число.

Итак, указанным в задаче свойством обладает бесконечное множество/ «семейство» кривых, отличающихся между собой значением постоянной С. Это семейство равносторонних гипербол, асимптотами которых являются оси координат.

Для того, чтобы из этого семейства выделить одну кривую, достаточно задать конкретную точку (х₀,у₀), через которую будет проходить кривая, и определить соответствующее значение С из .

Задача 2.(радиоактивный распад). Экспериментальным путем установлено, что скорость радиоактивного распада пропорциональна количеству нераспавшегося вещества. Считая, что начальное количество вещества равно М₀, найти зависимость между количеством нераспавшегося вещества М и временем t.

Решение.

Скорость радиоактивного распада равна производной от количества вещества М по времени t, т.е. . Но по условию

,

где k – коэффициент пропорциональности. Знак минус берется потому, что с возрастанием t количество вещества М уменьшается. Обращаем внимание на тот факт, что величина М₀ не входит в полученное дифференциальное уравнение: она войдет как начальное условие .

Уравнению удовлетворяет функция . Подставляя начальные условия , получается С=М₀.

Следовательно, частное решение, удовлетворяющее условиям задачи

.

Постоянную k можно установить экспериментально (такой метод очень часто применяется в подобных случаях), установив количество нераспавшегося вещества в какой-то момент времени.

Задача 3. (охлаждение тела). Согласно закону, установленному Ньютоном, скорость охлаждения тела пропорциональна разности между температурой тела и температурой окружающей среды^*). Требуется получить закон (аналитический вид) охлаждения тела.

Решение.

Пусть тело нагрето до температуры Т₀. Температуру окружающей среды будем считать постоянной и равной Т_с (Т_с<Т₀).

Найдем зависимость между изменяющейся температурой Т тела и временем t.

Пусть в момент времени t температура тела равна Т. Скорость изменения температуры , т.е. , по закону Ньютона пропорциональна разности Т-Т_с. Следовательно,

.

Знак минус выбран потому, что с возрастанием t температура Т тела уменьшается. Коэффициент пропорциональности k зависит как от физических свойств тела, так и от его геометрической формы (понятно, что скорость охлаждения раскатанного листа стали больше, чем стального слитка).

Разделяя переменные, получим

.

Отсюда

,

или, что все равно

.

Подставляя начальное условие , получается С=Т₀-Т_с.

Тогда закон охлаждения тела имеет вид

.

Коэффициент пропорциональности k должен быть либо задан, либо установлен экспериментальным путем измерения температуры Т в некоторый момент времени t. Заметим, что теоретически температура тела сравняется с температурой окружающей среды лишь при .