Invk (x1, … , xn),
который будем называть индуктивным утверждением. Назначение этого предиката состоит в том, чтобы описать соотношение между переменными в этой точке. Всякий раз, когда исполнение программы достигает точки k, предикат invk (x1, … , xn) должен быть истинным для текущих значений x1, … , xn в этой точке.
Индуктивное утверждение, приписанное циклу, принято называть инвариантом цикла. Инвариант цикла может приписываться точке входа в цикл или любой другой точке цикла, которая лежит на каждой трассе через цикл.
Будем считать, что программа аннотируется выбором контрольных точек (на входе программы, выходе программы и на каждом пути через цикл), с каждой из которых связывается индуктивное утверждение (инвариант):
Invt1 (x1, … , xn): p ; invt2 (x1, … , xn): q ; invt3 (x1, … , xn) ; … ,
где t1 – точка входа (после оператора START), t2 – точка выхода (перед оператором STOP), t3 – контрольная точка инварианта цикла.
Шаг 3. Определение набора условий корректности для всех путей между соседними контрольными точками программы
Пусть путь ведет от контрольной точки r к контрольной точке t (случай r = t не исключается) и не содержит никаких других контрольных точек и пусть этот путь проходит через последовательность операторов A1, A2, … , Ai,, … , Ak, где Ai – оператор присваивания или условие , где { +, - }.
Определим условие U пути между двумя соседними контрольными точками графа потока управления программы следующим образом:
U: invr(x1, … , xn) u0
(из истинности предиката в начальной контрольной точке r следует истинность условия U0), где последовательность U0, U1, … , Uk задается по индукции (методом обратной подстановки):
Uk: invt (x1, … , xn) – условие определяется предикатом в контрольной точке t;
Пусть Ui определено. Тогда возможны два случая:
Ai – оператор присваивания xs := f (x1, … , xn), тогда
Ui-1: Ui ( xs f (x1, … , xn));
Ai – условный оператор , тогда
Ui-1: Ui при = + или
Ui-1: Ui при = –
Пример
Пусть соответствует последовательности:
x = f1 (x); g+ (x); x = f2 (x); h– (x); x = f3 (x);
Тогда
P : invr (x) – входной предикат;
U5 : Q = invt (x);
U4 : Q ( f3 (x) );
U3 : ( h (x) Q ( f3 (x) ) );
U2 : ( h ( f2 (x) ) Q ( f3 ( f2 (x) ) ) );
U1: ( g (x) ( h ( f2 (x) ) Q ( f3 ( f2 (x) ) ) );
U0: ( g (f1 (x) ) ( h ( f2 (f1 (x) ) ) Q ( f3 ( f2 (f1 (x) ) ) );
Окончательно условие пути имеет вид:
U: P ( g (f1 (x) ) ( h ( f2 (f1 (x) ) ) Q ( f3 ( f2 (f1 (x) ) ) );
Шаг 4. Доказательство истинности составленных условий корректности
Введенное понятие условия U между соседними контрольными точками позволяет свести задачу анализа частичной корректности программы Prgm к доказательству истинности условий между любыми соседними контрольными точками программы Prgm.
Теорема (без док-ва). Программа Prgm частично корректна относительно предусловия P и постусловия Q, если для каждого пути между соседними контрольными точками условие пути U истинно.
Важность этой теоремы состоит в том, что она позволяет абстрагироваться от конкретных процессов между соседними контрольными точками вычислений по программе и рассматривать только условия U между соседними контрольными точками, т.е. рассматривать только характеристики статической структуры программы.
Возможности доказательства условий корректности U зависят от проблемной области.
Пример
Доказать частичную корректность программы вычисления частного и остатка от деления целых чисел x и y.
Программа на Паскале:
r := x; q := 0;
while y r do
begin r := r – y; q := q + 1 end
Блок-схема этой программы имеет вид:
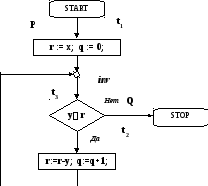
Разрезание цикла программы.
Разрежем цикл программы в точке входа в цикл (точка t3)..
Получение аннотированной программы.
Запишем индуктивные утверждения для программы в контрольных точках t1, t и t3.
P: invt1( x, y ) ( x 0 ) ( y > 0 ); – условие корректных исходных данных
Q: invt2 ( x, y, q, r ) ( x = r + y*q ) ( r < y ); – условие выхода из цикла
invt3 ( x, y, q, r ) : x = r + y*q – инвариант цикла.
Определение набора условий корректности для всех путей между соседними контрольными точками программы.
Путями между контрольными точками являются:
1 : от входа программы к началу цикла (t1 – t3);
2 : от начала цикла через тело цикла обратно к началу цикла (t3 – t3);
3 : от начала цикла через условие цикла к выходу программы (t3 – t2).
Тогда
U1 : P invt3 ( r x, q 0 )
( x 0 ) ( y > 0 ) x = x + y*0
( x 0 ) ( y > 0 ) x = x
( x 0 ) ( y > 0 ) true
U2 : invt3 ( x, y, q, r )
( ( y r ) invt3 ( x, y, q q+1, r r – y) )
(x = r + y*q ) ( ( y r ) ( x = ( r - y ) + y*(q + 1))) (x = r + y*q ) ( ( y r ) (x = r + y*q ) );
U3 : invt3 ( x, y, q, r ) ( ( y > r ) Q )
(x = r + y * q ) ( ( y > r ) (x = r + y * q ) ( r < y ) )
4. Доказательство истинности условий U.
Условие U1 – истина, так как x1 x2 – тождественная истина, если x2 – истина.
Преобразуем условие U2.
(x = r + y * q ) ( ( y r ) (x = r + y * q ) )
( (x = r + y * q ) ( y r ) ) (x = r + y * q ) )
( (x = r + y * q ) ( y r ) ) ( x = r + y * q )
( x = r + y * q ) ( y r ) ( x = r + y * q )
( y r ) true ( y r ) true.
Следовательно, U2 – истина (по аналогии с U1).
Преобразуем условие U3.
(x = r + y * q ) ( ( y > r ) (x = r + y * q ) ( r < y ) )
(x = r + y * q ) ( y > r ) (x = r + y * q ) ( r < y )
( y > r ) ( r < y ), так как x = r + y * q – true.
Следовательно, U3 – истина
Таким образом, доказана истинность всех трех условий корректности и. следовательно, установлено свойство частичной корректности программы.
Пример 2
Доказать
частичную корректность программы
вычисленияz
= [x]
для
любого целого x
0.
[x]
есть
наибольшее целое число k
такое, что k
x.
Решение
Метод вычисления, на котором основана программа, основывается на известном соотношении: 1 + 3 + 5 + … + (2k + 1) = (k + 1)2 для каждого k 0.
Пусть значение суммы запоминается в s, а нечетные числа 2k + 1 – в n.
Программа на Паскале:
k := 0; s:= 0; n:= 1;
s := s + n;
while x s do
begin k := k +1; n := n + 2;
s := s + n;
end;
z := k;
Блок-схема этой программы имеет вид:
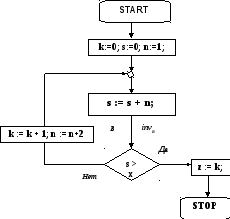
Разрежем цикл программы в точке B.
Получение аннотированной программы.
Запишем индуктивные утверждения для программы в контрольных точках A, B и C.
P: invA(x) x0 ; – условие корректных входных данных
Q: invС ( x, z ) (z2 x) ( x < (z+1)2 ); – условие выхода из цикла
invB (x, k, s, n): ( k2x ) ( s= (k+1)2 ) ( n=2k+1 ) – инвариант цикла.
Определение набора условий корректности для всех путей между
соседними контрольными точками программы.
Путями между контрольными точками являются:
1 : от входа программы к точке разреза цикла (A – B);
2 : от точки разреза цикла через тело цикла обратно в точку разреза цикла (В – B);
3 : от точки разреза цикла через условие цикла к выходу программы
( B – C).
Тогда
U1 : P invB (x, k, s s+n, n)
( x 0 ) (k2 x ) ( s+n = (k+1)2 ) ( n=2k+1 ) )
( x 0 ) ( 02 x ) (0+1 = (0+1)2) ( 1=2*0+1 ) )
( x 0 ) ( ( 02 x ) (1 = 1) (1 = 1) );
U2 : invB (x, k, s, n) ((sx)
invB(x, k k+1, s s+n, n n+2))
( k2 x ) ( s = (k+1)2 ) ( n=2k+1 ) ((s x)
( (k+1)2 x ) ( s + n +2 = (k+2)2 ) ( (n+2) = 2*( k+1) +1) );
U3 : invB (x, k, s, n) ( ( s x ) invС ( x, z k) )
( k2 x ) ( s = (k+1)2 ) ( n=2k+1 ) ( ( s > x )
(k2 x) ( x < (k+1)2 )
Доказательство истинности условий U.
Истинность всех трех условий легко проверяется подстановкой.
4.1. Условие U1 – истина, так как
выражение ( x 0 ) ( ( 02 x ) (1 = 1) (1 = 1) )
(x 0) (0 x) (x 0) (0 x) (x < 0) (x 0) true
4.2. Преобразуем условие U2.
( k2 x ) ( s = (k+1)2 ) ( n=2k+1 ) ( (s x)
( (k+1)2 x ) ( s + n +2 = (k+2)2 ) ( (n+2) = 2( k+1) +1) )
( ( k2 x ) ( s = (k+1)2 ) ( n=2k+1 ) (s x) )
( (k+1)2 x ) ( s + n +2 = (k+2)2 ) ( (n+2) = 2( k+1) +1) )
Для доказательства истинности условия U2 нужно показать, что соотношения, образующие конъюктивные члены справа от знака импликации, следуют из соотношений, стоящих слева от знака импликации.
а) Поскольку x s и s = (k+1)2, то (k+1)2 x.
б) s+n+2 = (k+1)2 + 2k + 1 + 2 k2 + 2k+ 1+ 2k + 1 + 2 = (k+2)2
в) n+2 = 2 (k+1) +2 = 2 (k+1)+1
Следовательно, условие истинно.
4.3. Преобразуем условие U3.
( k2 x ) ( s = (k+1)2 ) ( n=2k+1 ) ( ( s > x )
(k2 x) ( x < (k+1)2 )
( k2 x ) ( s = (k+1)2 ) ( n=2k+1 ) ( s > x )
(k2 x) ( x < (k+1)2 )
Поскольку s > x и s = (k+1)2, то (k+1)2 > x и U3 – истина
Анализ завершенности последовательных программ
Особенность свойства завершенности программ состоит в том, что оно не зависит от постусловия программы, и для заданной программы полностью определяется предусловием. В общем случае формальный анализ свойства завершенности представляет весьма сложную проблему.
Имеются по меньшей мере две причины, по которым программа с заданным предусловием P может не завершиться:
обращение к частично определенной функции со значением аргументов вне области определения;
зацикливание.
Первая причина может приводить к аварийному завершению даже нециклических программ (например, при делении на нуль). Вторая причина присуща программам с итеративными циклами.
Ограничимся рассмотрением методов анализа завершения циклических вычислений без учета других возможных причин незавершения, т.е. предполагается, что любой нециклический оператор завершается и передает управление на его выход.
Наибольшее распространение получили два метода логического анализа завершения циклических вычислений:
метод Флойда;
метод счетчиков.
Метод Флойда
Этот метод может рассматриваться как дальнейшее развитие метода индуктивных утверждений. Основная идея метода состоит в том, чтобы с каждой контрольной точкой программы, лежащей на циклическом пути, связать некоторую частичную функцию, значения которой ограничены.
Для формализации этой идеи в достаточно общей форме введем понятие фундированного множества.
Пусть S – частично упорядоченное множество относительно бинарного отношения на его элементах, т.е. на множестве S для a, b и с S выполняются свойства:
антирефлексивности (a a) ;
антисимметрии a # b ((b a)) ;
транзитивности a b b # c a # c.
Множество S называется фундированным, если не существует бесконечной убывающей последовательности элементов из S.
Примеры фундированных множеств:
множество натуральных чисел с отношением < ;
множество * всех слов в алфавите , включая пустое слово с отношением w1 < w2, означающим что w1 есть собственное подслово w2.
Пусть Prgm – аннотированная программа, для которой методом индуктивных утверждений доказана частичная корректность. С каждой контрольной точкой r, лежащей на циклическом пути ( для этой точки существует обратный путь в точку r), свяжем частичную (ограничивающую) функцию r (x1, … , xn), принимающую значения в фундированном множестве S.
Для каждого пути между парой соседних контрольных точек r и t (r может совпадать с t), лежащих на циклическом пути, определим условие завершения в виде
W: ( invr(x1, …, xn) (Û(x1, …, xn)) (r(x1, …, xn)S
t((x1, …, xn))S r(x1, …, xn) t((x1, …, xn))))),
где U: invr(x1, …, xn) (Û(x1, …, xn)) invt((x1, …, xn)) – условие корректности метода индуктивных утверждений, – обратное преобразование, осуществляемое на пути в методе индуктивных утверждений, т.е.
U0 = Û(x1, …, xn) invt((x1, …, xn)), где (r – ограничивающая функция вида X1 X2 … Xn S, приписанная точке r.
Для доказательства завершенности программы методом Флойда может потребоваться усиление инвариантов, используемыхв доказательстве частичной корректности. В целом успех доказательства в значительной мере предопределяется искусством выбора ограничивающих функций .
Метод счетчиков
Идея этого метода состоит во введении в программу Prgm новых переменных-счетчиков, добавляемых по одной в каждый цикл программы. Переменная-счетчик должна инициализироваться перед входом в цикли увеличивать свое значение при каждом прохождении по циклу.
В преобразованной таким образом программе Prgm’ измененные инварианты циклов представляются в виде, содержащем условие ограниченности значений счетчиков функциями, зависящими только от входных переменных.
В отличие от метода Флойда этот метод не требует введения ограничивающих функций в контрольных точках. Переменные-счетчики рассматриваются как органическая часть программы, позволяющая логически выразить свойство завершенности в инвариантах цикла.
Преимущество этого метода перед методом Флойда состоит в том, что одни и те же инварианты используются при доказательстве частичной корректности и завершенности. Однако метод Флойда обладает большей общностью.
Успех доказательства завершенности в методе счетчиков определяется тем, удастся ли подобрать соответствующее условие ограниченности счетчика в инварианте цикла.
Этот метод, так же как и метод Флойда, требует творческого подхода программиста.