Малюнок 7. Геометрична інтерпретація довірчого інтервалу для істинного значення

З ймовірністю 95% фактичне значення параметра є між початковим ординатами цих прямих

Стандартна похибка оцінки коефіцієнта регресії B₁ обчислюється за формулою:

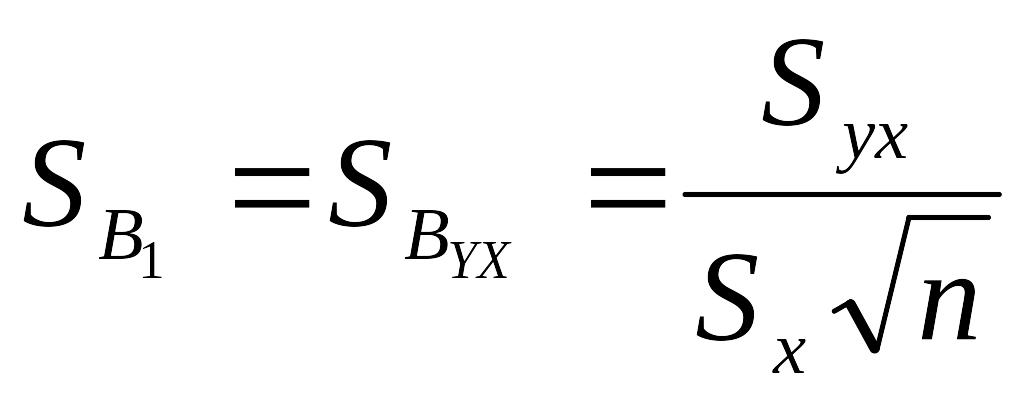
Гранична похибка оцінки коефіцієнта регресії B₀ обчислюється за формулою:

Геометрично довірчий інтервал інтерпретується парою прямих, що перетинаються у точці :

t_p =2,011 (користуємося таблицями розподілу Стьюдента), тоді:

= 2,011 * 0,0007= 0,0014

З ймовірністю 95% фактичне значення параметра b1 належить цьому проміжку:

:

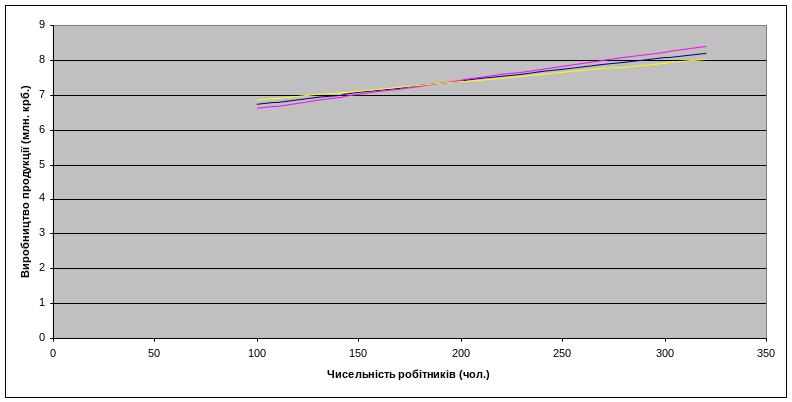
Малюнок 8. Геометрична інтерпретація довірчого інтервалу для істинного значення

14.Розрахунок вибіркової похибки моделі. Побудова довірчих інтервалів для середнього прогнозного значення результуючої змінної, геометрична інтерпретація

Знаючи вибіркові похибки параметрів моделі, можна знайти вибіркову похибку всієї моделі. Очевидно, що задача знаходження вибіркової похибки усієї регресії рівносильна задачі знаходження вибіркової похибки теоретичного значення результуючої змінної.

Для того, щоб представити це значення, запишемо ПЛКРМ у такому вигляді:

Згідно теореми про дисперсію двох незалежних випадкових величин маємо:

Дисперсія збігається з дисперсією при нульовому значення факторної ознаки, отже, шляхом математичних перетворень отримаємо таку формулу для обчислення стандартної вибіркової похибки моделі:

Стандартна вибіркова похибка моделі відображає похибку вибірки.

Стандартна вибіркова похибка моделі залежить від конкретного значення факторної ознаки і дає оцінку середнього значення результуючої змінної для цього значення факторної ознаки.

Гранична вибіркова похибка моделі

Геометрично, довірчий інтервал інтерпретується смугою між двома гіперболами:

Нехай x= 100 чол.

За даними обчислень:

За таблицями розподілу Стьюдента з рівнем значущості α=0,05 значення імовірнісного коефіцієнта tp=2,011.

Гранична вибіркова похибка моделі дорівнює:

(млн. крб.)

6,731 (млн . крб.)

Довірчий інтервал за заданого рівня імовірності:

6,1448≤ y ≤ 7,3172

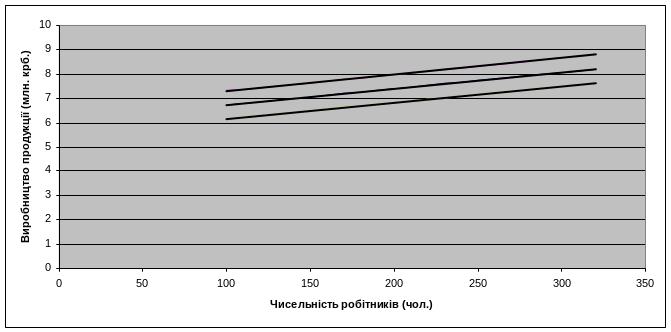
Малюнок 9. Геометрична інтерпретація довірчого інтервалу для фактичних значень результуючої змінної

15.Обчислення похибки індивідуального прогнозу. Побудова довірчих інтервалів для середнього прогнозного значення результуючої змінної, геометрична інтерпретація

Похибка оцінки індивідуального прогнозу обчислюється за формулою:

На основі стандартної похибки оцінки індивідуального прогнозу при заданому значенні ймовірності р можна визначити граничну похибку індивідуального прогнозу та побудувати довірчий інтервал для індивідуального прогнозу.

Гранична похибка знаходиться як добуток стандартної похибки на заданий імовірнісний коефіцієнт .

Для х = 100 чол.:

За таблицями розподілу Стьюдента з рівнем значущості α=0,05 значення імовірнісного коефіцієнта tp=2,011.

(млн. крб.)

Малюнок 10. Геометрична інтерпретація довірчого інтервалу індивідуального прогнозу