2. Алгоритм локализации точки

Предположим, что - вершинный ППЛГ является триангуляцией, в том случае, если он не триангуляция, его можно преобразовать в нее с помощью алгоритма представленного выше. Кроме того, окружим триангуляцию треугольной границей, путем построения охватывающего треугольника, и триангулирования области между этими двумя объектами.

Будем строить последовательность триангуляций , где, аполучается изпо следующим правилам:

1. Удалить некоторое множество внутренних несмежных вершин и инцидентные им ребра.

2. Вновь триангулировать многоугольники, образовавшиеся в результате удаления вершин и ребер.

Таким образом, не имеет внутренних вершин (т.е. состоит из одного треугольника).

Треугольники, главные объекты данного метода, будем обозначать буквой . Треугольникможет появляться во многих триангуляциях, однако условимся, чтопринадлежит триангуляции, еслисоздан на втором этапе построения.

Структура данных для поиска, узлам которой будут соответствовать треугольники, строится следующим образом: от узла соответствующего треугольникупроводится дуга к узлу соответствующему треугольнику, если при построениипослеимеем:

1. удаляется из 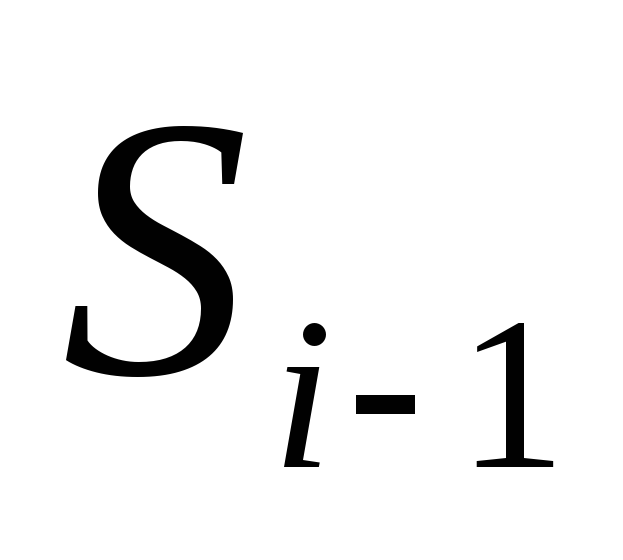на первом этапе.

2. создается в на втором этапе.

3. Ø.

Топология структуры представляется ориентированным ациклическим графом (см. рис.2.9.).Картинка неправильная

Рис.2.9. Последовательность триангуляций, и построенная структура данных поиска.

Отметим, что треугольники из не имеют исходящих дуг в, и только они обладают этим свойством.

Легко понять, как происходит локализация точки, в структуре данных поиска. Элементарной операцией является «принадлежность треугольнику», которая очевидно, выполняется за время . Начальный шаг состоит локализации пробной точки в триангуляции. Далее, если достигнут некоторый узел в структуре(т.е. точка локализована в соответствующем узлу треугольнике), то проверяется принадлежность пробной точки всем потомкам этого узла. Так как точка принадлежит только одному из потомков, то данный шаг выполняется с новым узлом и т.д., пока не будет достигнут узел, не имеющий потомков (т.е. точка локализована в одном из треугольников триангуляции). Запишем этот алгоритм в форме процедуры.

Procedure ЛокализацияТочки (z)

Begin

if (корень) then ОТВЕТ(вне);

else begin

= корень; //- вершина графа, которая соответствует

while (Ø) do

begin

repeat = очередная вершина из списка ;

until ;

;

end

ОТВЕТ();

end

End

Теперь обсудим очень важный аспект алгоритма построения последовательности триангуляций, а именно выбор множества удаляемых вершин на первом этапе построения триангуляции из, т.к. от этого выбора существенно зависит эффективность метода. Предположим, что можно выбрать это множество так, чтобы выполнялись следующие свойства (здесь черезобозначено число вершин в):

1. .

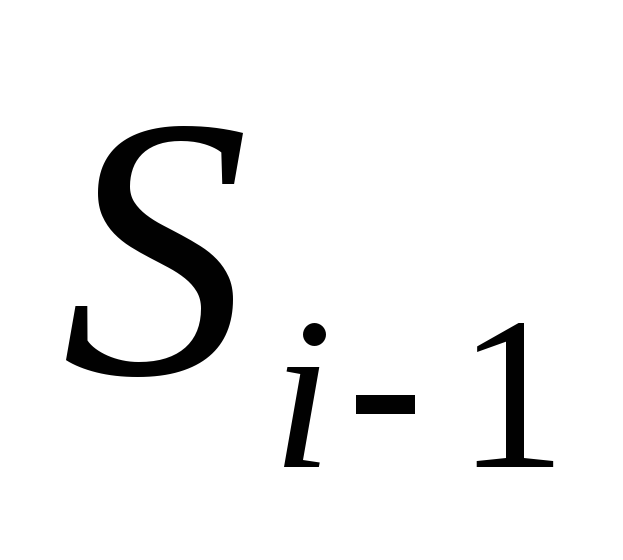2. Каждый треугольник изпересекается не более чем стреугольниками изи наоборот.

Следствием первого свойства является то, что поскольку при переходе откудаляется, по меньшей мере, фиксированная доля вершин. Это позволяет нам сделать вывод о том, что локализацию точки в структуреможно осуществить за время.

Теперь оценим память, отводимую для хранения узлов. Из теоремы Эйлера о плоских графах следует, что содержит менеетреугольников, т.е. ярус в, соответствующий, содержит менееузлов. Тогда общее число узлов вможно оценить следующим образом:

.

Из второго свойства следует, что каждый узел содержит не более указателей, тогда память отводимая под указатели не превосходит значения. Итого, суммарная требуемая память равна:

.

Теперь покажем, что существует критерий, удовлетворяющий обоим свойствам. Возьмем в качестве этого критерия следующий: «Удалить несмежные вершины со степенью меньше » (здесь- целое число, которое мы подберем позже). Порядок просмотра и, если необходимо, удаления этих вершин произволен: начинаем с любой из них, помечаем ее соседей (они не могут удаляться) и продолжаем, пока еще остаются непомеченные вершины.

Проверим выполнение первого свойства. Из формулы Эйлера для плоских графов, в частном случае триангуляции, ограниченной тремя ребрами, следует, что число вершин и число ребер связаны соотношением. Пока в триангуляции есть внутренние вершины (в противном случае задача тривиальна), степень каждой из трех граничных вершин не меньше трех. Поскольку существуетребер, а каждое ребро инцидентно двум вершинам, то сумма степеней всех вершин меньше. Отсюда сразу следует, что не менеевершин имеет степень меньше 12. Следовательно, пусть. Пусть- это число выбранных вершин. Поскольку каждой из них инцидентно не болееребер, а три граничные вершины не выбираются, то мы имеем:

.

Тогда число оставшихся вершин равно:

.

Следовательно , что доказывает справедливость первого свойства.

Выполнение второго свойства обеспечивается тривиально. Поскольку удаление вершины со степенью меньше приводит к образованию многоугольника с числом ребер менее , то каждый из удаленных треугольников пересекает не более новых треугольников.

Резюмируем:

Локализацию точки на - вершинном планарном подразбиении можно реализовать с помощью метода детализации триангуляции за времяс использованиемпамяти, есливремени ушло на предобработку.

Отметим, что данный метод обладает оптимальными характеристиками, в смысле требуемых ресурсов.