2. Метод цепей

В то время как в методе полос эффективность поиска достигается благодаря декомпозиции исходного подразбиения на трапеции, в методе цепей эта же цель достигается благодаря использованию монотонных многоугольников.

Ключевым в понятием, в обсуждаемом методе, является понятие цепи.

Определение. Цепьюназывается ППЛГ с вершинамии ребрами

Рассмотрим планарное подразбиение, определяемое ППЛГ . Предположим, что внайдена цепь(подграф) одного из следующих типов:

1. является циклом;

2. оба конца цепи илежат на границе бесконечной области (в этом случае дополнимс обоих концов полубесконечными параллельными ребрами).

Цепь каждого, из выше определенного, типа делит исходное подразбиение на две части. Далее, если удастся достаточно быстро определить по какую сторону от цепи лежит пробная точка (дискриминировать точку относительно цепи), то можно поискать новую разделяющую цепь, в нужной части плоскости.

В связи с этим возникает несколько следующих вопросов:

1. какова стоимость процедуры дискриминации точки относительно произвольной цепи;

2. существуют ли цепи, дискриминация относительно которых, проста;

3. какова трудоемкость поиска подходящей разделяющей цепи.

Ответ на первый вопрос очевиден, дискриминация точки относительно произвольной цепи является задачей не менее сложной, что и проверка принадлежности простому многоугольнику. Поэтому необходимо поискать более ограниченный класс цепей. Одним из таких классов является класс монотонных цепей.

Определение.называется монотонной по отношению к прямой, если любая прямая, ортогональная к, пересекаетровно один раз.

Отметим, что монотонная цепь относится ко второму типу определенных нами цепей, причем ортогональные проекции вершиннаупорядочены (см. рис.2.4.).

Теперь рассмотрим процесс дискриминации точки относительно таких цепей. Ясно, что проекцию пробной точкинаможно локализовать в единственном из интервалов. Затем, единственная проверка покажет, по какую сторону от прямой, несущей ребро, лежит пробная точка. Поэтому, если цепь содержитвершин, то дискриминация относительно такой цепи осуществима за время.

Рис.2.4. Примеры цепей: слева – общего вида; справа – монотонная по отношению к прямой .

Такая эффективность побуждает использовать монотонные цепи при локализации точек. Предположим, что существует некое множество Сцепей монотонных, относительно одной и той прямойи обладающих следующими свойствами:

1. ;

2. Цепи ине пересекаются.

Такое множество Cназывается полным множеством цепей графа. Отметим, что согласно второму свойству, цепи из полного множества упорядочены. Следовательно, можно применить кСдвоичный поиск, в котором элементарной операцией вместо простого сравнения чисел будет дискриминация точки относительно цепи.

Остается вопрос: можно ли построить полное множество цепей для произвольного ППЛГ ? Ответ на этот вопрос отрицательный[1]. Однако существует класс ППЛГ для которых построение полного множества цепей возможно, кроме того, оказывается что произвольный ППЛГ можно преобразовать в такой граф. При этом создается несколько новых «искусственных» областей, которые, тем не менее, не мешают эффективному решению задачи локализации. Определим такой класс ППЛГ.

Определение. Пусть- ППЛГ с множеством вершин, где вершины индексированы так, чтотогда и только тогда, когда. Вершина называется регулярной, если существуют такие целые, чтои- ребра графа. Говорят, что ППЛГрегулярен, если каждая из его вершин регулярна (за исключением двух крайних вершини) (см. рис. 2.5.).

Рис.2.5. Пример нерегулярного (слева) и регулярного (справа) ППЛГ.

Теперь покажем, что регулярный граф распадается на полное множество цепей, монотонных относительно оси ординат. Далее прямая будет считаться осью ординат.

Введем условную ориентацию ребер графа . Пусть ребро, ориентировано отк, если. Тогда можно говорить о множествахисоответственно входящих и исходящих ребер. Отметим, что оба этих множества не пусты для каждой из не крайних вершин, т.к. граф – регулярен. Тогда, для любой вершины, можно построить монотонную цепь отк[1]. Чтобы показать то, что построенные цепи удовлетворяют обоим свойствам из определенияС, введем понятие веса ребра:

- вес ребра- число цепей, которым принадлежит.

Кроме того, введем следующие обозначения:

Тогда надо только показать, что веса ребер можно выбрать таким, что:

1. 

2. .

Первое условие показывает, что каждое ребро принадлежит, по крайней мере, одной цепи (свойство 1), а второе гарантирует, что цепей проходят через, и их можно выбрать так, чтобы они не пересекались. Реализация условияможет быть достигнута, за два прохода по графу:

1. 

2. Первый проход (от к) даст нам;

3. Второй проход (от к) даст нам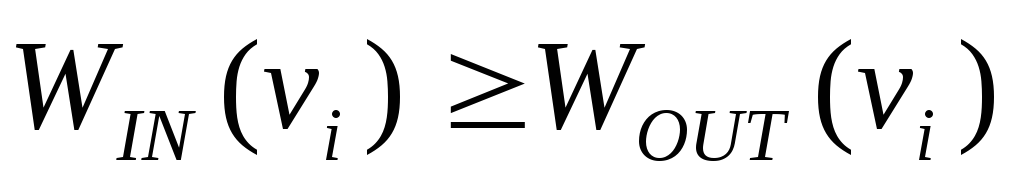, т.е. искомое выражение.

Запишем это в форме процедуры.

//

//

ProcedureБалансировкаПоВесуВРегулярномППЛГ

Begin

forдля каждого ребраdo;

fori= 2until do

begin

= сумма весов ребер, входящих в;

= крайнее слева ребро, исходящее из;

if ()then ;

end

for i = until 2 do

begin

= сумма весов ребер, исходящих из;

= крайнее слева ребро, входящее из;

if()then;

end

End

Очевидно, что данный алгоритм требует времени. Данную процедуру легко изменить так, что назначение ребер цепям происходило при реализации второго прохода.

Рис.2.6. Балансировка весов. Инициализация(слева), после двух проходов (справа).

Теперь обсудим преобразование произвольного ППЛГ в регулярный. И вновь нам поможет техника плоского заметания. А именно заметаем граф сверху вниз, чтобы регуляризовать вершины не имеющие исходящих ребер, а затем снизу вверх, чтобы регуляризовать вершины другого типа. В первом случае списком точек событий является последовательность вершин . Структура статуса заметающей прямой (которая будет реализована деревом, сбалансированным по высоте) задается упорядоченным слева на право списком номеров ребер ППЛГ, пересекающихся с заметающей прямой, и кроме того, с каждым интервалом между этими ребрами связана одна вершина (с минимальной ординатой в этом интервале). В процессе заметания для каждой встреченной вершиныреализуем следующие операции:

1. Локализуем (по абсциссе) в одном из интервалов в структуре данных статуса:

2. Корректируем структуру этого статуса:

3. Если нерегулярна, то добавляем ребро отдо той вершины, которая связана с интервалом, определенным в первой операции (см. рис.2.7.)

Рис.2.7. Пример нерегулярной вершины. Пунктирной линией показано регуляризующее ребро.

Отметим, что регуляризация -вершинного ППЛГ осуществима за времяблагодаря возможности начальной сортировки ординат его вершин и локализациивершин в структуре данных статуса за времядля каждой вершины.

Резюмируем:

-вершинный ППЛГ можно регуляризовать за времяс затратойпамяти.

Теперь проведем анализ метода цепей с точки зрения требуемых ресурсов.

Что касается предобработки, то она состоит из двух основных шагов:

1. Регуляризация ППЛГ (требует времени);

2. Балансировка по весу (требует времени).

Итого, предобработка требует времени.

Пусть ППЛГ распадается на цепей, причем самая «длинная» цепь содержитвершин. Тогда поиск в наихудшем случае потребуетвремени. Важно отметить то, что существуют такие ППЛГ, для которых эта оценка достижима (рис. 2.7.).

Рис.2.7. ППЛГ распадается на цепей,

каждая из которых, содержит ребер.

Теперь оценим требуемую память. Рассмотрим ППЛГ, изображенный на рис.2.8. Этот граф содержит в своем полном множестве цепей, в каждой из которыхребер, и кажется, что требуемая память будет квадратичной.

Рис.2.8. Граф содержитцепей, каждая из которых содержитребер.

Однако обратим внимание на то, как используются в алгоритме цепи. Конечно же, они используются в схеме двоичного поиска. Алгоритм двоичного поиска на полностью упорядоченном множестве индуцирует естественную иерархию на, представляемую двоичным деревом с корнем. Процесс поиска соответствует проходу в этом дереве от корня к листу. Если пронумеровать цепи, скажем, слева на права, то ребро, принадлежащее более чем одной цепи, будет принадлежать всем элементам множества (интервалу) последовательных цепей. Теперь предположим, цепи сопоставлены узлам дерева двоичного поиска. Если ребро, принадлежит нескольким цепям какого-то интервала, то существует единственный элемент С^*в этом интервале, который является общим предком для всех остальных элементов из этого интервала в дереве поиска. Пусть С – любой из этих остальных элементов. Тогда дискриминация пробной точки относительно С^*предшествует, в схеме двоичного поиска, дискриминации этой точки относительно С. Следовательно, реброможно отнести только к цепи С^*, и на самом деле оно будет отнесено к самой верхней в иерархии цепи из числа тех, которым оно принадлежит. Отметим, что число обходных указателей не превосходит числа ребер, и следовательно, полная структура данных поиска потребуетпамяти.

Резюмируем:

Локализацию точки на - вершинном планарном подразбиении можно реализовать с помощью метода цепей за времяс использованиемпамяти, есливремени ушло на предобработку.