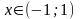Разложение функции в ряд Маклорена.
1. f (x) = ex.
Ряд
сходится к функции ех
на всей числовой оси.
2. f (x) = cos x.
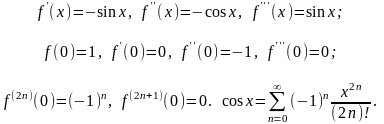
Аналогично
.
Ряд Маклорена для sin x и cos x сходится к ним на всей числовой оси, т. е. R = ¥.
3.
Согласно формуле суммы членов геометрической прогрессии со знаменателем х, |x|<1, имеем
Интегрируя левую и правую части равенства от 0 до х, при |x|<1 получаем
,
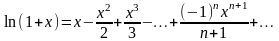Очевидно, область сходимости полученного ряда х ( ̶ 1; 1].
4. f (x) = (1+ x)α, где х > 1, α – любое действительное число.
Полученный ряд называется биномиальным.
При любом α данный степенной ряд сходится к функции (1+ x)α на (-1; 1).
5. f (x) = arctg x. Используем сумму геометрической прогрессии со знаменателем -t2 ( |t| < 1).
Интегрируя левую и правую части по t от 0 до х ( |x| < 1) получаем
Этот ряд сходится на интервале [ ̶ 1; 1].
6. f (x) = arcsin x.
Рассмотрим функцию
Разложим её в ряд, используя разложение ряда (1+ х)α при α = - ½
Это разложение справедливо при R = 1. Интегрируя левую и правую части от 0 до х находим
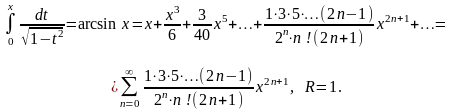
Замечание. Можно показать во всех полученных разложениях, что Rn(x)→0 при п → ¥.
Вычисление определенных интегралов с помощью рядов
Степенные ряды имеют разнообразные приложения. С их помощью с любой заданной точностью вычисляют значения функций (в частности значения π и e). Значительную роль играют степенные ряды в приближенных методах решений дифференциальных уравнений. Определенные интегралы от различных типов функций за малым исключением не вычисляются по формуле Ньютона – Лейбница, например,
и
др.
С помощью рядов находят приближенные значения таких определенных интегралов, которые или не выражаются через элементарные функции или сложны для вычислений. Среди них часто встречающиеся в практических приложениях математики.
Рассмотрим несколько примеров.
Пусть требуется вычислить интеграл
.
Здесь
первообразная от
не
является элементарной функцией. Для
вычисления этого интеграла разложим подынтегральную функцию в ряд
заменяя
в разложении
,тогда
.
Интегрируя обе части этого равенства в пределах от 0 до a, получим
С помощью этого равенства мы можем при любом a вычислить данный интеграл с любой степенью точности.
2.
Пусть требуется вычислить интеграл
Этот интеграл не берется в элементарных
функциях, поскольку первообразная
функции
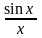не является элементарной. В то же время
эта первообразная легко выражается в
виде степенного ряда.
Из равенства
получаем
,
последний ряд сходится при всех значениях x.
Интегрируя почленно, получим
.
Сумма ряда вычисляется с любой заданной степенью точности при всех a.
Сводная таблица основных формул по теме «Функциональные ряды»
Понятие |
Определение, формула |
Функциональный ряд |
Ряд вида
u1+u2+u3+¼+un+¼= где u1,u2,…,un,…- функции переменной х.
|
Степенной ряд |
х0
≠0, а0+а1(х-х0)+…+аn(х-х0)n+…=
х0 = 0, |
Радиус ходимости |
По признаку Даламбера По радикальному признаку Коши
|
Ряд Тейлора |
f (x)= f (x0) + f ¢(x0) (х – х0) + + …+ + … |
Ряд Маклорена |
f
(x)= f
(0) + f ¢(0)
х +
|
Разложение функций по степеням х |
|
,
+ …+
+ …
ПРИМЕРЫ РЕШЕНИЯПРАКТИЧЕСКИХ ЗАДАЧ
Пример
1.Найти
область сходимости степенного ряда
.
Решение.
.
Найдем радиус сходимости ряда по
формуле (4):
.
Интервал
сходимости ряда (–5; 5). Исследуем
сходимость ряда на концах интервала
сходимости. При
получим ряд
,
который сходится по признаку Лейбница.
При
получим ряд
,
который сходится (это ряд Дирихле).
Область сходимости данного ряда
.
Пример 2. Определить интервал сходимости ряда
.
Решение. Применяя признак сходимости Даламбера, получим
Так
как предел не зависит от x
и меньше единицы, то значит ряд сходится
при всех значениях x.
.
Пример 3. Определить интервал сходимости ряда
.
Решение.
Этот ряд расходится при всех значениях
x,
кроме
,
так как
при
,
каково бы ни было x,
отличное от 0.
Пример
4.
Определить интервал сходимости ряда
.
Решение.
Здесь
.
Поэтому
.
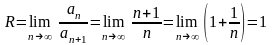Следовательно, данный ряд сходится на интервале (–1; 1).
Исследуем
поведение ряда на концах интервала
сходимости, то есть в точках
.
При
x
= 1 получаем гармонический ряд
(он расходится).
При
x
= –1 получаем ряд
.
Он сходится в силу признака
Лейбница .
Данный ряд сходится в любой точке
полуинтервала
и расходится вне его.
Пример
5. Разложить
в ряд по степеням х функцию
.
Воспользуемся
разложением
Полагаем
и получим
.
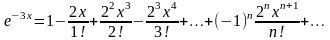Отсюда
.
Пример
6. Разложить
в ряд по степеням х функцию
.
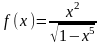Запишем
и воспользуемся разложением
Положим
,
.
Тогда
или
Пример
7. Разложить
функцию
в ряд по степеням
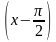
Воспользуемся разложением функции f (x) в ряд Тейлора
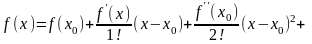
В последней формуле примем х0 = π / 2. Последовательно
Дифференцируя, найдём:
;
;
;
;
;
;
;
;
;
;
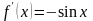и т.д., таким образом
Пример
8 Вычислить
определенный интеграл
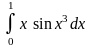с точностью
до 0,001
Решение.
Разложим
подынтегральную функцию в степенной
ряд. Воспользуемся
уже известным рядом:
.
Заменив в нем x
на
,
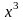получим
.
Умножим обе части равенства на
:
,
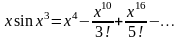отсюда
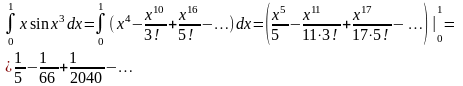
Замечаем, что третий член ряда по абсолютной величине меньше 0,001. Следовательно, для решения данной задачи, согласно признаку Лейбница, надо взять сумму первых двух членов, что обеспечит требуемую точность:
.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Найти область сходимости степенных рядов:
1.
;
2.
;
3.
;
4.
.
Ответы:1).
[ ̶ 1,5; 0,5] ; 2). ( ̶∞;+∞); 3). [ ̶
/3;
/3 ]; 4). [ ̶ 2; 2)
Разложить
в ряд по степеням
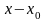функции:
6.
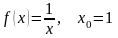7.
8
10.
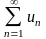