13.2. Функциональные ряды

Определение. Функциональным рядом называется ряд

. (13.2.1)

членами которого являются функции от x.

Давая x определенные числовые значения, мы получаем различные числовые ряды, которые могут оказаться сходящимися или расходящимися.

Определение. Функциональный ряд (13.2.1) называется сходящимся в точке х₀, если сходится числовой ряд

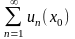
Определение. Совокупность тех значений x, при которых функциональный ряд сходится, называют областью сходимости этого ряда.

Область сходимости некоторых функциональных рядов можно найти с помощью известных достаточных признаков сходимости, установленных для рядов с положительными членами, например, признака Даламбера, радикального признака Коши.

Обозначим через сумму первых n членов ряда (13.2.1).Если этот ряд сходится и сумма его равна 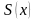, то её можно представить в виде

где 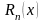есть сумма сходящегося ряда

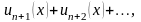
_{который называется n-м остатком функционального ряда (13.2.1),}

_{то есть}

Для всех значений x в области сходимости ряда имеет место соотношение

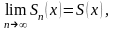
поэтому

то есть остаток сходящегося ряда стремится к нулю при .

13.3. Степенные ряды

Определение. Ряд вида

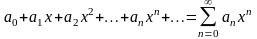(13.3.1)

называется степенным рядом, а числа а₀, а₁, а₂, ¼, а_п, ¼-коэффициентами степенного ряда.

Теорема Абеля.

1) Если степенной ряд (13.3.1) сходится при х=х₀ (х₀¹0), то он сходится, и притом абсолютно, для любых х удовлетворяющих условию |х|<|x₀|;

2) Если ряд (1) расходится при х=х₁, то он расходится для любых х, удовлетворяющих условию |х|>|x₁|.

Доказательство. 1) Так как по условию числовой ряд 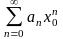сходится, то его общий член _{→ 0} при п →∞. Отсюда следует, что существует число М>0 такое, что все члены ряда по абсолютной величине меньше М ,т.е.

. (13.3.2)

Перепишем ряд (13.3.1) в виде

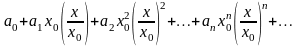
и рассмотрим ряд, составленный из абсолютных величин его членов

(13.3.3)

Члены ряда (13.3.3), в силу неравенства (13.3.2) меньше соответствующих членов ряда

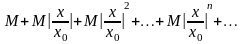(13.3.4)

При |х|<|x₀| ряд (13.3.4) представляет собой геометрическую прогрессию со знаменателем 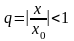и, следовательно, сходится. Так как члены ряда (13.3.3) меньше соответствующих членов ряда (13.3.4), то, по признаку сравнения, ряд (13.3.3) также сходится, а это значит, что ряд (13.3.1) сходится абсолютно.

2) По условию, в точке х₁ ряд (1) расходится. Докажем, что он расходится для любого х: |х|>|x₁|. Предположим обратное, т. е. допустим, что при некотором значении х, таком, что |х|>|x₁|, ряд (13.3.1) сходится. Тогда по только что доказанной первой части теоремы этот ряд должен сходится в точке х₁, т. к. |x₁|<|х|. Но это противоречит условию теоремы. Теорема доказана.

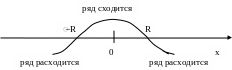
Следствие. Если ряд (13.3.1) сходится не при всех значениях х и не только в точке х=0, то существует число R>0 такое, что ряд абсолютно сходится при |х|<R и расходится при |х|>R. (без доказательства).

Определение. Радиусом сходимости степенного ряда называется такое число R, что для всех х: |х|<R, степенной ряд сходится, а для любого х: |х|>R, расходится.

Интервал (-R; R) называется интервалом сходимости. Множество точек, в которых ряд сходится, называется областью сходимости степенного ряда. Область сходимости есть интервал сходимости, который может включать один или оба его конца.

Замечание. 1) Если R=0, то ряд сходится в единственной точке х=0. Если R=¥, то ряд сходится при всех х.

2) При х= ±R ряд может, как сходится, так и расходится. Вопрос о сходимости ряда решается индивидуально для каждого конкретного ряда

Теорема (о способе определения радиуса сходимости).

Если существует

, (13.3.5)

то радиус сходимости ряда (13.3.1) равен

. (13.3.6)

Доказательство. Исследуем ряд (13.3.1) на сходимость по признаку Даламбера. По условию теоремы существует предел (13.3.5). Обозначим его . Тогда

.

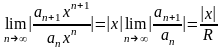При каждом значении х ряд становится числовым. Поэтому по признаку Даламбера ряд сходится, если 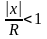, т. е. |х|<R. Следовательно, по достаточному признаку сходимости знакопеременного ряда ряд (13.3.1) сходится абсолютно при |х|<R.

При |х|>R этот ряд расходится, т. к.

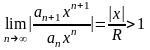
и его общий член 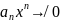при п®∞. Таким образом ряд сходится внутри

интервала (-R; R) и расходится вне его, при этом .

Замечание. Аналогичным образом, для определения интервала сходимости можно пользоваться радикальным признаком сходимости Коши. Тогда радиус сходимости ряда (1) определяется формулой

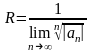, (13.3.7)

если предел, стоящий в знаменателе существует.