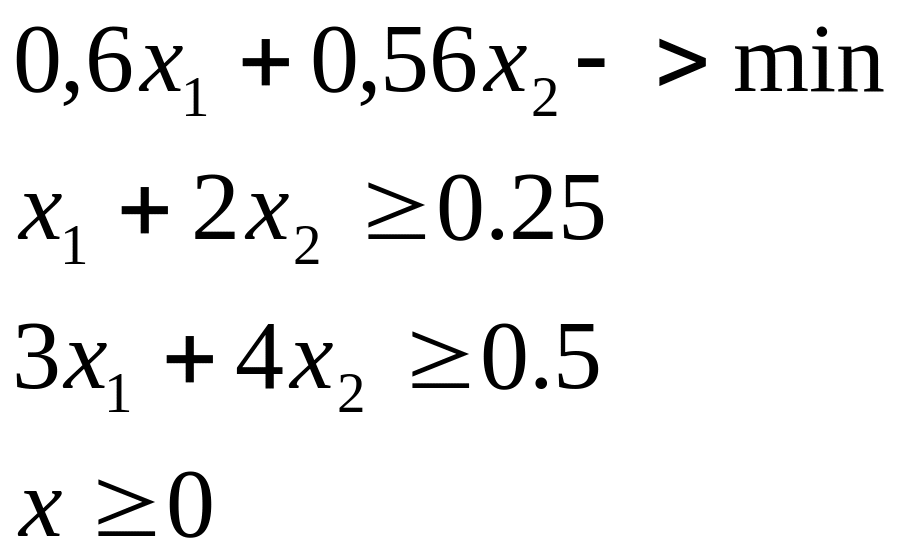- •Лабораторная работа № 4 Тема: «Модели и методы стохастического программирования»
- •Постановка задачи
- •Варианты
- •Форма отчета
- •Контрольные вопросы Тема: «Модели и методы стохастического программирования»
- •Пример 1.
- •Пример 2.
- •Пример 3.
- •Пример 4.
- •Примеры постановок задач стохастического программирования с р-ограничениями
- •3. Планирование добычи, обработки и хранения нефти
- •Дополнительные задания. Стохастическая тз (Юдин 35)
- •Список рекомендуемой литературы и интернет-ссылок
Пример 1.
1. Исходная постановка задачи.
ЗСтП с целевой функцией на минимум в KD-постановке и ограничениями в M-постановке. Решение - детерминированный вектор.
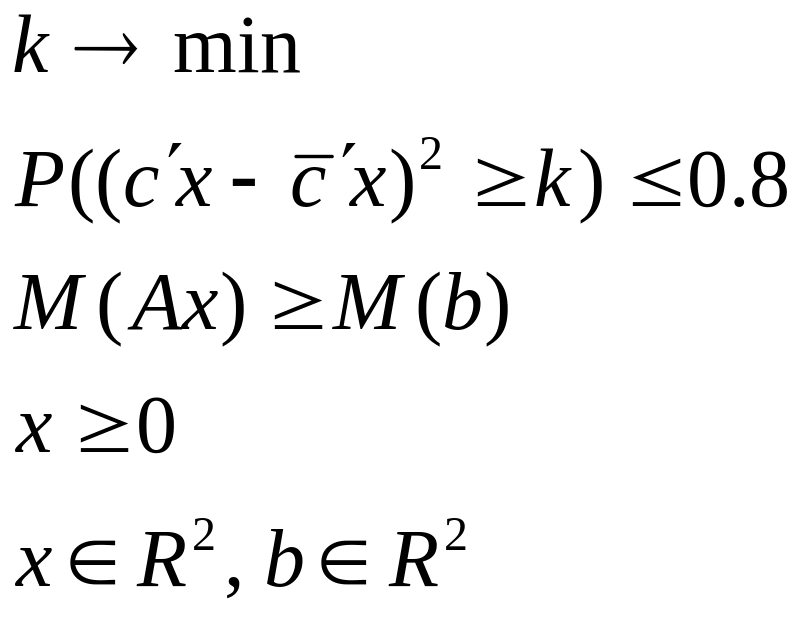
2. Параметры
А - детерминированная матрица:
![]() ,
- случайный вектор с заданными плотностями
вероятностей компонент,
,
- случайный вектор с заданными плотностями
вероятностей компонент,
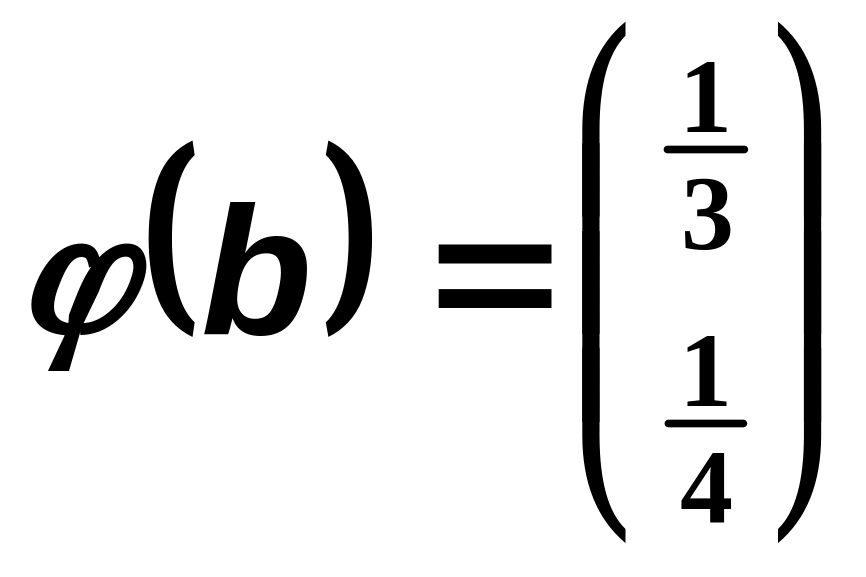 ,
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
,
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() и ковариационной матрицей
и ковариационной матрицей
![]() .
.
2. Детерминированный эквивалент ЗСтП.
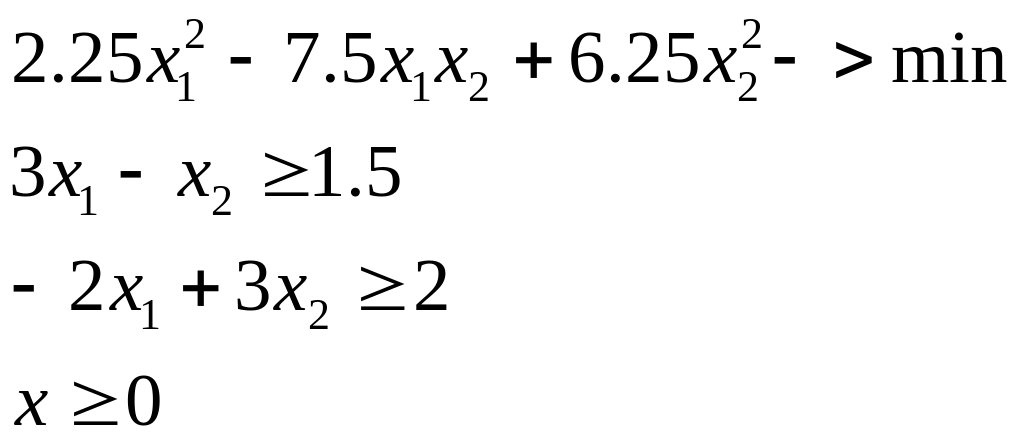 где
где
![]() .
.
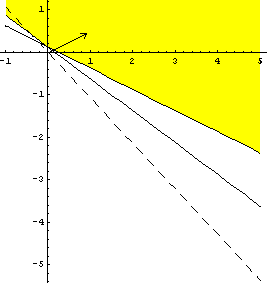
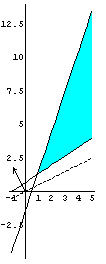
3. Графическое изображение множества планов детерминированного эквивалента ЗСтП .
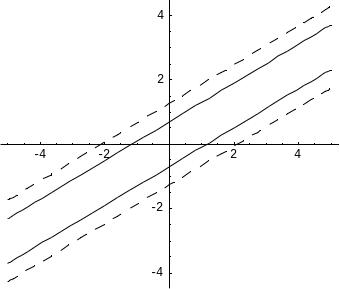
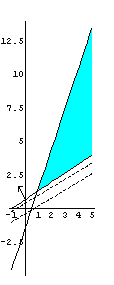
рис.1 рис.2
Т.к. на рис.2 линии уровня, соответствующие большему значению целевой функции (обозначены пунктиром) лежат выше линий уровня, соответствующих меньшему значению, то на рис.1 показан градиент.
4. Решение детерминированного эквивалента в пакете
![]()
5. Интерпретация полученного решения для исходной ЗСтП
При
![]() вероятность того, что дисперсия целевой
функции больше наименьшего
вероятность того, что дисперсия целевой
функции больше наименьшего
![]() ,
меньше
,
меньше
![]() и в среднем ограничения выполняются.
и в среднем ограничения выполняются.
6. Детерминированный эквивалент для исходной задачи с целевой функцией и ограничениями в М-постановках.
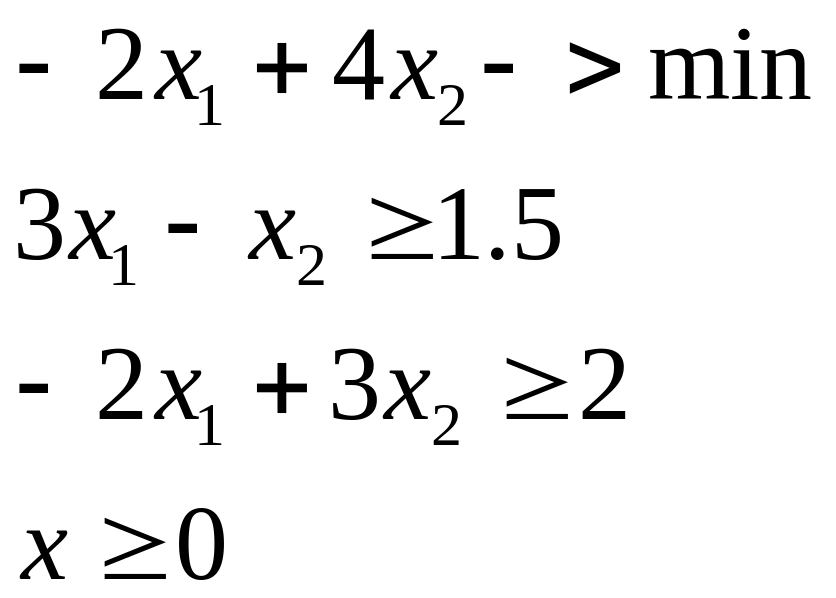
Пример 2.
1. Исходная постановка задачи.
![]()
![]()
![]()
![]()
2. Параметры
А - детерминированная матрица
![]() ,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
и дисперсиями.
,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
и дисперсиями.
![]() ,
,
![]() - нормально распределенные случайные
величины. ЗСтП с целевой функцией в
М-постановке и Р-ограничениями. Решения
в виде линейных решающих правил.
- нормально распределенные случайные
величины. ЗСтП с целевой функцией в
М-постановке и Р-ограничениями. Решения
в виде линейных решающих правил.
![]()
2. Детерминированный эквивалент ЗСтП.
![]()
В итоге исходная стохастическая задача сводится к выпуклой детерминированной задаче :
![]()
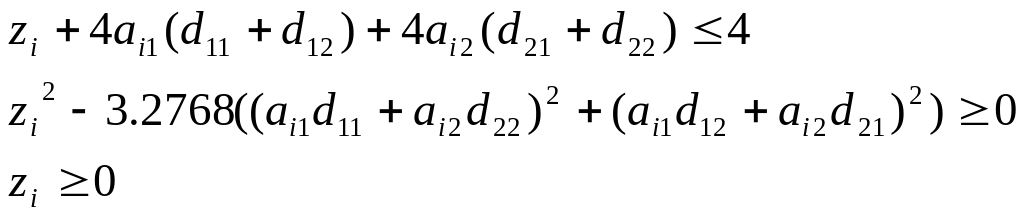
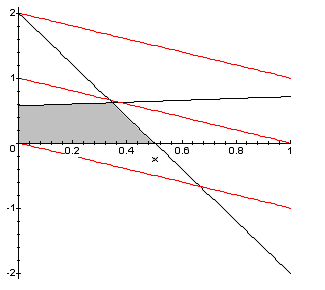
3. Графическое изображение множества планов детерминированного эквивалента ЗСтП .
4. Решение детерминированного эквивалента в пакете
![]() Значение целевой функции 4,35510177
Значение целевой функции 4,35510177
5. Интерпретация полученного решения для исходной ЗСтП
6. Детерминированный эквивалент для исходной задачи с целевой функцией и ограничениями в М-постановках.
![]()
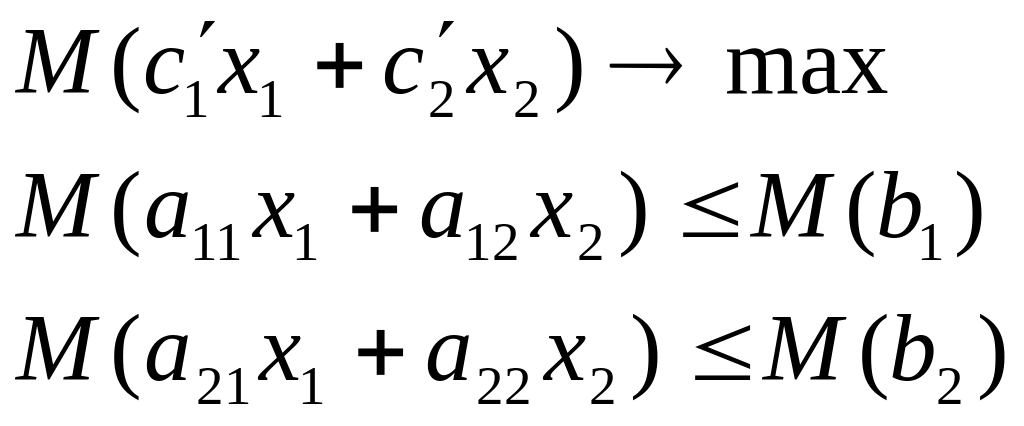
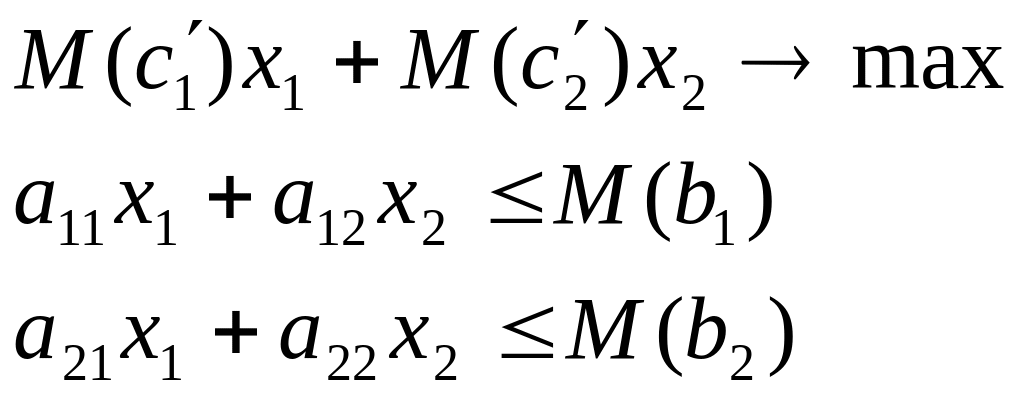
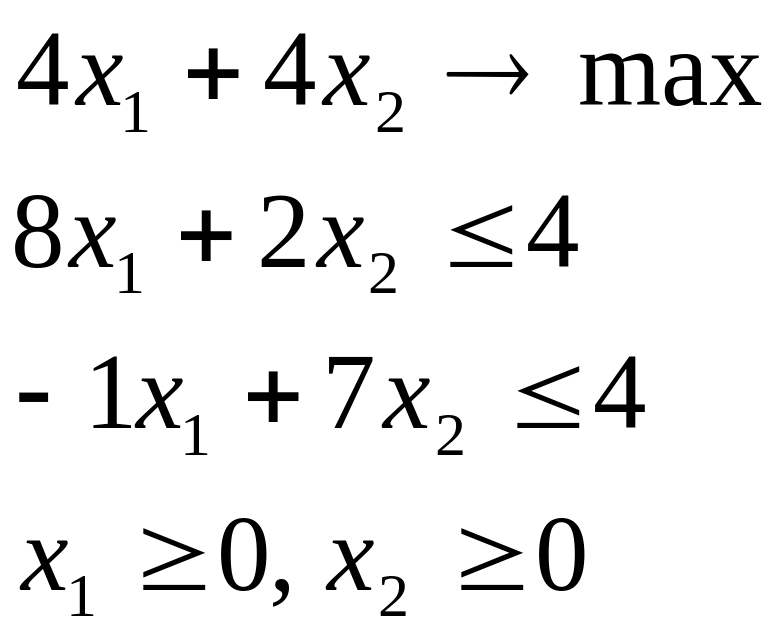
Решение :
x= |
0,34482759 |
|
0,62068966 |
Значение целевой функции 3,86206897
Пример 3.
1. Исходная постановка задачи.
ЗСтП с целевой функцией на минимум в KD-постановке и ограничениями в M-постановке. Решение - детерминированный вектор.
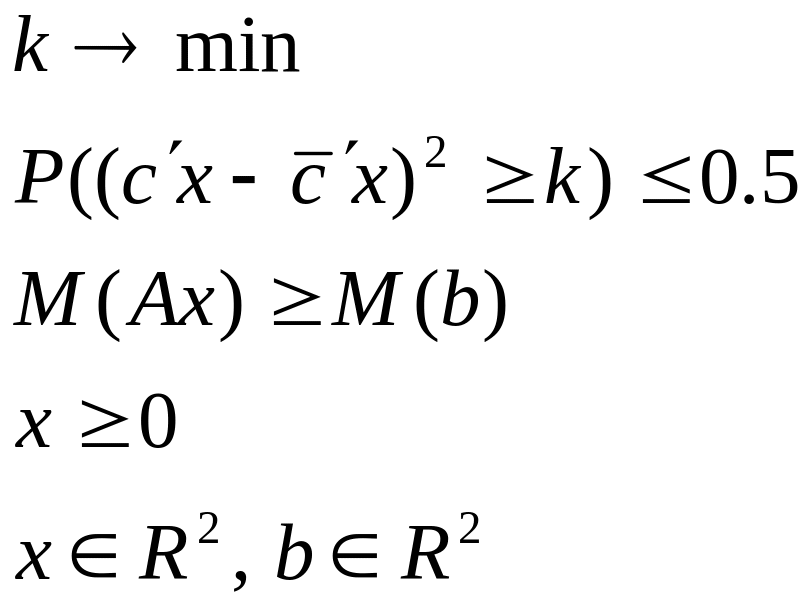
2. Параметры
А - детерминированная матрица:
![]() ,
- случайный вектор с заданными плотностями
вероятностей компонент,
,
- случайный вектор с заданными плотностями
вероятностей компонент,
![]() с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() и ковариационной матрицей.
и ковариационной матрицей.
![]()
2. Детерминированный эквивалент ЗСтП.
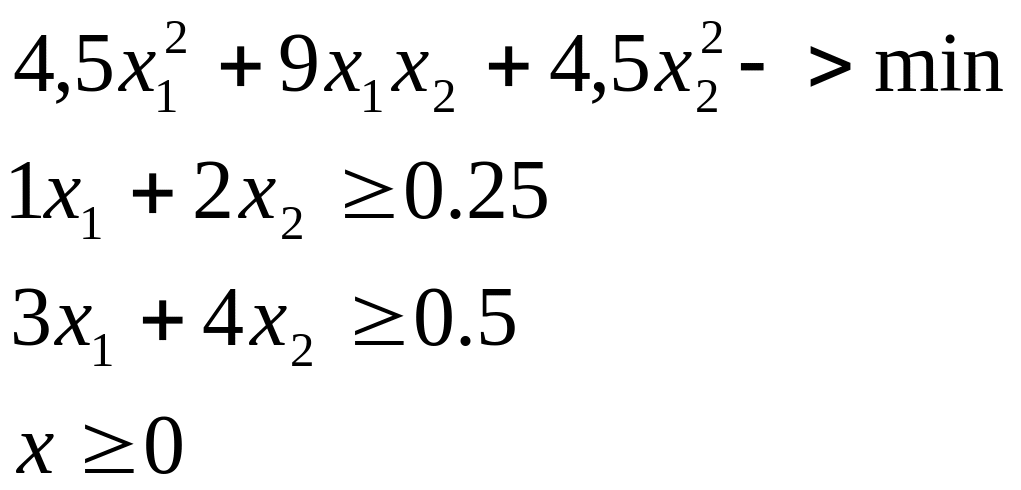 где
где
![]() .
.
3. Графическое изображение множества планов детерминированного эквивалента ЗСтП .
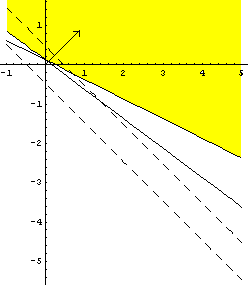 Рис1.
Рис1.
На рисунке линии уровня, которые соответствуют большему значению ц.ф. обозначены пунктиром. Линии уровня, которые соответствуют меньшему значению ц.ф. обозначены сплошной линией. Значит на Рис.1 изображен градиент.
Целевая функция:
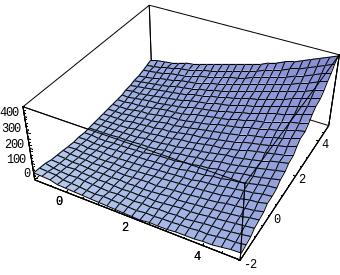
4. Решение детерминированного эквивалента в пакете
![]()
5. Интерпретация полученного решения для исходной ЗСтП
При
![]() вероятность того, что диперсия целевой
функции больше наименьшего
вероятность того, что диперсия целевой
функции больше наименьшего
![]() ,
меньше
,
меньше
![]() и в среднем ограничения выполняются.
и в среднем ограничения выполняются.
6. Детерминированный эквивалент для исходной задачи с целевой функцией и ограничениями в М-постановках.