
- •Лабораторная работа № 4 Тема: «Модели и методы стохастического программирования»
- •Постановка задачи
- •Варианты
- •Форма отчета
- •Контрольные вопросы Тема: «Модели и методы стохастического программирования»
- •Пример 1.
- •Пример 2.
- •Пример 3.
- •Пример 4.
- •Примеры постановок задач стохастического программирования с р-ограничениями
- •3. Планирование добычи, обработки и хранения нефти
- •Дополнительные задания. Стохастическая тз (Юдин 35)
- •Список рекомендуемой литературы и интернет-ссылок
Лабораторная работа № 4 Тема: «Модели и методы стохастического программирования»
Постановка задачи 1
Варианты 3
Форма отчета 7
Контрольные вопросы 8
Пример 1. 9
Пример 2. 10
Пример 3. 12
Пример 4. 15
Примеры постановок задач стохастического программирования с Р-ограничениями 16
Дополнительные задания. Стохастическая ТЗ (Юдин 35) 18
Список рекомендуемой литературы и интернет-ссылок 19
Цель: освоение постановок, моделей, методов и принципов оптимизации в условиях стохастической неопределенности, а также инструментальных средств для решения задач стохастического программирования.
Задачи:
Изучить основные постановки задач стохастического программирования
уяснить разницу между видами решений (детерминированное, решающее правило, *решающее распределение) задач стохастического программирования
освоить подходы к построению детерминированных эквивалентов основных постановок задач стохастического программирования
овладеть инструментальными средствами решения и анализа задач стохастического программирования.
Постановка задачи
Дана порождающая ЗЛП
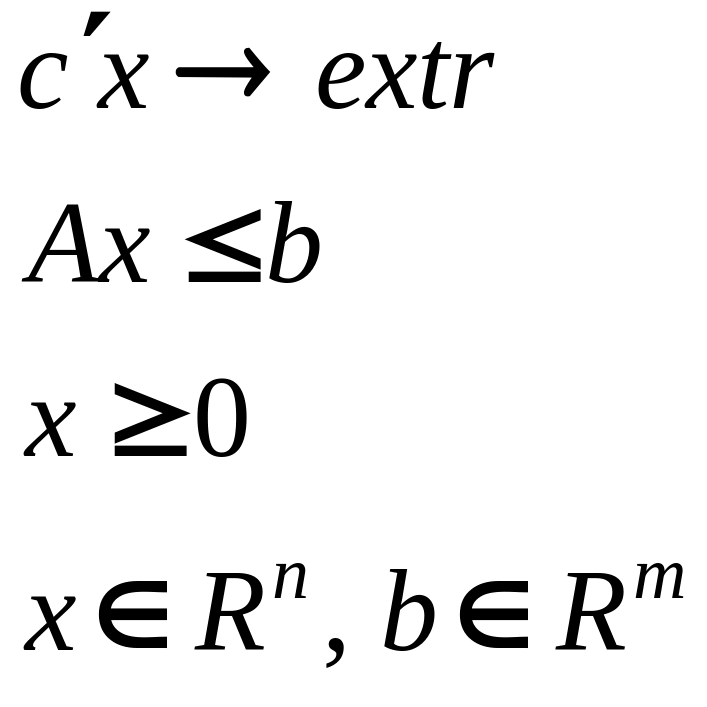
Для заданной порождающей ЗЛП при
![]()
составить задачу стохастического программирования (ЗСтП) (постановка согласно варианту),
построить ее детерминированный эквивалент (тип решения - согласно варианту),
графически изобразить множество планов детерминированного эквивалента и линии уровня ее целевой функции,
решить детерминированный эквивалент с помощью программных средств, дать интерпретацию полученного результата.
Построить детерминированный эквивалент для этой же задачи с целевой функцией и ограничениями в М-постановках, графически изобразить множество планов детерминированного эквивалента и линии уровня ее целевой функции, решить детерминированный эквивалент с помощью программных средств, дать интерпретацию полученного результата.
Сравнить решения в разных постановках. Сделать выводы.
исследовать вид множества планов детерминированного эквивалента при различных значениях
 -уровня
-уровняИсследовать зависимость решения от -уровня (от 0.5 до 0.9 с шагом 0.05)
При каких значениях оптимальное решение не меняется?
изучить распределение целевой функции на найденном оптимальном решении
* проверить условие доминирования ограничений (в стохастической постановке)
Недостающие параметры условия задать самостоятельно.
Варианты
В1 А - детерминированная
матрица
![]() ,
,
![]() - случайный вектор с заданными плотностями
вероятностей компонент:
- случайный вектор с заданными плотностями
вероятностей компонент:
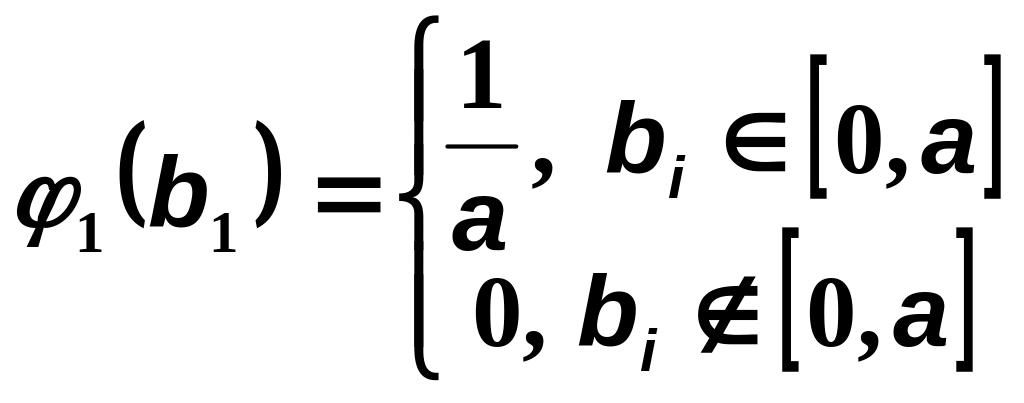 ,
,
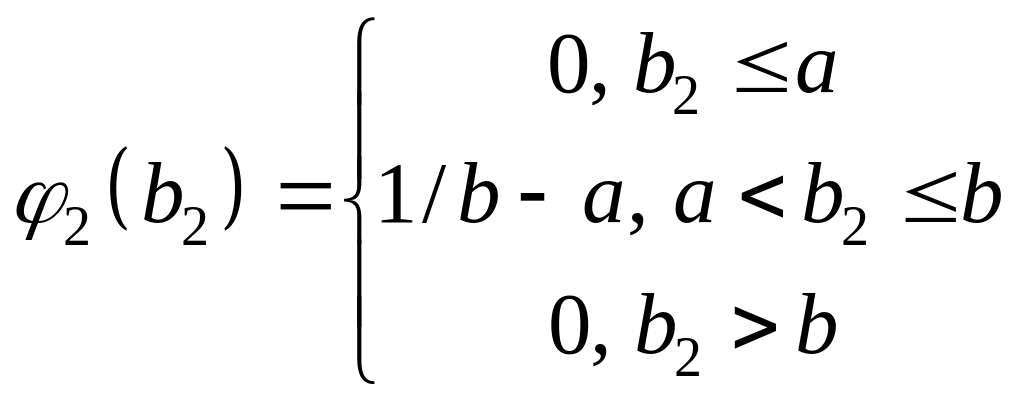 ,
,
![]() с - случайный вектор с известными
математическими ожиданиями компонент:
с - случайный вектор с известными
математическими ожиданиями компонент:
![]() .
.![]()
ЗСтП с целевой функцией в M-постановке и ограничениями в Р-постановке. Решение - детерминированный вектор.
В2 Компоненты матрицы
А и вектора
- независимые нормально распределенные
случайные величины с заданными
математическими ожиданиями
![]() ,
,
![]() ,
,
![]()
![]() ,
и дисперсиями
,
и дисперсиями
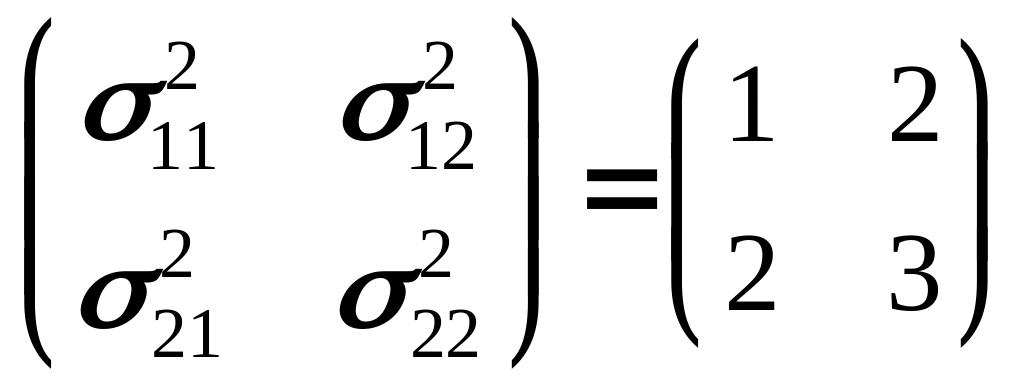 ,
,
![]() ,
с - детерминированный вектор,
,
с - детерминированный вектор,
![]() .
.
ЗСтП с ограничениями в Р-постановке. Решение - детерминированный вектор.
В3 А - детерминированная
матрица
![]() ,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]()
![]() и
дисперсиями
и
дисперсиями
![]() ,
,
![]() .
ЗСтП с целевой функцией на максимум в
V-постановке и ограничениями
в M-постановке. Решения в
виде линейных решающих правил.
.
ЗСтП с целевой функцией на максимум в
V-постановке и ограничениями
в M-постановке. Решения в
виде линейных решающих правил.
В4 А - детерминированная
матрица
![]() ,
- случайный вектор с заданными плотностями
вероятностей компонент
,
- случайный вектор с заданными плотностями
вероятностей компонент
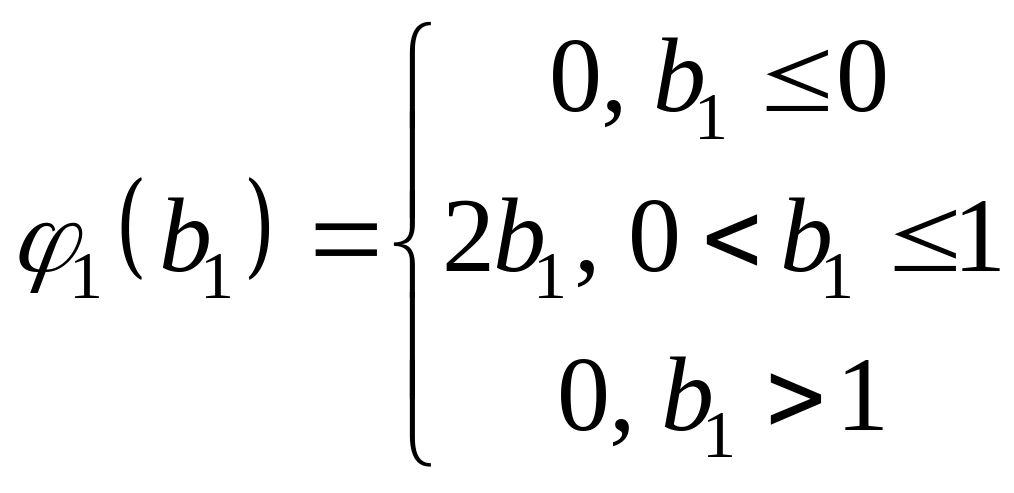 ,
,
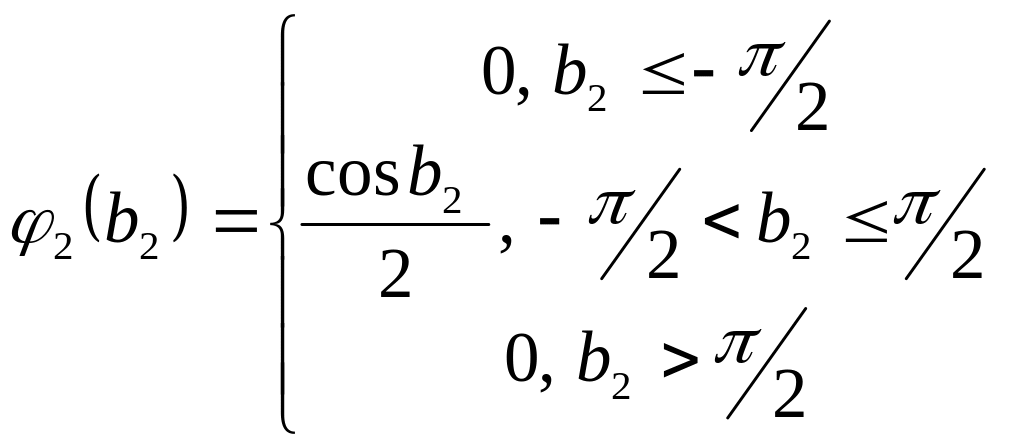 ,
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
,
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() и ковариационной матрицей
и ковариационной матрицей
![]() .
ЗСтП с целевой функцией в К-постановке
и ограничениями в Р-постановке. Решение
- детерминированный вектор.
.
ЗСтП с целевой функцией в К-постановке
и ограничениями в Р-постановке. Решение
- детерминированный вектор.
В5
А - детерминированная матрица
![]() ,
- случайный вектор с заданными плотностями
вероятностей компонент
,
- случайный вектор с заданными плотностями
вероятностей компонент
![]() ,
,
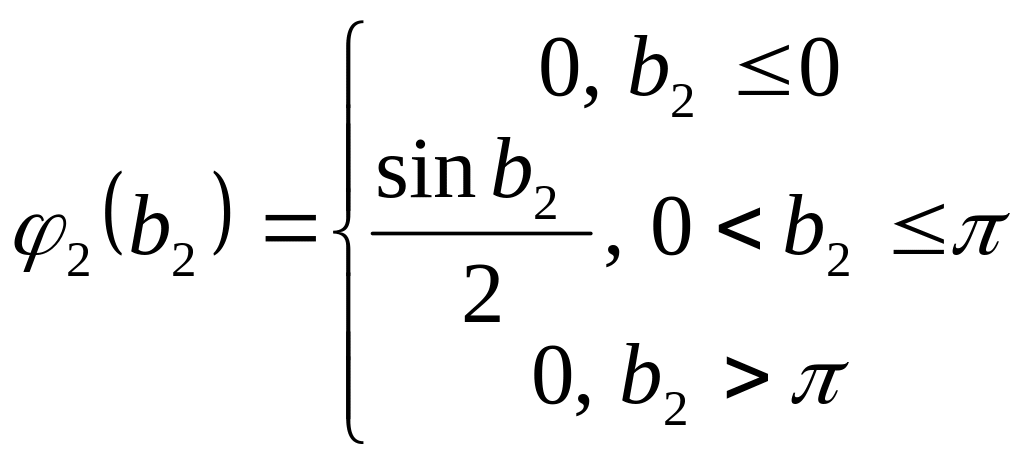 ,
,
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() и ковариационной матрицей
и ковариационной матрицей
![]() .
.
ЗСтП с целевой функцией на максимум в Р-постановке и ограничениями в Р-постановке. Решение - детерминированный вектор.
В6
А - детерминированная матрица
![]() ,
- случайный вектор с заданными плотностями
вероятностей компонент
,
- случайный вектор с заданными плотностями
вероятностей компонент
 ,
,
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
,
,
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() и ковариационной матрицей
и ковариационной матрицей
![]() .
ЗСтП с целевой функцией на минимум в
Р-постановке и ограничениями в
Р-постановке. Решение - детерминированный
вектор.
.
ЗСтП с целевой функцией на минимум в
Р-постановке и ограничениями в
Р-постановке. Решение - детерминированный
вектор.
В7
А - детерминированная матрица
![]() ,
- случайный вектор с заданными плотностями
вероятностей компонент
,
- случайный вектор с заданными плотностями
вероятностей компонент
![]() ,
,
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
,
,
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() и ковариационной матрицей
и ковариационной матрицей
![]() .
ЗСтП с целевой функцией на минимум в
P-постановке и ограничениями
в M-постановке. Решение -
детерминированный вектор.
.
ЗСтП с целевой функцией на минимум в
P-постановке и ограничениями
в M-постановке. Решение -
детерминированный вектор.
В8 А - детерминированная
матрица
![]() ,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() и
дисперсиями. ЗСтП с целевой функцией
на максимум в P-постановке
и ограничениями в Р-постановке. Решения
в виде линейных решающих правил.
и
дисперсиями. ЗСтП с целевой функцией
на максимум в P-постановке
и ограничениями в Р-постановке. Решения
в виде линейных решающих правил.
В9 А - детерминированная
матрица
![]() ,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
и дисперсиями
,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
и дисперсиями
![]() .
ЗСтП с целевой функцией на максимум в
М-постановке и ограничениями в
Р-постановке. Решения в виде линейных
решающих правил.
.
ЗСтП с целевой функцией на максимум в
М-постановке и ограничениями в
Р-постановке. Решения в виде линейных
решающих правил.
В10
А - детерминированная
матрица
![]() ,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() и
дисперсиями
.
ЗСтП с целевой функцией на максимум в
P-постановке и ограничениями
в Р-постановке. Решения в виде линейных
решающих правил.
и
дисперсиями
.
ЗСтП с целевой функцией на максимум в
P-постановке и ограничениями
в Р-постановке. Решения в виде линейных
решающих правил.
В11
А - детерминированная
матрица
![]() ,
- случайный вектор с заданными плотностями
вероятностей компонент, с - случайный
вектор, компоненты которого - коррелированные
между собой нормально распределенные
случайные величины с заданными
математическими ожиданиями
,
- случайный вектор с заданными плотностями
вероятностей компонент, с - случайный
вектор, компоненты которого - коррелированные
между собой нормально распределенные
случайные величины с заданными
математическими ожиданиями
![]() и ковариационной матрицей
.
ЗСтП с целевой функцией на минимум в
Р-постановке и ограничениями в
M-постановке. Решение -
детерминированный вектор.
и ковариационной матрицей
.
ЗСтП с целевой функцией на минимум в
Р-постановке и ограничениями в
M-постановке. Решение -
детерминированный вектор.
В12
А - детерминированная
матрица
![]() ,
- случайный вектор с заданными плотностями
вероятностей компонент, с - случайный
вектор, компоненты которого - коррелированные
между собой нормально распределенные
случайные величины с заданными
математическими ожиданиями
,
- случайный вектор с заданными плотностями
вероятностей компонент, с - случайный
вектор, компоненты которого - коррелированные
между собой нормально распределенные
случайные величины с заданными
математическими ожиданиями
![]() и
ковариационной матрицей
и
ковариационной матрицей
![]() .
ЗСтП с целевой функцией на минимум в
K-постановке и ограничениями
в P-постановке. Решение -
детерминированный вектор.
.
ЗСтП с целевой функцией на минимум в
K-постановке и ограничениями
в P-постановке. Решение -
детерминированный вектор.
В13
Строки матрицы А и
компоненты вектора
коррелированны, их компоненты - нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() ,
,
![]() и ковариационными матрицами
,
с - детерминированный вектор
и ковариационными матрицами
,
с - детерминированный вектор
![]() .
.
ЗСтП с ограничениями в Р-постановке. Решение - детерминированный вектор.
В14
А - детерминированная
матрица
![]() ,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() ,
и дисперсиями
,
и дисперсиями
![]()
![]() .
ЗСтП с целевой функцией на максимум в
P-постановке и ограничениями
в M-постановке. Решения в
виде линейных решающих правил.
.
ЗСтП с целевой функцией на максимум в
P-постановке и ограничениями
в M-постановке. Решения в
виде линейных решающих правил.
В15
А - детерминированная матрица
,
- случайный вектор с заданными плотностями
вероятностей компонент
,
,
с - случайный вектор, компоненты которого
- коррелированные между собой нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() и
ковариационной матрицей
и
ковариационной матрицей
![]() .
ЗСтП с целевой функцией на минимум в
P-постановке и ограничениями
в M-постановке. Решение -
детерминированный вектор.
.
ЗСтП с целевой функцией на минимум в
P-постановке и ограничениями
в M-постановке. Решение -
детерминированный вектор.
В16
А - детерминированная матрица
![]() ,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
и
дисперсиями
.
ЗСтП с целевой функцией на максимум в
V-постановке и ограничениями
в Р-постановке. Решения в виде линейных
решающих правил.
,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
и
дисперсиями
.
ЗСтП с целевой функцией на максимум в
V-постановке и ограничениями
в Р-постановке. Решения в виде линейных
решающих правил.
В17 А - детерминированная
матрица
![]() ,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
и дисперсиями
.
ЗСтП с целевой функцией на максимум в
М-постановке и ограничениями в
Р-постановке. Решения в виде линейных
решающих правил.
,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
и дисперсиями
.
ЗСтП с целевой функцией на максимум в
М-постановке и ограничениями в
Р-постановке. Решения в виде линейных
решающих правил.
В18
А - детерминированная матрица
,
,с
- независимые случайные векторы,
компоненты которых - нормально
распределенные случайные величины с
заданными математическими ожиданиями
![]() и
дисперсиями
и
дисперсиями
![]() .
.
ЗСтП с целевой функцией на максимум в P-постановке и ограничениями в Р-постановке. Решения в виде линейных решающих правил.
