Функции и графики

1. Общие понятия

2. Инъекция, сюръекция, биекция

3. График функции. Функции [x], {x}, |x|, sign x

4. Нахождение множеств точек на координатной плоскости, заданных набором условий

5. Линейная функция, график линейной функции

6. Четность/нечетность функции, ограниченность сверху/снизу, периодичность, промежутки монотонности

7. Преобразования графиков

1. Понятие функции

Функция – это некая штука, состоящая из ТРЁХ объектов (об этом не надо забывать!):

1. Множество, откуда действует функция (часто обозначается через Х)

2. Множество, куда действует функция (часто обозначается через У)

3. Собственно, само правило, которое КАЖДОМУ элементу Х сопоставляет РОВНО ОДИН элемент множества У

Заметьте еще раз, что КАЖДОМУ элементу Х что-то соответствует в множестве У. Причём ровно один элемент. Какие-то игреки могут соответствовать сразу нескольким иксам. А каким-то игрекам вообще может не повезти: ни одному иксу они не соответствуют

Заметьте также, что может быть очень много разных функций между одними и теми же Х и У

Множество Х называется областью определения функции, множество У – областью значений. Множество тех игреков, которым «повезло», называется образом функции (обозначается im f)

Обозначения и термины по поводу функции. У каждой функции, как, например, и у каждой переменной, есть своё имя. Например, «Здравствуйте, я – функция f» или «А я – функция g». В скобочках после функции указывается, от чего она берётся: или просто от какой-то абстрактной переменной – например, f(x) – или от конкретного числа – например, f(0). Тот икс, от которого мы выясняем значение, обычно называется аргументом функции, f(x) – значением функции f в точке x

3. График функции

Пусть есть функция f : X  Y. Графиком функции f называется множество пар (x,y), где х - из Х, у - из У, и при этом f(x) = y

Проще всего, конечно, график представлять себе графически. Ведь пару чисел удобно представлять себе одной точкой, с двумя координатами. Таким образом, график функции – это те точки, у которых игрековая координата равна значению функции от иксовой координаты

Из следующего графика хорошо видно, что f(2) = 0, f(0) = 1, а f(-3)=-1, хотя мы и не знаем самой функции f (например, не знаем, формулу, которой она задаётся)

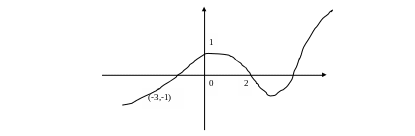
Горизонтальная ось называется осью абсцисс, вертикальная – осью ординат

Рассмотрим некоторые функции и их графики

Функция [x] (целая часть). Целая часть вещественного числа х — округление х до ближайшего целого в меньшую сторону. Целая часть числа также называется антье (от французского entier)

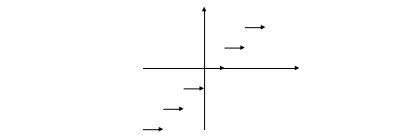
Функция {x} (дробная часть). Дробная часть вещественного числа х — разность между х и целой частью х. То есть, {x} = x – [x]

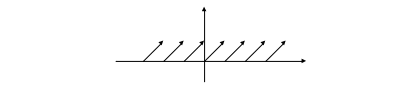
Функция sign x (сигнум, знак). sign x =

• -1, если х < 0

• 0, если х = 0

• 1, если х > 0

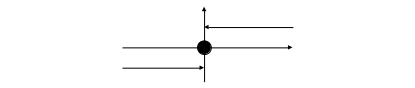
(Обратите внимание, что точка (0,0) лежит на графике. А также на то, что в Ворде сверхудобно рисовать)

Функция |x| (модуль, абсолютная величина). Модуль числа равен этому числу без учёта его знака. То есть, |x| =

• x, если x > 0 или х = 0

• -х, если х < 0

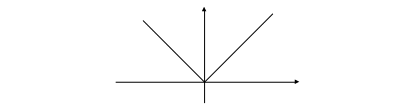
(Обратите внимание, что, если на осях выбран одинаковый масштаб (то есть, единичные отрезки на соях имеют одинаковую длину), то ветки графика будут идти под углом в 45^о к горизонтальной оси)

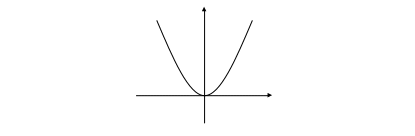
Функция x². Её графиком будет парабола

Функция 1/x. Её графиком будет гипербола

Общепринятые условные обозначения при рисовании графиков:

• Горизонтальная ось – ось аргументов, вертикальная ось – ось значений функции

• Если конец отрезка или луча не принадлежит графику, рисуют стрелочку

• Если графику не принадлежит какая-нибудь точка в середине линии, можно нарисовать две стрелочки, направленные друг к другу, а можно обвести выкалываемую из графика точку кружочком

После того, как вы нарисовали график, убедитесь, что он реалистичен (например, ветки не уходят на бесконечность у явно всюду ограниченной функции). Убедитесь, что каждая вертикальная прямая пересекает максимум одну точку графика (то есть, что у вас не получилось многозначной функции). Убедитесь, что у вас нет каких-то непонятных необъяснимых разрывов графика, и т.д.