1.1. Алгебра переключательных функций

Перейдем к рассмотрению свойств множества функций Р ⁽ⁿ⁾. Прежде всего отметим, что это множество является частично упорядоченным, поскольку для некоторых пар функций и можно установить отношение частичного порядка , если в векторе значений функции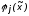 , вычисленном для всех возможных наборов , единицы стоят на всех тех местах, на которых они стоят в векторе значений функции , и может быть, еще на некоторых.

Определим на этом множестве операции нахождения наибольшей нижней и наименьшей верхней граней. Согласно определению, каждая переключательная функция из множества Р⁽ⁿ⁾ может принимать только значения из множества В ⁽²⁾. Если определить операции конъюнкции, дизъюнкции и отрицания с помощью табл. 1.3 и 1.4, то путем подстановки нетрудно убедиться, что все аксиомы булевой алгебры, оказываются справедливыми для этих операций. Например, подставляя вместо х вначале 0, а затем 1 в выражение , убеждаемся, что это равенство справедливо для любого х ÎВ⁽²⁾.

Таблица 1.3

							Таблица 1.4
0	0	0		0 1 1 1
0	1	0						0 1	1 0
1	0	0						1	0
1	1	1

Используя введенные операции, можно выполнять операции над значениями различных функций, соответствующих одному и тому же набору аргументов . Следовательно, на множестве Р⁽ⁿ⁾ можно определить операции конъюнкции и дизъюнкции, соответствующие нахождению наибольшей нижней и наименьшей верхней граней, следующим образом. Результатом конъюнкции функций и является функция , значения которой получаются путем вычисления конъюнкции значений Ù на всех наборах . Результатом дизъюнкции функций и является функция , значения которой получаются путем вычисления дизъюнкции значений Ú на всех наборах .

Таким образом, можно сделать вывод, что частично упорядоченное множество Р⁽ⁿ⁾ с определенными на нем операциями конъюнкции и дизъюнкции представляет собой алгебраическую решетку. Далее, можно утверждать, что при таком определении операций функция, принимающая значение 1 на всех наборах значений переменных , представляет собой наибольший элемент решетки - , а функция, принимающая значение 0 на всех наборах , - наименьший элемент решетки - .

Более того, для каждой функции в множестве Р ⁽ⁿ⁾ существует инверсный элемент , который вычисляется путем инвертирования каждого из значений функции .

Примеры выполнения операций, а также элементы и приведены в табл. 1.5.

Таблица 1.5

0 0 0	0	0	0	0	1	1	0
0 0 1	0	1	0	1	1	1	0
0 1 0	1	0	0	1	0	1	0
0 1 1	1	1	1	1	0	1	0
1 0 0	0	1	0	1	1	1	0
1 0 1	1	0	0	1	0	1	0
1 1 0	0	1	0	1	1	1	0
1 1 1	1	1	1	1	0	1	0

Для введенных операций конъюнкции и дизъюнкции для переключательных функций выполняются законы дистрибутивности. Справедливость этого утверждения основывается на свойствах операций конъюнкции и дизъюнкции, определенных на множестве В⁽²⁾. Выполнение законов дистрибутивности нетрудно проверить с помощью подстановки значений переменных.

Итак, множество переключательных функций Р⁽ⁿ⁾ с определенными на нем операциями конъюнкции, дизъюнкции, отрицания, наибольшим и наименьшим элементами представляет собой дистрибутивную решетку с дополнениями(булеву алгебру), которую называют алгеброй переключательных функций.

Последний вывод позволяет утверждать, что все аксиомы и теоремы, справедливые для булевых алгебр, должны выполняться в алгебре переключательных функций.

Переменную в функции называют несуществен­ной, если при любых значениях остальных переменных. Это означает, что изменение значения переменной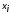 не изменяет значения функции, поэтому эту переменную можно исключить из числа аргументов и рассматривать заданную функцию как функцию, зависящую от n-1 переменной. Несущественные переменные можно не только удалять, но и добавлять к аргументам функции. Следовательно, если заданы две функции и , зависящие от разного числа переменных и k < I, то, добавляя к функции с меньшим числом аргументов (I – k) несущественных переменных, можно получить функции с одинаковым количеством аргументов k. Описанный прием позволяет рассматривать операции конъюнкции и дизъюнкции как операции, определенные на множестве переключательных функций, зависящих от различного числа аргументов.

С ростом числа переменных таблица истинности, задающая переключательную функцию, сильно усложняется. Чтобы избежать усложнения таблицы, в некоторых случаях функцию задают множеством номеров двоичных наборов, на которых она равна единице. Например, функция, приведенная в табл. 1.1., может быть задана в виде следующей совокупности двоичных наборов: или их десятичных эквивалентов: .