
- •3.1. Реализация переключательных функций в универсальном базисе Шеффера
- •3.2. Реализация переключательных функций в универсальном базисе Пирса
- •1. Системы счисления
- •1.1. Общие положения
- •1.2. Алгоритмы перевода чисел (ап) из одной системы счисления в другую
- •2. Двоично-кодированные системы счисления. Посимвольное и групповое кодирование
- •3. Требования к оформлению курсовой работы
- •4.Пример пояснительной записки курсовой работы
- •4.1. Построение таблицы преобразования чисел
- •4.2. Построение двоично-кодированной таблицы преобразования
- •4.3. Построение системы переключательных функций
- •4.4. Раздельная минимизация системы переключательных функций
- •4.5. Совместная минимизация системы переключательных функций, выбор универсального базиса
- •4.6. Преобразование в универсальный функциональный базис
- •4.7. Построение комбинационной схемы
4.Пример пояснительной записки курсовой работы
Исходные данные к курсовой работе:
Требуется
построить наиболее экономичную
комбинационную схему из элементов
одного из двух универсальных структурных
базисов («элемент Шеффера» - "И-НЕ",
П - «элемент Пирса» - "ИЛИ-НЕ"), для
варианта задания: преобразование чисел
в диапазоне от 0 до 8 из троичной системы
счисления ( )
в тринадцатеричную систему счисления
(
)
в тринадцатеричную систему счисления
( ).
Кодирование на входе и на выходе –
посимвольное «естественное».
).
Кодирование на входе и на выходе –
посимвольное «естественное».
4.1. Построение таблицы преобразования чисел
|
Десятичные значения |
Троичные значения |
Тринадцатеричные значения |
|
0 |
00 |
0 |
|
1 |
01 |
1 |
|
2 |
02 |
2 |
|
3 |
10 |
3 |
|
4 |
11 |
4 |
|
5 |
12 |
5 |
|
6 |
20 |
6 |
|
7 |
21 |
7 |
|
8 |
22 |
8 |
4.2. Построение двоично-кодированной таблицы преобразования
|
Десятичные Значения |
Троичные значения |
Тринадцатеричные значения | ||
|
Исходные |
Двоично–кодир.
|
Исходные |
Двоично-кодир.
| |
|
0 |
00 |
00 00 |
0 |
0000 |
|
1 |
01 |
00 01 |
1 |
0001 |
|
2 |
02 |
00 10 |
2 |
0010 |
|
3 |
10 |
01 00 |
3 |
0011 |
|
4 |
11 |
01 01 |
4 |
0100 |
|
5 |
12 |
01 10 |
5 |
0101 |
|
6 |
20 |
10 00 |
6 |
0110 |
|
7 |
21 |
10 01 |
7 |
0111 |
|
8 |
22 |
10 10 |
8 |
1000 |
4.3. Построение системы переключательных функций
Система ПФ строится на основании анализа двоично-кодированной таблицы преобразования.





Рис. П4.1.

Рис. П4.2.
4.4. Раздельная минимизация системы переключательных функций
А) Получение системы минимальных ДНФ


Рис. П4.3.
Минимальные покрытия:

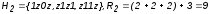

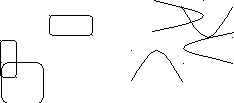
Рис. П4.4.
Минимальные покрытия:



B) Получение системы минимальных KНФ


Рис. П4.5.
Минимальные покрытия:

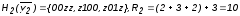


Рис. П4.6.
Минимальные покрытия:



Вывод:
при раздельной минимизации сложность
системы ДНФ ( )
меньше сложности системы КНФ (
)
меньше сложности системы КНФ ( )
на 3 единицы.
)
на 3 единицы.
4.5. Совместная минимизация системы переключательных функций, выбор универсального базиса
А) Получение минимальной совместной системы ДНФ


Рис. П4.7.


Рис. П4.8.
Обобщенная таблица минимальных покрытий
|
Ранг |
Импликанты |
|
|
|
|
|
2 2 2 2 3 3 2 |
1z1z 1z0z z1z1 z11z z100 001z z0z1 |
1 - - - - - - |
- 1 1 1 - - - |
- 1 - - 1 1 - |
- - - 1 1 - 1 |

В) Получение минимальной совместной системы KНФ


Рис. П4.9.


Рис. П4.10.
Обобщенная таблица минимальных покрытий
|
Ранг |
Импликанты |
|
|
|
|
|
1 1 3 3 2 2 2 2 2 |
zz0z 0zzz 000z z100 z01z z1z1 1z1z z11z z0z0 |
1 1 - - - - - - - |
- - 1 1 1 - - - - |
- - 1 - - 1 1 1 - |
- - - - - 1 - - 1 |
R=(3+3+2+2+2+2+2)+2+3+4+2=16+11=27
