
- •3.1. Реализация переключательных функций в универсальном базисе Шеффера
- •3.2. Реализация переключательных функций в универсальном базисе Пирса
- •1. Системы счисления
- •1.1. Общие положения
- •1.2. Алгоритмы перевода чисел (ап) из одной системы счисления в другую
- •2. Двоично-кодированные системы счисления. Посимвольное и групповое кодирование
- •3. Требования к оформлению курсовой работы
- •4.Пример пояснительной записки курсовой работы
- •4.1. Построение таблицы преобразования чисел
- •4.2. Построение двоично-кодированной таблицы преобразования
- •4.3. Построение системы переключательных функций
- •4.4. Раздельная минимизация системы переключательных функций
- •4.5. Совместная минимизация системы переключательных функций, выбор универсального базиса
- •4.6. Преобразование в универсальный функциональный базис
- •4.7. Построение комбинационной схемы
2. Двоично-кодированные системы счисления. Посимвольное и групповое кодирование
Для
представления чисел в произвольной
системе счисления с основанием
 с целью их хранения и обработки требуются
физические элементы, устойчивые и
надежно различаемые состояния которых
однозначно соответствуют символам из
алфавита системы счисления. Однако
решение этой задачи для произвольных
с целью их хранения и обработки требуются
физические элементы, устойчивые и
надежно различаемые состояния которых
однозначно соответствуют символам из
алфавита системы счисления. Однако
решение этой задачи для произвольных представляет собой сложнейшую научную
и техническую проблему. К этому нужно
добавить еще и необходимость развитого
математического аппарата, пригодного
для описания, анализа и синтеза дискретных
устройств на основе элементов с
представляет собой сложнейшую научную
и техническую проблему. К этому нужно
добавить еще и необходимость развитого
математического аппарата, пригодного
для описания, анализа и синтеза дискретных
устройств на основе элементов с состояниями.
состояниями.
Наиболее развита в настоящее время теория и практика построения дискретных устройств на основе двоичных элементов. В качестве математического аппарата используется хорошо разработанная теория булевой алгебры на множестве переключательных функций произвольного числа аргументов.
Переход к двоично-кодированному представлению позволяет строить схемы из двоичных элементов для обработки информации в произвольных позиционных системах счисления. Такие схемы без памяти, называемые комбинационными схемами (КСх), или в общем случае преобразователями кодов, можно использовать для преобразования чисел из одной системы счисления в другую.
При этом возможны два подхода к кодированию:
– посимвольное кодирование;
– групповое кодирование.
При
посимвольном
кодировании используются так называемые
двоично-кодированные системы счисления.
В таких системах каждому символу из
алфавита  сопоставляется оригинальная
(неповторяющаяся) кодовая комбинация
символов двоичного алфавита
сопоставляется оригинальная
(неповторяющаяся) кодовая комбинация
символов двоичного алфавита .
Минимальная длина такой кодовой
комбинации определяется соотношением
.
Минимальная длина такой кодовой
комбинации определяется соотношением .
Для так называемого «естественного»
посимвольного кодирования при
.
Для так называемого «естественного»
посимвольного кодирования при от 3 до 15 можно использовать табл. П.1.1.
Однако возможно и произвольное
посимвольное кодирование, задаваемое
табличным способом.
от 3 до 15 можно использовать табл. П.1.1.
Однако возможно и произвольное
посимвольное кодирование, задаваемое
табличным способом.
Пример
2.1
Рассмотрим двоично-кодированную троичную
систему счисления ( =3).
В соответствии с формулой для
=3).
В соответствии с формулой для при кодировании символов троичного
алфавита достаточно двух двоичных
разрядов. Соответствие символов троичного
алфавита и двоичных кодовых комбинаций
приведено в табл. П.2.1
при кодировании символов троичного
алфавита достаточно двух двоичных
разрядов. Соответствие символов троичного
алфавита и двоичных кодовых комбинаций
приведено в табл. П.2.1
Таблица П.2.1
|
Символы троичного алфавита |
03 |
13 |
23 |
|
“Естественное” двоичное кодирование |
00 |
01 |
10 |
|
Произвольное двоичное кодирование |
01 |
11 |
10 |
Тогда троичное число 122,100123 в «естественном» двоично-кодированном представлении будет иметь вид 011010,0100000110, а при произвольном – 111010,1101011110. После отбрасывания незначащих нулей получим 11010,010000011 и 111010,110101111 соответственно.
При
групповом
кодировании оригинальные (неповторяющиеся)
кодовые комбинации символов двоичного
алфавита
 сопоставляются
уже не отдельным символам кодируемого
алфавита, а группам изk
смежных
символов. В этом случае говорят о так
называемых системах счисления с
укрупненным основанием, определяемым
числом
сопоставляются
уже не отдельным символам кодируемого
алфавита, а группам изk
смежных
символов. В этом случае говорят о так
называемых системах счисления с
укрупненным основанием, определяемым
числом
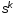 возможных
кодовых комбинаций в группе изk
символов исходного алфавита.
возможных
кодовых комбинаций в группе изk
символов исходного алфавита.
Разбиение на k - разрядные группы выполняется влево и вправо от запятой. При необходимости исходное число можно дополнить незначащими нулями для получения полных k - разрядных групп.
Пример
2.2
Рассмотрим групповое кодирование для
 иk
=
2. Максимальное целое десятичное число,
которое можно представить двумя троичными
разрядами, равно Sk-1=32-1=8.
При этом для представления десятичных
чисел от 0 до 8 используется 9 двухразрядных
троичных чисел из множества
{00,01,02,10,11,12,20,21,22}. Следовательно, укрупненное
основание в этом случае равно Sk=32=9.
В соответствии с формулой для
иk
=
2. Максимальное целое десятичное число,
которое можно представить двумя троичными
разрядами, равно Sk-1=32-1=8.
При этом для представления десятичных
чисел от 0 до 8 используется 9 двухразрядных
троичных чисел из множества
{00,01,02,10,11,12,20,21,22}. Следовательно, укрупненное
основание в этом случае равно Sk=32=9.
В соответствии с формулой для
 минимальная длина двоичной комбинации,
необходимой для укрупненного основания
минимальная длина двоичной комбинации,
необходимой для укрупненного основания ,
равна 4. Соответствие двухразрядных
троичных чисел и четырехразрядных
двоичных кодовых комбинаций приведено
в табл. П.2.2.
,
равна 4. Соответствие двухразрядных
троичных чисел и четырехразрядных
двоичных кодовых комбинаций приведено
в табл. П.2.2.
Таблица П.2.2
|
Двухразрядная
троичная
группа ( |
003 |
013 |
023 |
103 |
113 |
123 |
203 |
213 |
223 |
|
“Естественное” групповое кодирование |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
1000 |
|
Произвольное групповое кодирование |
1111 |
1110 |
1101 |
1100 |
1011 |
1010 |
1001 |
1000 |
0111 |
ПРИМЕЧАНИЕ. При произвольном групповом кодировании в табл. П.2.2 использованы двоичные комбинации, инверсные (обратные) “естественным” кодовым комбинациям.
Тогда троичное число 122,100123, предварительно дополненное незначащими нулями слева и справа для получения полных двухразрядных групп (0122,1001203), при “естественном” групповом кодировании будет иметь вид 00011000,001100010110, а при произвольном (инверсном) – 11100111,110011101001.
Пример 2.3 Пусть необходимо построить преобразователь кодов для преобразования чисел в диапазоне от 0 до 18 из троичной системы счисления в тринадцатеричную. В соответствии с формулой П1.2 для представления чисел в диапазоне от 0 до 18 достаточно трех троичных и двух тринадцатеричных разрядов. Табл. П2.3 устанавливает биекцию между двоично-кодированными представлениями чисел на входе и выходе преобразователя кодов.
ПРИМЕЧАНИЯ.
При посимвольном кодировании использованы табл. П.1.1., и табл. П2.1.
Старшие разряды полученных двоичных кодовых комбинаций, постоянные во всех строках таблицы, можно отбросить. В результате длина двоичных кодовых комбинаций при групповом кодировании для
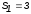 и
посимвольном “естественном” для
и
посимвольном “естественном” для может быть уменьшена с 8 до 6.
может быть уменьшена с 8 до 6.
Таблица П.2.3
|
|
|
| |||||||
|
Исход ные |
Двоично-кодированные |
Исход ные |
Двоично-кодирован ные («естественные») | ||||||
|
Посимвольное «естественное» |
Посимвольное произвольное |
Групповое «естественное» (k=2) |
Групповое «произвольное» (k=2)
|
|
| ||||
|
0 |
000 |
00 00 00 |
01 01 01 |
0000 1111 |
1111 1111 |
00 |
0000 0000 | ||
|
1 |
001 |
00 00 01 |
01 01 11 |
0000 1110 |
1111 1110 |
01 |
0000 0001 | ||
|
2 |
002 |
00 00 10 |
01 01 10 |
0000 1101 |
1111 1101 |
02 |
0000 0010 | ||
|
3 |
010 |
00 01 00 |
01 11 01 |
0000 1100 |
1111 1100 |
03 |
0000 0011 | ||
|
4 |
011 |
00 01 01 |
01 11 11 |
0000 1011 |
1111 1011 |
04 |
0000 0100 | ||
|
5 |
012 |
00 01 10 |
01 11 10 |
0000 1010 |
1111 1010 |
05 |
0000 0101 | ||
|
6 |
020 |
00 10 00 |
01 10 01 |
0000 1001 |
1111 1001 |
06 |
0000 0110 | ||
|
7 |
021 |
00 10 01 |
01 10 11 |
0000 1000 |
1111 1000 |
07 |
0000 0111 | ||
|
8 |
022 |
00 10 10 |
01 10 10 |
0000 0111 |
1111 0111 |
08 |
0000 1000 | ||
|
9 |
100 |
01 00 00 |
11 01 01 |
0001 0000 |
1110 1111 |
09 |
0000 1001 | ||
|
10 |
101 |
01 00 01 |
11 01 11 |
0001 0001 |
1110 1110 |
0A |
0000 1010 | ||
|
11 |
102 |
01 00 10 |
11 01 10 |
0001 0010 |
1110 1101 |
0B |
0000 1011 | ||
|
12 |
110 |
01 01 00 |
11 11 01 |
0001 0011 |
1110 1100 |
0C |
0000 1100 | ||
|
13 |
111 |
01 01 01 |
11 11 11 |
0001 0100 |
1110 1011 |
10 |
0001 0000 | ||
|
14 |
112 |
01 01 10 |
11 11 10 |
0001 0101 |
1110 1010 |
11 |
0001 0001 | ||
|
15 |
120 |
01 10 00 |
11 10 01 |
0001 0110 |
1110 1001 |
12 |
0001 0010 | ||
|
16 |
121 |
01 10 01 |
11 10 11 |
0001 0111 |
1110 1000 |
13 |
0001 0011 | ||
|
17 |
122 |
01 10 10 |
11 10 10 |
0001 1000 |
1110 0111 |
14 |
0001 0100 | ||
|
18 |
200 |
10 00 00 |
10 01 01 |
0010 0000 |
1101 1111 |
15 |
0001 0101 | ||
