1.2. Алгоритмы перевода чисел (ап) из одной системы счисления в другую

В этом разделе рассматриваются правила “ручного” перевода чисел из исходной системы счисления с основанием в результирующую систему счисления с основанием.

АП1. Перевод числа методом полинома (удобен для перевода в десятичную систему счисления).

1. Цифры и веса разрядов числа в системе представляются числовыми эквивалентами в системе.

2. Вычисляется сумма произведений полученных эквивалентов цифр и разрядных весов в соответствии с формулой П1.1.

Таблица П.1.1

Целые числа					Правильные дроби
=10	=2	=4	=8	=16	=10	=2	=4	=8	=16
0	0	0	0	0	0,03125	0,00001	0,002	0,02	0,08
1	1	1	1	1	0,0625	0,0001	0,01	0,04	0,1
2	10	2	2	2	0,125	0,001	0,02	0,1	0,2
3	11	3	3	3	0,1875	0,0011	0,03	0,14	0,3
4	100	10	4	4	0,25	0,01	0,1	0,2	0,4
5	101	11	5	5	0,3125	0,0101	0,11	0,24	0,5
6	110	12	6	6	0,375	0,011	0,12	0,3	0,6
7	111	13	7	7	0,4375	0,0111	0,13	0,34	0,7
8	1000	20	10	8	0,5	0,1	0,2	0,4	0,8
9	1001	21	11	9	0,5625	0,1001	0,21	0,44	0,9
10	1010	22	12	A	0,625	0,101	0,22	0,5	0,A
11	1011	23	13	B	0,6875	0,1011	0,23	0,54	0,B
12	1100	30	14	C	0,75	0,11	0,3	0,6	0,C
13	1101	31	15	D	0,8125	0,1101	0,31	0,64	0,D
14	1110	32	16	E	0,875	0,111	0,32	0,7	0,E
15	1111	33	17	F	0,9375	0,1111	0,33	0,74	0,F
16	10000	100	20	10	0,96875	0,11111	0,332	0,76	0,F8

Пример 1.1 Перевести число 11101,0101₂ (=2,=5,=4) в десятичную систему счисления (=10).

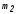Результат: 29,3125₁₀ (=10,=2,=4).

АП2. Перевод целого числа методом деления (удобен для перевода из десятичной системы счисления).

1. Представить основание системы счисления числовым эквивалентомв системе.

2. Делить нацело на сначала исходное число, а затем получаемые частные, запоминая на каждом шаге остатки от деления и заменяя их цифрами системы.

3. Пункт 2 выполнять до получения частного, равного нулю.

4. Записать полученные цифры в порядке, обратном их получению.

Пример 1.2 Перевести число 13₁₀ (=10,=2,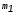=0) в двоичную систему счисления (=2).

Шаг 1. 13: 2 = 6 (1-е частное); 1-й остаток = 1 = (1)₂

Шаг 2. 6: 2 = 3 (2-е частное); 2-й остаток = 0 = (0)₂

Шаг 3. 3: 2 = 1 (3-е частное); 3-й остаток = 1 = (1)₂

Шаг 4. 1: 2 = 0 (4-е частное = 0); 4-й остаток = 1 = (1)₂

Результат: 1101₂ (=2,=4,=0). Обратный порядок следования цифр!

Пример 1.3 Перевести число 367₁₀ (=10,=3,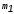=0) в шестнадцатеричную систему счисления (=16).

Шаг 1. 367: 16 = 22 (1-е частное); 1-й остаток = 15 = (F)₁₆

Шаг 2. 22: 16 = 1 (2-е частное); 2-й остаток = 6 = (6)₁₆

Шаг 3. 1: 16 = 0 (3-е частное = 0); 3-й остаток = 1 = (1)₁₆

Результат: 16F₁₆ (=16,=3,=0).

АПЗ. Перевод правильной дроби методом умножения (удобен для перевода из десятичной системы счисления).

1. Представить основание системы счисления числовым эквивалентомв системе.

2. Умножать сначала исходную дробь, а затем дробные части получающихся произведений на , запоминая на каждом шаге целые части произведений и заменяя их цифрами системы.

3. Пункт 2 выполнять до: а) получения дробной части, равной нулю (результирующая дробь конечна); б) получения числа цифр, обеспечивающих требуемую точность представления (результирующая дробь бесконечна, либо число значащих цифр превышает требуемую точность представления).

В случае б) результат округляется либо прекращением выполнения пункта 3 и фиксацией полученных цифр целой части произведений (округление усечением), либо выполнением еще одного дополнительного шага умножения, прибавлением к младшему разряду полученного результата величины 0,5 и окончательной фиксацией цифр этой суммы за исключением младшего разряда (симметричное округление).

4. Записать полученные цифры в порядке их получения.

Пример 1.4 Перевести дробь 0,6₁₀ (=10,=0,=1) в шестнадцатеричную систему счисления (=16) с точностью до 2-го знака после запятой.

Шаг 1. 0,6 * 16 = 9,6; (1-я дробная часть = 0,6); 1-я целая часть = 9 = (9)₁₆

Шаг 2. 0,6 * 16 = 9,6; (2-я дробная часть = 0,6); 2-я целая часть = 9 = (9)₁₆

Шаг 3. 0,6 * 16 = 9,6; (3-я дробная часть = 0,6); 3-я целая часть = 9 = (9)₁₆ Результат: а) 0,9(9)₁₆ (=16,=0,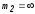) – бесконечная дробь – общее

решение;

б) 0,99₁₆ (=16,=0,=2) – усечение;

в) 0,9А₁₆ (=16,=0,=2) – симметричное округление.

АП4. Перевод смешанного числа.

Отдельно перевести целую часть числа методом деления (АП2), дробную часть методом умножения (АП3) и объединить полученные результаты, отделив их друг от друга запятой.

Пример 1.5 Перевести число 367,6₁₀ (=10,=3,=1) в шестнадцатеричную систему счисления (=16) с точностью до 2-го знака после запятой.

Перевод целой и дробной частей числа 367,6 был выполнен ранее в примерах 1.3 и 1.4. Результат получаем объединением результатов перевода целого числа 367 и правильной дроби 0,6 в смешанное шестнадцатеричное число.

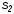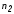Результат: а) 16F,9(9)₁₆ (=16,=3,) – бесконечная дробь – об-

щее решение;

б) 16F,99₁₆ (=16,=3,=2) – усечение;

в) 16F,9А₁₆ (=16,=3,=2) – симметричное округление.

АП5. Перевод числа методом "взвешивания” (удобен для перевода из десятичной системы счисления).

1. Представить основание системы счисления числовым эквивалентомв системе.

2. Определить значение из условияпо формуле

, (П1.2)

где ( ) – операция выделения целой части числа.

3. Выбрать значение из требований к точности представления результата.

4. Делить нацело сначала исходное число X, а затем полные остатки на веса разрядов новой системы , запоминая на каждом шаге частные и заменяя их цифрами системы .

Результат деления на вес 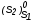дает младшую цифру целой части результата, за которой следует запятая (для).

5. Записать полученные цифры в порядке их получения, используя последнюю цифру для симметричного (если нужно) округления результата.

Пример 1.6 Перевести число 367,6₁₀ (=10,=3,=1) в шестнадцатеричную систему счисления (=16) с точностью до 2-го знака после запятой.

Из условия по формуле, выбираем значение=3. Из условия задачи значение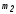= 2.

Шаг 1. 367,6: 16² = 1; (1-й остаток = 111,6); 1-е частное = 1 = (1)₁₆

Шаг 2. 111,6: 16¹ = 6; (2-й остаток = 15,6); 2-е частное = 6 = (6)₁₆

Шаг 3. 15,6: 16⁰ = 15; (3-й остаток = 0,6); 3-е частное = 15 = (F)₁₆

ПРИМЕЧАНИЕ. После этого шага в записи числа должна быть запятая!

Шаг 4. 0,6: 16^-1 = 9; (4-й остаток = 0,0375); 4-е частное = 9 = (9)₁₆

Шаг 5. 0,0375: 16^-2 = 9; (5-й остаток = 0,00234375); 5-е частное = 9 = (9)₁₆

Шаг 6. 0,00234375: 16^-3 = 9; (6-й остаток = 0,00014648442);

6-е частное = 9 = (9)₁₆

Результат: а) 16F,9(9)₁₆ (=16,=3,) – бесконечная дробь – об-

щее решение;

б) 16F,99₁₆ (=16,=3,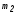=2) – отбрасывание младших

разрядов;

в) 16F,9А₁₆ (=16,=3,=2) – симметричное округление.

АП6. Перевод числа из S₁ в систему счисления с основанием (k 2) методом замены.

1. Цифры исходного числа разбить на группы из k цифр влево и вправо от запятой.

2. Крайнюю левую группу в целой части и крайнюю при необходимости правую в дробной части дополнить нуля­ми.

3. Заменить каждую группу эквивалентной цифрой .

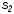Пример 1.7 Перевести число 11011,10101₂ ((=2,=5,=5) в восьмеричную (=8) и шестнадцатеричную (=16) системы счисления.

(11011,10101)₂ = (11 011,101 01)₂ = (011 011,101 010)₂ = (33,52)₈

(11011,10101)₂ = (1 1011,1010 1)₂ = (0001 1011,1010 1000)₂ = (1B,A8)₁₆

АП7. Перевод числа из системы счисления с основанием

(k 2) в систему с основанием S₂ методом замены.

Каждую цифру исходного числа заменить соответствующим k-разрядным эквивалентом, незначащие нули слева от старшего и справа от младшего разрядов опустить.

Пример 1.8 Перевести числа 371,54₈ (=8,=3,=2) и 6F,7C₁₆(S₁=16,n₁=2,m₂=2) в двоичную (=2) систему счисления.

(371,54)₈ = (011 111 001,101 100)₂ = (011111001,101100)₂ = (11111001,1011)₂

(6F,7C)₁₆ = (0110 1111,0111 1100)₂ = (01101111,01111100)₂ = (1101111,011111)₂