1. Системы счисления

Цель раздела: изучить представление чисел в позиционных системах счисления и способы их перевода из одной системы счисления в другую.

1.1. Общие положения

Система счисления – это способ представления чисел с помощью множества специальных символов, называемых цифрами и образующих алфавит системы счисления. Все множество систем счисления делится на два подмножества – непозиционных и позиционных систем счисления.

Классическим примером непозиционной системы счисления является римская система счисления, использующая алфавит , с символами (цифрами) которого связаны следующие значения:I=1, ,,,,, 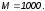Натуральные числа записываются в этой системе счисления при помощи комбинации этих цифр, причем не допускается четырехкратное повторение подряд одной и той же цифры. Если меньшая цифра стоит перед большей, то меньшая вычитается из большей. Таким образом, ставится соответственно переддля обозначения чисел 9, 90, 900 и переддля обозначения чисел 4, 40, 400. Поэтому, при построении числа в римской системе счисления можно забыть о правиле вычитания, приняв числаIV, IX, XL,… за одну цифру. Например, в записях исимволы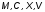независимо от их позиции в записи имеют “вес” 1000, 100, 10 и 5 соответственно. Однако символимеет различный вес: в комбинацииVI он имеет вес 1, тогда как в комбинации IV этот же символ имеет вес -1. С учетом этого записи иможно рассматривать как числа 2324 и 2326 соответственно. Очевидно, максимальное число в этой системе имеет вид, что соответствует значению1000*3+500*3+100*3+50*3+10*3+5*3+4=3000+1500+300+150+30+15+4=3999.

В позиционных системах счисления значение цифры в записи числа определяется ее позицией в последовательности цифр числа, поскольку с каждой позицией (разрядом) числа связывается определенный "вес". Алфавит системы счисления – множество из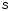цифр, каждая из которых обозначает определенное целое число. ЧислоD записывается в виде последовательности цифр, , в которой изображение дробной части от целой отделяется запятой:

Разряды – позиции цифр в числе – удобно нумеровать положительными числами влево от запятой и отрицательными числамивправо от запятой. Номераразрядов образуют множествоP={n-1,…2,1,0,-12,-3,…,-m}.

Записи числа D соответствует значение

где W_{i ,} W _j – веса соответствующих целых и дробных разрядов числа.

Особое место среди позиционных систем счисления занимают системы, в которых веса разрядов образуют геометрическую прогрессию со знаменателем , называемымоснованием системы счисления. В этом случае вес разряда является степенью основания системы счисления, причем показатель степени соответствует номеру разряда – элементу множества P: Значение числа определяется как взвешенная сумма значений цифр, т.е. сумма произведений цифр на их веса:

(П1.1)

В дальнейшем под значением числа будем понимать привычный нам десятичный эквивалент числа в системе счисления с произвольным основанием. Например, десятичное число 513,79 () может быть представлено в виде суммы:

D₁₀=(513,79)₁₀=(510²+110¹+310⁰+710^-1+910^-2)₁₀

Однако, если ту же символьную строку 513,79 интерпретировать как двадцатеричное число (), то его значение будет:

В табл. П.1.1 приведены примеры представления чисел в системах счисления с различными основаниями (2, 4, 8, 10, 16). В левой части таблицы показаны примеры представления целых чисел от 0 до 16. Жирным курсивом в каждом столбце выделен алфавит соответствующей системы счисления. В правой части таблицы показаны примеры представления правильных дробей с шагом 1/16= 0,0625. Исключение – первая и последняя строки, где представлены дроби 1/32= 0,03125 и 31/32= 0,96875. Примеры представления смешанных чисел нетрудно получить объединением соответствующих целых и дробных частей с одинаковым основанием системы счисления. 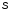Разрядность числа определяется количеством цифр в записи числа с отброшенными левыми незначащими нулями в целой части и правыми незначащими нулями в дробной части.