Лекція 3. Деякі застосування комплексних чисел

12. 1. Синусоїдальні величини

Коливання в електричному контурі описуються диференціальними рівняннями другого порядку розв’язок такого рівняння має вигляд

,

де — час, —амплітуда коливань, — частота коливань, пов’язана з періодом співвідношенням , — фаза.

Змінний струм, сила якого , в кожен момент часу має одне і теж значення у всьому ланцюгу. Це значення визначається, зокрема, формулою

. (40)

Струм, сила якого визначається формулою (40), називається синусоїдальним.

Дамо просте геометричне зображення синусоїдальних величин однієї і тієї ж частоти .

Розглянемо систему координат, в якій вісь — це вісь часу .

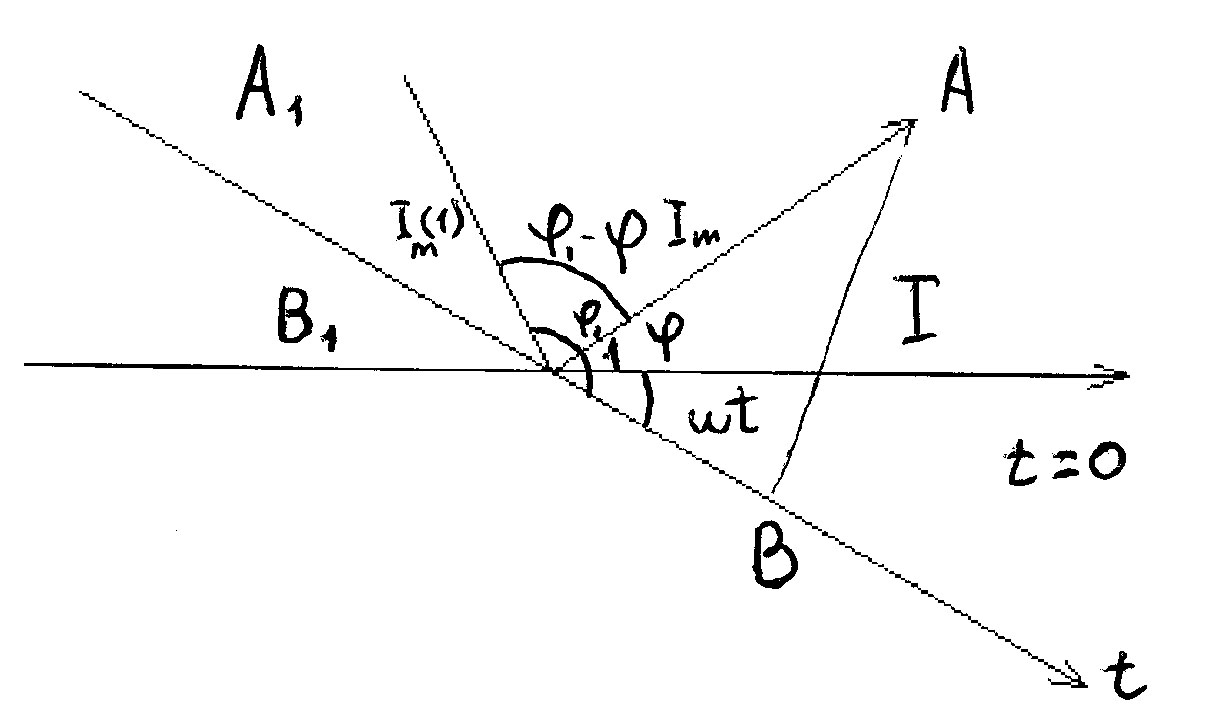
Рис. 13

Під кутом будуємо вектор , модуль якого має довжину . В момент вектор утворює кут з віссю часу , яка повернута на кут відносно осі часу Проекція вектора на напрям, перпендикулярний осі часу , це величина .

Іншу величину дістанемо, відклавши від осі часу кут , або від кут . На промені відкладаємо величину . Дістанемо точку . Проекція вектора на напрям, перпендикулярний осі часу , це величина (рис. 13).

Аналогічно формулі (40) визначимо напругу, яка також є синусоїдальною. Нехай частота напруги є , фаза — , амплітуда коливань — Тоді напруга

. (41)

Нехай сила струму — вектор . Помножимо його на комплексне число : . Довжина цього вектора зміниться на , а вектор повернеться на кут . Запишемо комплексне число в алгебраїчній формі . Тоді , де — вектор, напрямлений по вектору , а — вектор перпендикулярний вектору

Будь-який вектор можна розкласти по векторах та , тобто

.

При цьому модуль числа дорівнює відношенню довжин векторів та , а аргумент числа — це кут, утворений вектором з вектором .

12.2. Електричний ланцюг змінного струму

Нехай в ланцюг змінного струму включені послідовно опір , самоіндукція і ємність C. Нехай явища стаціонарні і напруга та сила струму є синусоїдальними величинами одного і того ж періоду.

1. Напруга задовольняє співвідношення

(42)

Знайдемо та , використовуючи формулу (40). Дістаємо

.

Таким чином, швидкість зміни сили струму (похідна ) відрізняється від сили струму тим, що амплітуда швидкості зміни сили струму домножається на множник , а до фази додається кут . Це означає, що перпендикулярна до , тобто

.

Знайдемо . Для цього використаємо формулу (40). Маємо Звідки

Таким чином, маємо

.

Зауважимо, що символ означає вектор, відповідний величині , а символ — вектор відповідний величині .

Підставимо знайдені величини та у формулу (42). Вона набуває вигляду:

Позначимо через

, а . (43)

Тоді попереднє співвідношення набуває вигляду

(44)

або

. (45)

Формула (44) представляє розклад вектора на дві складові: ватну складову , напрямлену по і безватну складову , напрямлену перпендикулярно до .

Залежність (45) між векторами напруги і сили струму має вигляд звичайного закону Ома з тією різницею, що замість омічного опору рівняння (45) містить комплексний множник

Множник називається позірним опором ланцюга. Якщо врахувати формулу (43), то він має вигляд

. (46)

Звідки випливає, що множник складається із трьох «опорів»: омічного опору R, опору від самоіндукції і опору ємності . Формула (45) набуває вигляду

. (47)

Середнє квадратичне значення синусоїдальної величини визначається як інтеграл по періоду від квадрата цієї величини, тобто формулою

.

Корінь квадратний із називається ефективним або діючим значенням величини :

. (48)

Обчислимо середню потужність струму в ланцюгу, яка визначається як середнє квадратичне по всьому періоду від миттєвої потужності . Нехай — фаза напруги, — фаза сили струму і , . Знаходимо

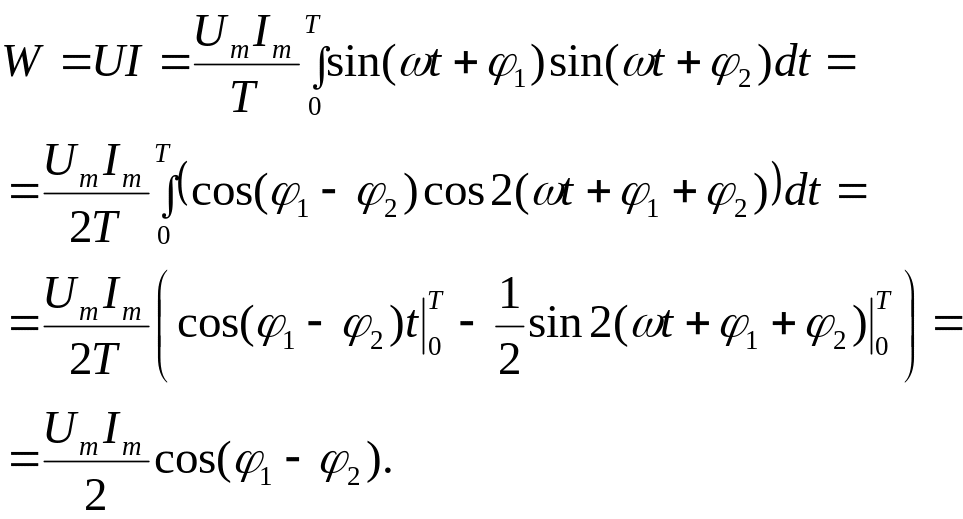
Враховуючи , що і формулу (48), дістаємо

Звідки випливає, що найбільша середня потужність буде, якщо фази напруги і сили струму співпадають або відрізняються на період . В цьому випадку . Найменша потужність буде, якщо фази відрізняються на Тоді .

Безватна складова напруги у формулі (44) дає середню потужність, що дорівнює нулю, тому що вектор перпендикулярний вектору , тобто для нього і вся середня потужність, яка переходить у джоулеву теплоту, визначається ватною («робочою») складовою.

2. Визначимо силу струму.

Із співвідношення (45) знаходимо

(49)

де визначається формулою (43).

Позначимо множник

. (50)

Множник називається позірною провідністю ланцюга і є оберненим до величини позірного опору. Рівняння (49) набуває вигляду

. (51)

Множник називається позірною провідністю ланцюга і є оберненим до величини позірного опору.

Знаходимо

.

Із (51) маємо

Знайдемо . А саме,

. (52)

Тоді, враховуючи формули (50), (52), із (49) маємо формулу для знаходження сили струму

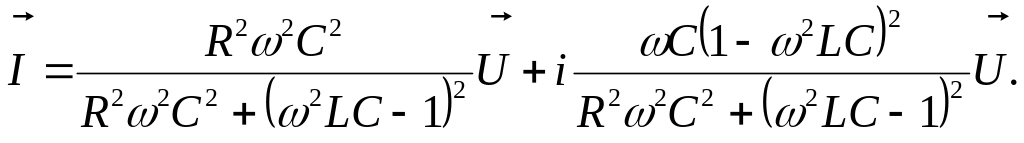(53)

Якщо позначимо множник , то із формули (51) дістанемо

.

2. Паралельне і послідовне включення опорів

Основні правила для обчислення опору складного ланцюга постійного струму залишаються аналогічними і для ланцюгів зі змінним усталеним синусоїдальним струмом, якщо замінити миттєві значення напруги і струму замінити відповідними векторами, а омічні опори – позірними.

Нехай у ланцюг включено послідовно позірні опори

Тоді напруга і сила струму пов’язані співвідношенням

де (54)

При послідовному включенні позірні опори додаються, тобто додаються комплексні числа .

Нехай в ланцюг включено паралельно позірні опори

Тоді

де (55)

Розглянемо паралельне включення двох позірних опорів та Знайдемо комплексне число . Згідно з формулою (55) маємо

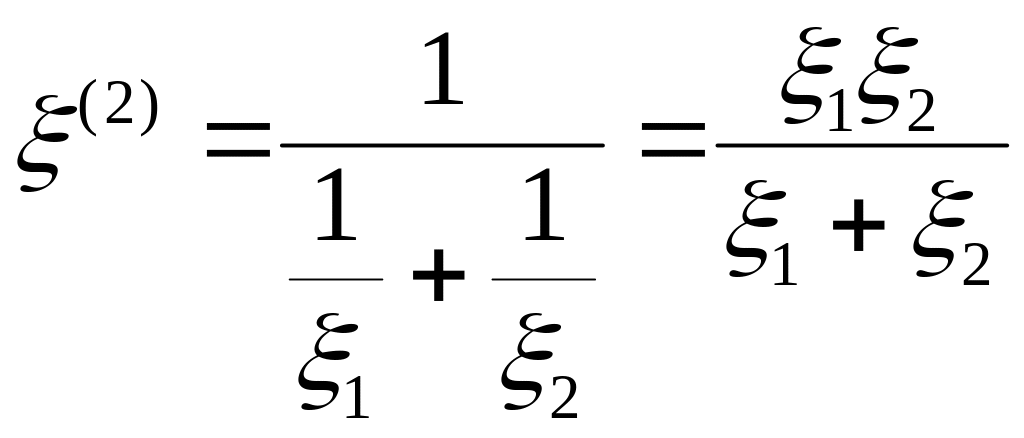. (56)

Задамо позірні опори та комплексними числами в показниковій формі: , .

Нехай шукане комплексне число має вигляд: . Потрібно визначити модуль і аргумент комплексного числа , яке має вигляд (56). Формула (56) містить добуток чисел і та їх суму.

Згідно з означенням добуток комплексних чисел та дорівнює

.

Суму комплексних чисел та можна знайти в алгебраїчній формі, враховуючи, що комплексні числа відповідають векторам. Потім потрібно перейти до показникової форми суми: .

Підставимо значення , , у формулу (56). Дістанемо, що

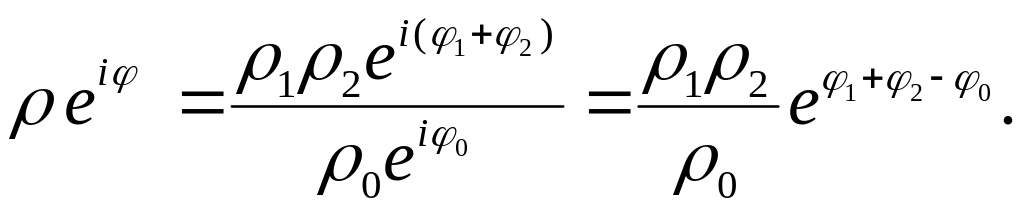
Таким чином, модуль комплексного числа дорівнює ,

а його аргумент дорівнює . Отже. знайдено позірний опір

і тим самим визначена напруга при паралельному включенні двох позірних опорів.