9. Добування кореня із комплексного числа

Коренем степеня із комплексного числа називається комплексне число, –ий степінь якого дорівнює підкореневому виразу.

Нехай . Знайдемо корінь степеня із цього числа:

.

Тоді згідно з означенням ця рівність рівносильна рівності

.

У рівних між собою комплексних чисел рівні між собою модулі , а аргументи відрізняються кутами кратними , тобто . Звідки

,

Позначило корені . Тоді корені степеня мають вигляд:

, (23)

Якщо у формулі (23) покласти то дістанемо , тобто корінь . Таким чином, є значень коренів степеня із комплексного числа .

Запишемо аргумент степеня кореня у вигляді:

, (24)

Формула (23) набуває вигляду

, (25)

Формула (24) містить доданок .

Число (при ) називають поворотним кутом.

При побудові значень коренів доцільно використовувати формулу (24). Геометрично це виглядає так. Для побудови кореня із комплексного числа використовуємо наступне. Обчислюємо значення . Це — аргумент кореня : . Модуль кореня дорівнює .

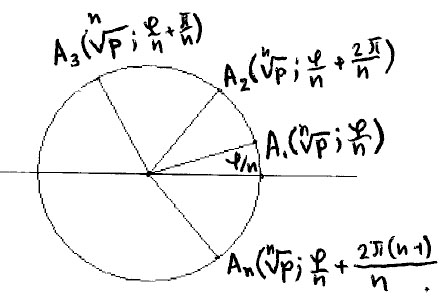
Рис. 10 Рис. 11

Будуємо коло із центром в початку координат і радіусом (рис. 10). Проводимо промінь під кутом . На колі маємо точку , якій відповідає комплексне число .

Якщо промінь , проведений під кутом , повернути на поворотний кут , то при перетині проміня із колом отримаємо точку , якій відповідає другий корінь із комплексного числа . Повертаючи і далі промінь, дістанемо всі інші корені заданого комплексного числа .

Приклад 1. Знайти корені степеня із комплексного числа .

Розв’язання. Знайдемо корені геометрично. Число запишемо в тригонометричній формі. Це від’ємне дійсне число, його аргумент Знаходимо модуль заданого числа: . Задане число в тригонометричній формі має вигляд . Модуль кореня із заданого комплексного числа .

Використаємо формулу (24). Обчислюємо . Знаходимо поворотний кут . Будуємо коло радіуса (рис. 11). Проводимо промінь під кутом . На колі маємо точку . Цій точці відповідає корінь або в алгебраїчній формі . Повертаємо промінь на поворотний кут . Отримуємо точку , симетричну точці відносно уявної осі. Точці відповідає корінь .

В алгебраїчній формі . Повертаємо промінь на поворотний кут . Отримуємо точку , симетричну точці відносно дійсної осі. Точці відповідає корінь

В алгебраїчній формі . Повертаємо промінь на поворотний кут . Отримуємо точку , симетричну точці відносно дійсної осі. Точці відповідає корінь

В алгебраїчній формі .

Таким чином, маємо чотири корені степеня із комплексного числа :

, , , .

Значення коренів — це спряжені комплексні числа: , значення коренів — також спряжені комплексні числа: .

Приклад 2. Знайти корені степеня із комплексного числа .

Розв’язання. Запишемо число в тригонометричній формі. Маємо . Тоді згідно з формулами (10), (11) знаходимо модуль числа : . Аргумент числа :

Таким чином, .

Знайдемо корені степеня із числа . Використаємо формулу (25). Модуль комплексного числа дорівнює . Для того, щоб знайти корені визначаємо Знаходимо поворотний кут . Тоді ,

,

.