6. Ділення комплексних чисел в тригонометричній формі

Результатом ділення комплексних чисел , є комплексне число , модуль якого дорівнює відношенню модулів цих чисел , а аргумент дорівнює різниці аргументів цих чисел: (рис. 9). Тобто,

(18)

Доведемо цю формулу. Для того, щоб розділити комплексне число на число , потрібно ділене і дільник помножити на число , спряжене до дільника, врахувати формулу (15) і виконати дію множення. А саме,

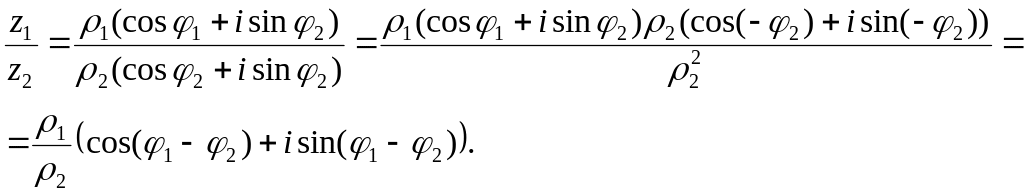
Отже, формула (18) доведена.

Приклад. Знайти , де .

Розв’язання. Запишемо комплексні числа в тригонометричній формі. Для комплексного числа дійсна частина , уявна частина . Тоді, використовуючи формули (10) та (11), знаходимо модуль і аргумент Таким чином, комплексне число в тригонометричній формі набуває вигляду

Для комплексного числа дійсна частина , уявна частина . Тоді, використовуючи формули (10) та (11), знаходимо модуль і аргумент Комплексне число в тригонометричній формі набуває вигляду Використовуючи правило ділення комплексних чисел в тригонометричній формі (формула (18)), знаходимо

Для комплексно спряжених чисел мають місце співвідношення

(19)

Доведемо перше співвідношення із формул (19). Згідно з формулою (14) множення комплексних чисел маємо

.

Комплексне число, спряжене до добутку , має вигляд:

.

З іншої сторони, знаходимо добуток спряжених комплексних чисел та :

Порівнюючи праві частини цього співвідношення і попереднього, бачимо, що вони рівні між собою. Отже рівні і ліві частини цих співвідношень, тобто доведено, що .

Друге співвідношення (19) доведіть самостійно.

7. Множення і ділення комплексних чисел в алгебраїчній формі

7.1. Правило множення. Для того, щоб перемножити два комплексних числа в алгебраїчній формі, потрібно перемножити їх як буквені вирази і врахувати, що . Результат записати у вигляді .

А саме, маємо

Тобто

. (20)

Добуток комплексного числа на спряжене комплексне число дорівнює сумі квадратів дійсної і уявної частини цього числа

. (21)

Доведемо формулу. Дійсно, Тобто, .

Поміняємо місцями ліву і праву частини рівності (21). Тоді

.

Тобто, сума квадратів та дорівнює добутку суми перших степенів числа та комплексного числа на їх різницю:

.

7.2. При діленні комплексних чисел в алгебраїчній формі застосовуємо правило, аналогічне правилу ділення комплексних чисел в тригонометричній формі.

Для того, щоб розділити комплексне число на число , потрібно ділене і дільник помножити на число , спряжене до числа , і далі виконати дію множення і врахувати, що . Тоді

.

Приклад. Знайти , де .

Розв’язання. Маємо . Тоді

.

Для комплексних чисел справедливі ті ж самі закони, що і для дійсних чисел — переставний, розподільчий, сполучний а також існування одиниці і нуля. А саме,

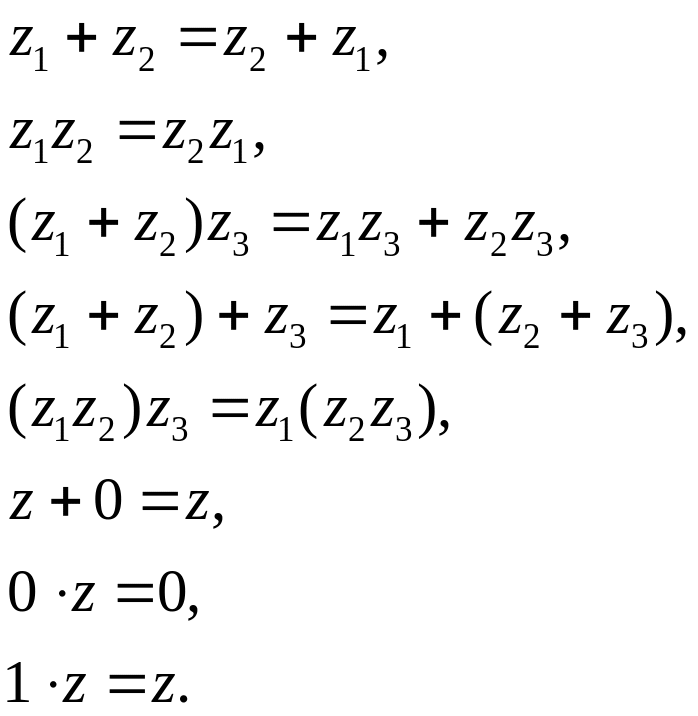
ЛЕКЦІЯ 2.

Степені комплексних чисел. Добування кореня

із комплексного числа. Розклад многочлена на множники

8. Степені комплексних чисел

Знайдемо степінь комплексного числа , тобто .

Спочатку знайдемо . Із означення множення двох комплексних чисел маємо

,

тобто

.

Використовуючи математичну індукцію, дістаємо, що

. (22)

Таким чином, маємо правило піднесення комплексного числа до степеня .

Правило. При піднесенні до степеня комплексного числа його модуль підноситься до степеня , а аргумент множиться на .

Формула (22) називається формулою Муавра.

Приклад 1. Знайти .

Розв’язання. Запишемо число в тригонометричній формі. Маємо . Згідно з формулами (10) та (11) знаходимо модуль числа : . Аргумент . Комплексне число в тригонометричній формі має вигляд . Тоді згідно з формулою (22) дістаємо , тобто в тригонометричній формі

.

а в алгебраїчній формі

.

Приклад 2. Знайти .

Розв’язання. Спочатку запишемо число , спростивши цей вираз, тобто виконаємо дію ділення комплексних чисел в алгебраїчній формі. А саме, домножимо чисельник і знаменник на комплексне число, спряжене до знаменника. Маємо

.

Тоді, враховуючи формули (17), дістаємо