4. Тригонометрична форма комплексного числа

Нехай вектор має координати та в декартовій системі координат. Задамо цей вектор в полярній системі координат, в якій полярна вісь співпадає з віссю , а полюс — з початком координат.

Точка в полярній системі

координат має координати

та , де — кут, що обчислюється

проти годинникової стрілки від

Рис. 6 додатного напряму осі (рис. 6).

Тобто, точка в полярній системі координат має координати .

Між полярними координатами і точками комплексної площини не буде взаємно однозначної відповідності, оскільки точку визначають і координати . Тому що, повертаючи промінь на , ми знову потрапимо в його попереднє положення.

Розглянемо зв’язок між координатами точки в декартовій системi координат: і в полярній системi координат: . Із рис. 6 маємо

, (9)

. (10)

Звідки і .

Кут називається аргументом комплексного числа : , а — його модулем: .

Розглядатимемо надалі основне значення аргументy: . А саме,

(11)

Якщо — дійсне додатне число, то або

Якщо — дійсне від’ємне число, то .

Якщо — суто уявне число і , то

Якщо — суто уявне число і , то .

Якщо то не має сенсу.

Підставимо у формулу (5) значення та із формул (9). Дістанемо

.

Маємо

тригонометричну форму комплексного числа

, (12)

де — аргумент комплексного числа , — його модуль.

Зауваження. Тригонометрична форма комплексного числа — це вираз (12), у якому між дійсною і уявною частинами комплексного числа завжди має стояти знак .

Приклад. Зобразити комплексне число на площині.

Розв’язання. Запишемо задане число у тригонометричній формі: Отже, модуль заданого комплексного числа , аргумент .

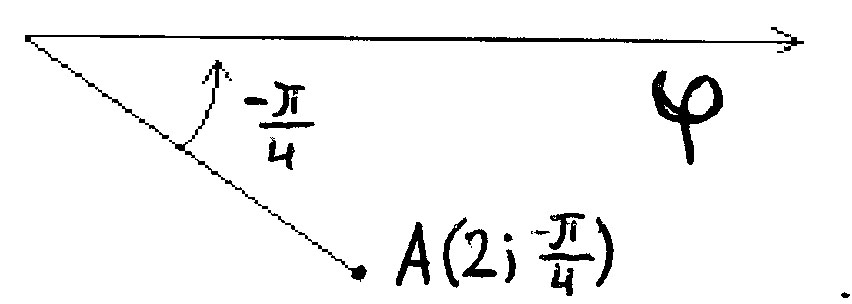
Під кутом із початку координат

проводимо промінь і відкладаємо на

ньому відрізок (рис. 7).

Дістаємо точку , якій відповідає Рис. 7

задане число .

Наведемо запис дійсних чисeл , та суто уявних чисeл , в тригонометричній формі. A саме, вони мають вигляд:

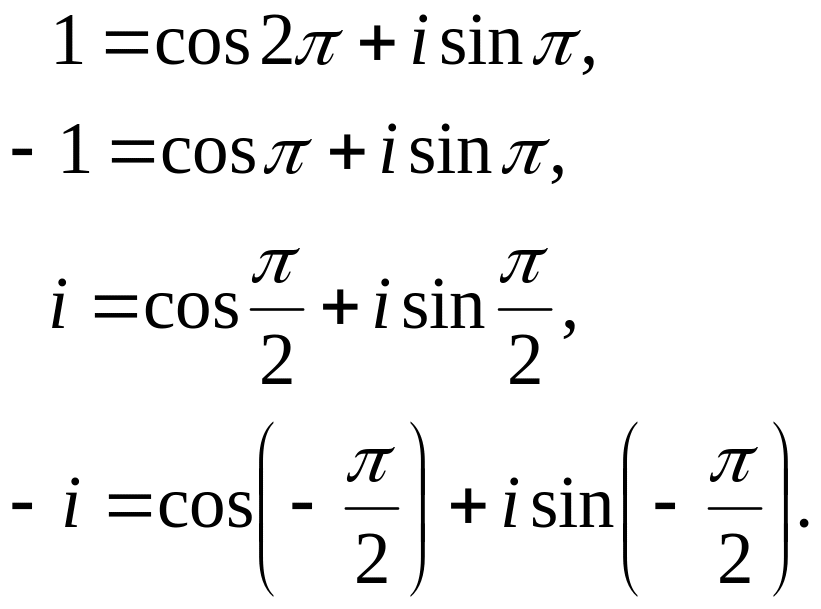(13)

Комплексне число , спряжене до числа , має модуль, який співпадає з модулем числа : і аргумент, протилежний аргументу числа : , тобто

.

Kомплексне число , cпряжене числу , розташоване симетрично йому відносно полярної осі.

5. Множення комплексних чисел в тригонометричній формі

Означення. Добутком двох комплексних чисел , називається комплексне число, модуль якого дорівнює добутку модулів співмножників, а аргумент — сумі аргументів співмножників, тобто має місце формула

. (14)

Множення двох комплексних чисел та показано на рис. 8, де ,

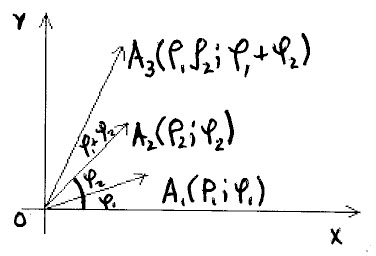
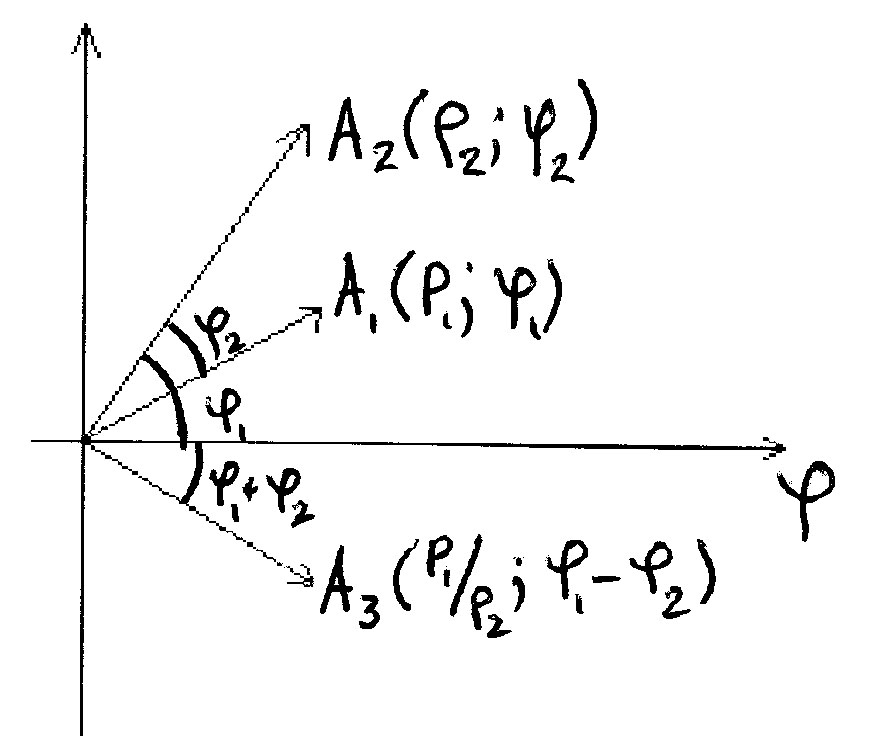
Рис. 8 Рис. 9

За вказаним правилом можна множити будь-яку скінчену кількість комплексних чисел.

При множенні комплексних чисел у тригонометричній формі їх модулі перемножаються, а аргументи додаються:

.

5.1.1. Добуток комплексного числа на спряжене дорівнює квадрату модуля:

. (15)

Доведемо цю формулу. Використовуючи правило множення комплексних чисел (14), маємо

Отже, формула (15) доведена.

5.1.2. Kомплексне число та його властивості

Запишемо комплексне число у тригонометричній формі, використовуючи формулу (13). Маємо . Знайдемо добутoк комплексного числа на :

.

Отже,

.

Звідки

. (16)

Це пояснює, чому комплексне число називають уявною одиницею — квадрат цього числа є від’ємне число , а для дійсних чисел квадрат будь-якого дійсного числа — це додатне число.

Cтепені числа

Знайдемо степені числа . Маємо:

.

Отже, для будь-якого додатного числа дістаємо:

. (17)

Приклад. Записати в алгебраїчній формі комплексне число

. Знайти .

Розв’язання. Використовуючи формули (17), маємо

.

Отже,