2. Рівність двох комплексних чисел

Комплексні числа та рівні між собою, якщо рівні між собою окремо їх дійсні частини і уявні частини:

. (3)

Це випливає із рівності двох векторів: два вектори рівні між собою, якщо рівні між собою відповідні проекції векторів.

Зокрема, комплексне число дорівнює нулю, якщо рівні нулю його дійсна і уявна частини: і навпаки, якщо рівні нулю дійсна і уявна частини комплексного числа, то комплексне число дорівнює нулю:

.

3. Додавання і віднімання комплексних чисел в алгебраїчній формі

Розглянемо два комплексні числа та . Їм відповідають вектори та .

Сумою двох векторів є вектор , що з’єднує початок першого вектора з кінцем другого вектора , якщо другий вектор бере свій початок в кінці першого вектора (рис. 3).

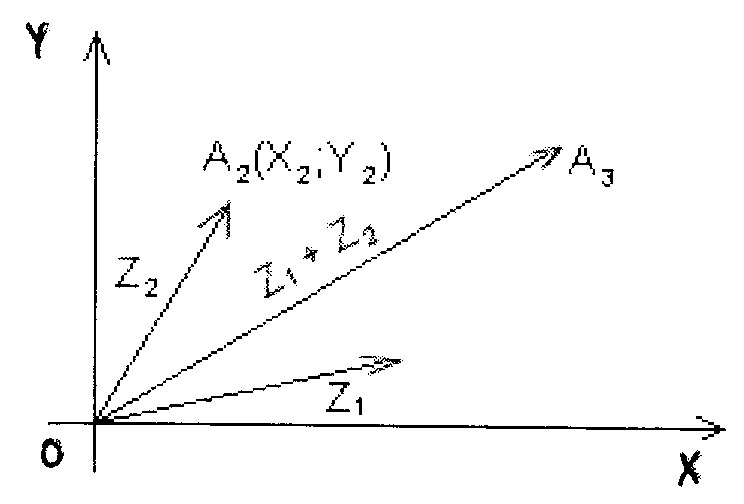
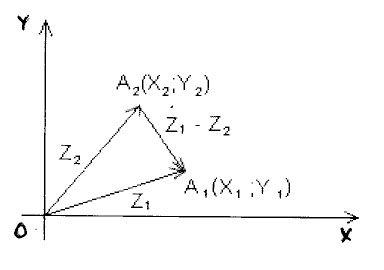
Рис. 3 Рис. 4

Проекції вектора суми векторів на координатні осі дорівнюють сумі відповідних проекцій цих векторів, тобто

.

Вектору суми векторів та відповідає комплексне число — сума комплексних чисел та . Отже,

. (4)

Формула, аналогічна формулі (4), має місце і при додаванні будь-якої скінченої кількості комплексних чисел:

.

При додаванні комплексних чисел в алгебраїчній формі окремо додаються дійсні частини комплексних чисел і окремо уявні частини.

Повернемося до запису комплексного числа. Тепер комплексне число можна записати як суму двох комплексних чисел — дійсного числа і суто уявного числа :

.

Отже, комплексне число — це сума дійсного числа і суто уявного числа . Знак у записі надалі розглядається як знак додавання.

Таким чином, маємо алгебраїчну форму комплексного числа

, (5)

де . При цьому в алгебраїчній формі комплексного числа (5) завжди має стояти знак .

Приклад. Нехай . Тут і алгебраїчна форма цього числа має вигляд:

Дію віднімання двох комплексних чисел розглядаємо як дію, обернену до дії додавання.

Нехай та (рис. 4). Знайдемо

, де .

Тоді . Згідно з означенням дії додавання маємо

.

Два комплексні числа рівні між собою, якщо рівні між собою дійсна і уявна частини цих чисел, тобто . Звідки . Отже, різницю комплексних чисел знаходимо за формулою

. (6)

3.1. Cпряженi комплекснi числа

Комплексне число називається спряженим до комплексного числа , якщо в алгебраїчній формі комплексного числа замінити на , тобто

або . (7)

Задане комплексне число і спряжене

до нього розташовані симетрично

відносно осі (рис. 5).

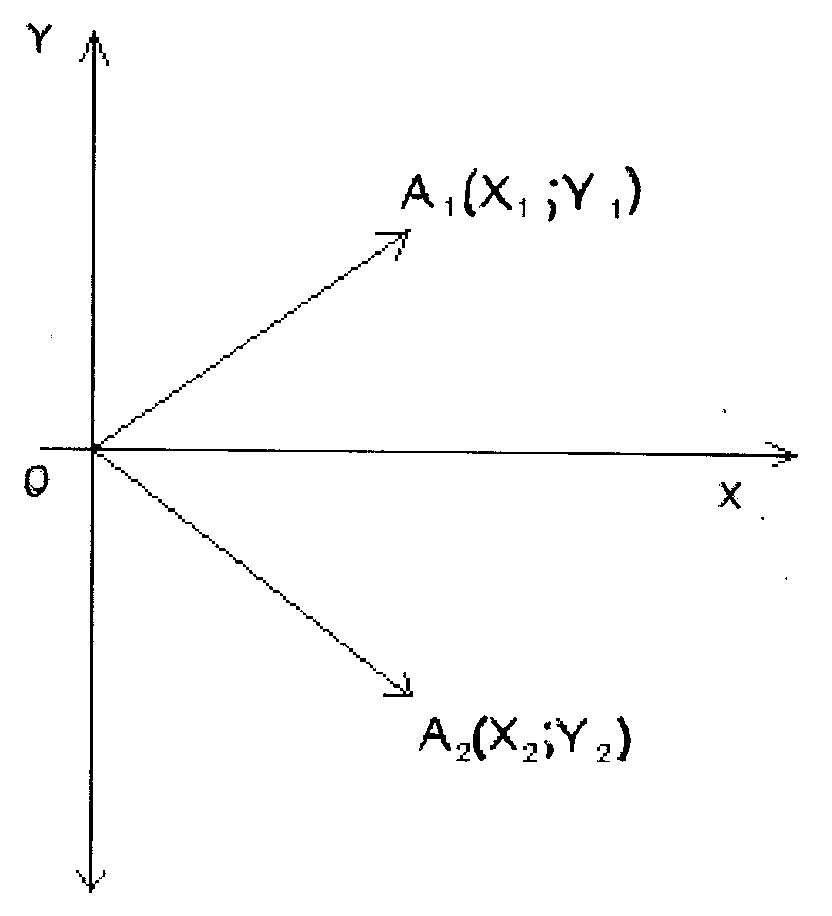
Так, спряженими до чисел

Рис. 5 будуть числа .

3.1.1. Властивості спряжених комплексних чисел

Для спряжених комплексних чисел справедливе твердження:

1. Комплексне число, спряжене до суми комплексних чисел, дорівнює сумі спряжених чисел:

. (8)

Доведення. Cума комплексних чисел та дорівнює

.

Спряжене комплексне число до цієї суми має вигляд

.

З іншої сторони, cума спряжених комплексних чисел дорівнює

.

Порівнюючи останні рівності, бачимо, що твердження (8) справджується.

Приклад. Знайти спряжене число до суми чисел

Розв’язання. Знаходимо суму заданих чисел за формулою (4):

. Згідно з означенням спряженого комплексного числа дістаємо, що .

3.1.2. Мають місце також наступні твердження, які легко перевірити. А саме,

• сума комплексного числа і спряженого до нього є дійсне число .

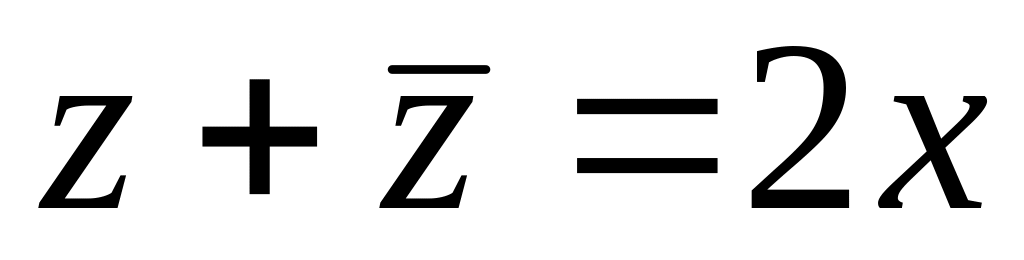• різниця комплексного числа і спряженого до нього є суто уявне число .

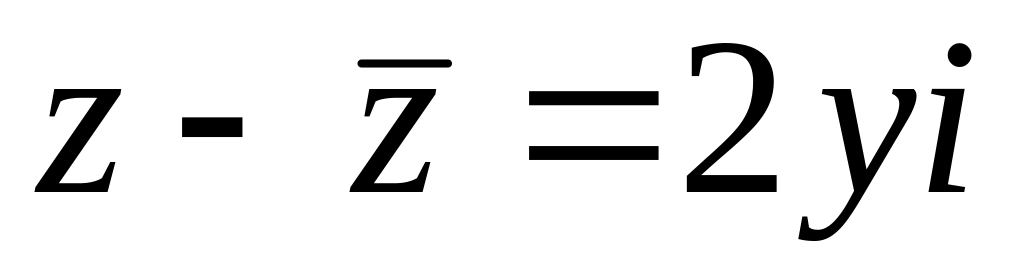Доведення. Маємо

, , тобто дійсно твердження мають місце