Взаимосвязь между двумя количественными признаками

Используют коэффициент корреляции Пирсона, рассчитываемый по следующей формуле:

Этот коэффициент изменяется от -1 до +1:

если коэффициент равен ± 1 – между признаками существует функциональная связь

±0,81 до ± 1 – сильная связь

±0,61 до ± 0,80 - умеренная связь

±0,41 до ± 0,60 – слабая связь

±0,21 до ± 0,40 – очень слабая связь

от 0 до ± 0,20 – связь между признаками отсутствует

В зависимости от объема выборочной совокупности предлагается различные методы оценки существенности коэффициента корреляции:

1. При большом объеме выборки, отобранной из нормально распределенной совокупности, средняя ошибка коэффициента корреляции равна:

2. Для малого объема выборочной совокупности используется критерий Стьюдента:

Если величина коэффициента корреляции больше среднеквадратической ошибки более чем в t_ασ_r раз, то можно говорить о существенности выборочного коэффициента корреляции.

Доверительный интервал для коэффициента корреляции равен:

Теперь необходимо исследовать форму связи. Как правило, корреляционный анализ дополняется регрессионным анализом, то есть мы должны построить уравнение регрессии.

Тип модели выбирается на основе сочетания теоретического анализа и исследования эмпирических данных посредством построения эмпирической линии регрессии.

Чаще всего используются следующие типы функций:

а) линейная функция:

б) гиперболическая функция:

в) параболическая функция:

г) показательная функция:

Система нормальных уравнений для определения параметров а и в уравнения линейной корреляции связи выводится методом наименьших квадратов, и изобразить ее можно следующим образом:

, где S_x² – дисперсия переменной х

Если существует зависимая переменная z и 2 факторные переменные, то линейное уравнение регрессии имеет следующий вид:

Тогда система нормальных уравнений для вычисления параметров а, в и с будет выглядеть следующим образом:

В этом случае можно рассчитать 3 парных коэффициента корреляции:

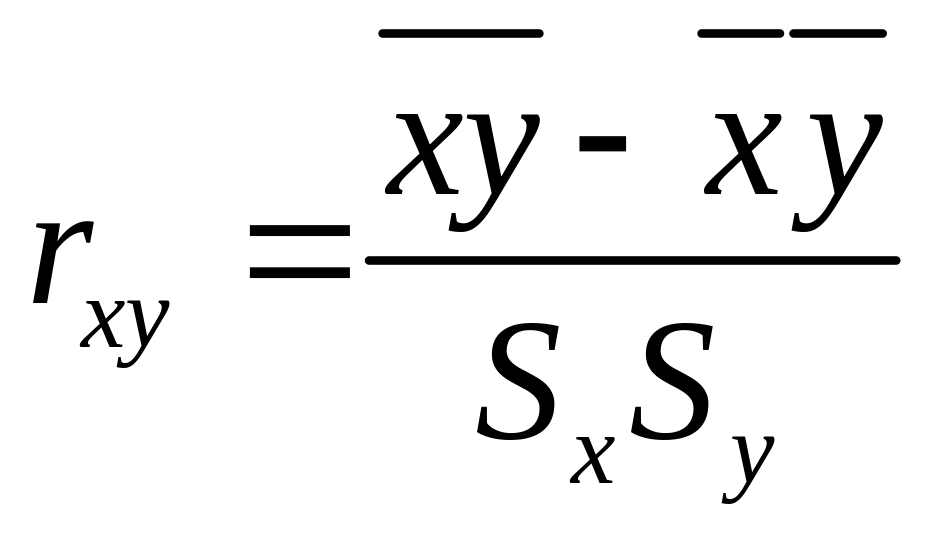
где S_x, S_y, S_z – среднеквадратические отклонения соответственно по х, у и z, рассчитываемые по следующим формулам:

Чтобы построить уравнение регрессии, после вычисления парных коэффициентов корреляции нужно вычислить параметры а, в и с:

Для измерения степени тесноты связи между изменениями результативного признака z и изменениями значений факторных признаков х и у определяют совокупный коэффициент корреляции R:

Данный коэффициент имеет следующие свойства:

1. Совокупный коэффициент корреляции изменяется в пределах от 0 до 1.

2. если он равен 0, то линейной связи между величинами х, у и z не существует, то есть между переменными может существовать и нелинейная корреляция

3. если данный коэффициент равен 1, то между величинами х, у и z существует функциональная взаимосвязь.

Кроме совокупного коэффициента корреляции существуют частные коэффициенты корреляции, которые показывают влияние отдельных факторов на исследуемую величину. Таких частных коэффициентов существует 2:

1)

Этот коэффициент служит мерой тесноты линейной связи между х и z при постоянном у.

2)

Этот коэффициент показывает тесноту связи между у и z при постоянном х.

Свойства частных коэффициентов корреляции такие же, как и свойства коэффициента линейной корреляции:

1. изменяются в пределах от -1 до +1

2. отрицательное значение говорит о том, что связь обратная, а положительное – что связь прямая.

Каждый из частных коэффициентов корреляции по своей абсолютной величине не может быть больше величины совокупного коэффициента корреляции.

Влияние отдельных факторов в многофакторных моделях может быть охарактеризовано с помощью частных коэффициентов эластичности, которые в случае линейной двухфакторной модели рассчитываются по следующим формулам:

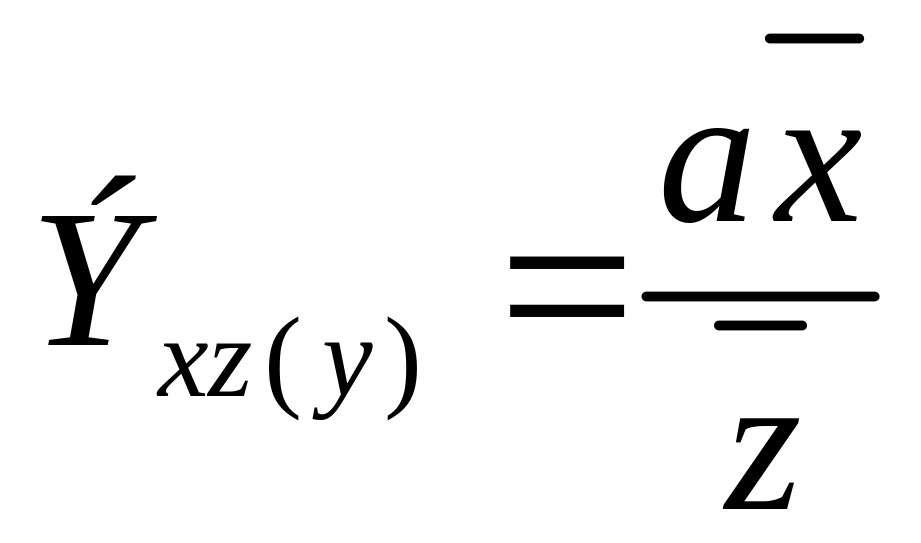
Частные коэффициенты эластичности показывают, на сколько процентов изменится результативный признак, если значение одного из факторных признаков изменится на 1%, а значение другого факторного признака останется неизменным.

Существуют также частные β – коэффициенты, рассчитываемые по следующим формулам:

Они показывают, на какую долю своего среднеквадратического отклонения изменится в среднем результативный признак при изменении одного из факторных признаков на величину его среднеквадратического отклонения и неизменном значении остальных факторов.

Частные коэффициенты детерминации – это возведенные в квадрат частные коэффициенты корреляции. Они показывают долю вариации результативного признака под действием одного из факторных признаков при неизменном значении другого фактора.