2.7. Эффекты Холла, Зеебека и Пельтье

Эффект Холла основан на взаимодействии между движущимися носителями электрического заряда и внешним магнитным полем. В металлах носителями за­рядов являются электроны. При движении электронов в магнитном поле на них действует отклоняющая сила:

F=qvB (2.7.1)

где q = 1,6*10^-19Кл — величина заряда элект­рона, v — его скорость, а В — магнитная ин­дукция. Выделенный шрифт указывает на то, что F и В являются векторами. Направление силы и ее величина зависят от пространствен­ного расположения магнитного потока и на­правления движения электрона. Единицей измерения В является тесла: 1 Тесла = 1 Ньютон/(амперхметр)= 10⁴Гаусс.

Рис.2.7.1. Датчик Холла. Магнитное поле отклоняет движущийся электрический заряд.

Предположим, что электроны двигаются внутри электропроводной пластины, помещен­ной в магнитное поле В (рис.2.7.1). На две сто­роны пластины нанесены дополнительные электроды, подключенные к вольтметру. Еще два электрода расположены сверху и снизу пластины, они подсоединены к источнику электричес­кого тока. Из-за действия внешнего магнитно­го поля возникает отклоняющая сила, смещаю­щая электроны ближе к правому краю пласти­ны, поэтому эта сторона становится более от­рицательно заряженной, чем левая. Очевидно, что вследствие взаимодействия магнитного поля и электрического тока возникает поперечная раз­ность потенциалов, получившая название напря­жение Холла. Знак и амплитуда этого напря­жения зависят как от величины, так и направления магнитного и электрического по­лей. При фиксированной температуре оно определяется выражением:

(2.7.2)

где α — угол между вектором магнитного поля и плоскостью пластины Холла (рис.2.7.2), a h — полная чувствительность датчика, на значение которой влияют тип материала пластины, ее геометрия (площадь активной зоны) и температура.

Полная чувствительность датчика Холла зависит от коэффициента Холла, ко­торый определяется градиентом поперечного электрического потенциала на еди­ницу интенсивности магнитного поля и на единицу плотности тока. В соответ­ствии с теорией свободных электронов в металлах, коэффициент Холла можно найти при помощи выражения:

(2.7.3)

где N — число свободных электронов в единице объема, а с — скорость света. В зависимости от кристаллической структуры материала заряды могут быть либо электронами (отрицательными), либо дырками (положительными). Поэтому и эффект Холла бывает либо положительным, либо отрицательным.

Рис.2.7.2. А – выходной сигнал датчика Холла зависит от угла между вектором магнитного поля и плоскостью пластины; Б – четыре вывода датчика Холла.

В 1821 году физик Т. Зеебек (1770-1831), родившийся в Эстонии, а учившийся в Германии, изучая тепловые эффекты в гальванических устройствах, соединил полукруглые элементы, изготовленные из висмута и меди. Неожиданно стрел­ка компаса, случайно лежавшего рядом, отклонилась (рис.2.7.3А). Он проверил этот эффект на других соединениях металлов при разных температурах и обнару­жил, что каждый раз получается различная напряженность магнитного поля. Од­нако, Зеебек не догадался, что при этом через элементы течет электрический ток, поэтому назвал это явление термомагнетизмом.

Если взять проводник, и один его конец поместить в холодное место, а дру­гой — в теплое, от теплого участка к холодному будет передаваться тепловая энер­гия. Интенсивность теплового потока при этом пропорциональна теплопровод­ности проводника. В дополнение к этому градиент температур приводит к появ­лению в проводнике электрического поля, обусловлено эффектом Томсона (В. Томпсон открыл этот эффект приблизительно в 1850 году. Он заключается в по­глощении или высвобождении тепла линейно пропорционально току, проходя­щего через однородный проводник, имеющий градиент температуры вдоль его длины. При этом тепло поглощается, если ток и тепловой поток направлены в противоположных направлениях, и выделяется — когда они имеют одинаковое направление). Индуцированное электрическое поле приводит к появлению раз­ности потенциалов:

(2.7.4)

где dT — градиент температуры на небольшом участке длины dx, а α_α — абсолют­ный коэффициент Зеебека материала. Если материал однородный, α_α не зави­сит от его длины, и уравнение принимает вид:

(2.7.5)

Уравнение (2.7.5) является основным математическим выражением для термоэлек­трического эффекта. На рис.2.7.3Б показан проводник с неравномерным распределением температуры Т вдоль его длины х. Градиент температуры между произ­вольно расположенными точками определяет термоэ.д.с между ними. Другие зна­чения температур (например, Т₃, Т₄ и Т₅) не влияют на значение э.д.с. между точ­ками 1 и 2. Для измерения э.д.с. вольтметр подсоединяется к проводнику, как по­казано на рис.2.7.4Б. Это не так просто, как может показаться на первый взгляд. Для измерения термо э.д.с. надо соответствующим образом подключить щупы вольтметра. В таком контуре измеритель включается последова­тельно с проводником. Если контур выполнен из одинакового материала, то тока в цепи не будет, даже при неравномерной температуре вдоль его длины. Посколь­ку в этом случае две половины контура создадут токи равной величины, но про­тивоположного направления, которые взаимно уничтожат друг друга. Термо э.д.с. возникает в любом проводнике с неравномерной температурой, но ее часто не­возможно измерить напрямую.

Для исследования термоэлектричества необходимо иметь контур, составленный из двух разных материалов (или из одинаковых материалов, но находящихся при раз­личных условиях, например, один — в напряженном состоянии, а другой нет).

Только тогда возможно определить разницу их термоэлектрических свойств. На рис.2.7.4Б показан контур, состоящий из двух различных металлов, в котором возникает разность токов: Δi = i_a— i_b. Величина Δi зависит от многих факторов, включая форму и размер проводников. Если вместо тока измерять напряжение на разомкнутом проводнике, разность потенциалов будет определяться только ти­пом материалов и их температурой и не будет зависеть ни от каких других факто­ров. Индуцированная теплом разность потенциалов называется напряжением Зеебека.

Что происходит, когда два проводника соединяются друг с другом? Свободные электроны в металле ведут себя как идеальный газ. Кинетическая энергия электро­нов определяется температурой материала. Однако в разных металлах энергия и плот­ность свободных электронов не являются одинаковыми.

Рис.2.7.3.А – опыт Зеебека; Б – переменная температура вдоль проводника является причиной возникновения термо ЭДС.

Рис.2.7.4. Термоэлектрический контур: А – соединение идентичных металлов не приводит к появлению тока при любой разности температур; Б – соединение разных металлов индуцирует ток Δi.

Когда два разных материа­ла, находящихся при равной температуре, соприкасаются друг с другом, свободные электроны за счет диффузии перемещаются через место соединения. Электри­ческий потенциал материала, принявшего электроны, становится более отрицатель­ным, а материал, отдавший электроны, — более положительным. Разные концентра­ции электронов с двух сторон соединения формируют электрическое поле, уравно­вешивающее процесс диффузии, в результате чего устанавливается некоторое равно­весие. Если контур является замкнутым, и оба соединения находятся при одинако­вой температуре, электрические поля около них взаимно уничтожаются, чего не про­исходит, когда места соединений имеют разную температуру.

Последующие исследования показали, что эффект Зеебека является элек­трическим по своей природе. Можно утверждать, что термоэлектрические свой­ства проводников — это такие же объемные свойства материалов, как электро- и теплопроводность, а коэффициент α_α — уникальная характеристика материала. При комбинировании двух разных материалов (А и В) всегда требуется опреде­лять напряжение Зеебека. Это можно сделать при помощи дифференциального ко­эффициента Зеебека:

(2.7.6)

Тогда напряжение на соединении равно:

(2.7.7)

Уравнение (2.7.7) иногда применяется для определения дифференциального коэффициента:

(2.7.8)

Например, функцию напряжения от градиента температуры для термопары Т-типа можно с достаточной степенью точности аппроксимировать при помощи уравнения второго порядка:

(2.7.9)

Тогда выражение для дифференциального коэффициента Зеебека принимает сле­дующий вид:

(2.7.10)

Из уравнения (2.7.10) видно, что коэффициент является линейной функцией от темпера­туры. Иногда он называется чувствительностью термопарного соединения. Эта­лонное соединение, которое, как правило, находится при более холодной темпе­ратуре, называется холодным спаем, а второе соединение — горячим спаем. Коэф­фициент Зеебека не зависит от физической природы соединения: металлы могут быть скручены, сварены, спаяны и т.д. Имеет значение только температура спаев и свойства металлов. Эффект Зеебека является прямым преобразованием тепло­вой энергии в электрическую.

Рис.2.7.5. Эффект Пельтье.

Эффект Зеебека связан с температурной зависимостью энергии Ферми Е_F, поэтому коэффициент Зеебека для кремния n-типа можно аппроксимировать функцией от электричес­кого удельного сопротивления в интересующем температурном диапазоне (для датчиков при комнатной температуре):

(2.7.11)

где ρ₀=5*10^-6 Ом*м и m~2,5 являются константами, к — постоянная Больцмана, a q — электрический заряд. При помощи легирующих добавок получают материалы с коэффициентами Зеебека порядка 0,3...0,6 мВ/К. Коэффициенты Зеебека для металлов гораздо мень­ше, чем для кремния, и что влияние алюминиевых выводов на микросхемы не­значительное из-за высокого значения коэффициента Зеебека для кремния.

В начале девятнадцатого века французский часовщик, в последствии став­ший физиком, Жан Шарль Атанас Пельтье (1785-1845) обнаружил, что при про­хождении электрического тока из одного материала в другой, в месте их соедине­ния происходит либо выделение, либо поглощение тепла, что зависит от на­правления тока:

(2.7.12)

где i — сила тока, dt — время. Коэффициент р имеет размерность напряжения и определяется термоэлектрическими свойствами материала. Следует отметить, что количество тепла не зависит от температуры других соединений.

Эффект Пельтье (рис.2.7.5)— это выделение или поглощение тепла при прохождении электрического тока через соединение двух различных металлов. Это явление ха­рактерно и для случаев, когда ток поступает от внешних источников, и когда он индуцируется в спае термопары из-за эффекта Зеебека.

Эффект Пельтье используется в двух ситуациях: когда надо либо подвести тепло к месту соединения материалов, либо отвести его, что осуществляется изменением на­правления тока. Это свойство нашло свое применение в устройствах, где требуется осу­ществлять прецизионный контроль за температурой. Считается, что эффекты Пель­тье и Зеебека имеют одинаковую природу. Однако следует хорошо понимать, что тепло Пельтье и Джоуля отличаются друг от друга. Тепло Пельтье в отличие от джоулева тепла линейно зависит от силы тока. (Тепло Джоуля выделяется при прохождении электри­ческого тока любого направления через проводник, имеющий конечное сопротивле­ние. Высвобождаемая при этом тепловая энергия пропорциональна квадрату тока: Р= i²/R, где R — сопротивление проводника). Величина и направленность тепловой энер­гии Пельтье не зависит от физической природы соединения двух различных материа­лов, а полностью определяется их объемными термоэлектрическими свойствами. Эф­фект Пельтье используется для построения термоэлектрических охладителей, приме­няемых для снижения температуры детекторов фотонов, работающих в дальнем ИК диапазоне спектра, а также охлаждаемых зеркальных гигромет­ров.

Необходимо помнить, что в любом месте схемы, где соединяются два или бо­лее различных металла, имеющих разную температуру, всегда возникает термо­электрический ток. Эта разность температур всегда сопровождается явлением теп­лопроводности Фурье, а при прохождении электрического тока выделяется тепло Джоуля. В то же самое время протекание электрического тока всегда связано с эффектом Пельтье: выделением или поглощением тепла в местах соединения раз­личных металлов, при этом разность температур также вызывает появление эф­фекта Томпсона: нагрев или охлаждение проводников вдоль их длины. Эти два тепловых эффекта (Томпсона и Пельтье) выражаются в виде четырех составляю­щих в выражении для э.д.с. Зеебека:

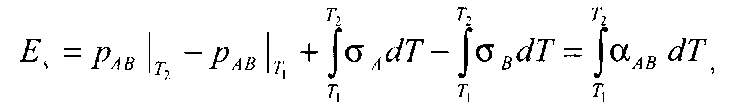(2.7.13)

где σ — величина, называемая коэффициентом Томпсона, которую сам Томсон называл удельной теплоемкостью электричества, проводя аналогию между α и обычной удельной теплоемкостью с, принятой в термодинамике. Величина σ по­казывает с какой скоростью происходит выделение или высвобождение тепла на единицу разности температур и на единицу массы.