2.4. Индукция

Закон Фарадея о магнитной индукции гласит, что индуцированное напряжение или элек­тродвижущая сила (э.д.с.) в контуре численно равна и противоположна по знаку скорости изменения магнитного потока Фв, сквозь поверхность ограниченную этим контуром, т.е.

(2.4.1)

Поскольку скорость изменения потока выражается в вебер/секунду, э.д.с. изме­ряется в вольтах. Знак минус показывает направление индуцированной э.д.с. При прохождении через соленоид переменного магнитного потока, полная э.д.с. по­лучается из суммы э.д.с, индуцируемых в каждом витке. Если все витки соленои­да имеют одинаковую площадь поперечного сечения, через них будут проходить равные магнитные потоки, тогда индуцированное напряжение можно найти по следующей формуле:

(2.4.2)

где N — число витков. Это уравнение можно переписать в виде:

(2.4.3)

Это выражение имеет большее практическое применение при разработке датчи­ков. Оно означает, что навести напряжение в контуре можно, изменяя либо маг­нитную индукцию (В), либо площадь контура (А). Величина этого напряжения зависит от следующих факторов:

• движения источника магнитного поля (магнита, катушки, провода и т.д.);

• изменения тока в катушке или проводе, индуцирующего магнитное поле;

• изменения ориентации источника магнитного поля по отношению к контуру;

• изменения геометрии контура (например, его растяжения или сжатия, или изменения в нем числа витков).

Если электрический ток протекает через катушку, находящуюся в непосред­ственной близости от другой катушки, из закона Фарадея следует, что во второй катушке будет также индуцирована э.д.с. Однако магнитный поток проникнет не только во вторую катушку, но и в первую. Это означает, что в первой катушке магнитное поле также наведет э.д.с. Это явление называется самоиндукцией, а ре­зультирующее напряжение — э.д.с. самоиндукции. Закон Фарадея для центральной части соленоида можно записать как:

(2.4.4)

Значение в круглых скобках называется потокосцеплением и является очень важ­ной характеристикой устройства. Для простой катушки, в окрестности которой нет никаких магнитных материалов, эта величина пропорциональна току, проте­кающему через нее:

(2.4.5)

где L — коэффициент пропорциональности, называемый индуктивностью катуш­ки. Тогда уравнение (2.4.4) можно переписать в виде:

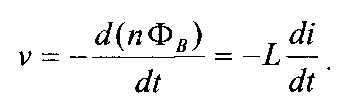(2.4.6)

Из этого уравнения получаем выражение для индуктивности:

(2.4.7)

Таким образом, если в окрестности индуктора (устройства, обладающего индуктив­ностью) нет никаких магнитных материалов, его индуктивность определяется урав­нением (2.4.7) и зависит только от геометрии устройства. В системе СИ индуктив­ность измеряется в (Вольт*секунда)/Ампер. Эта единица названа в честь американс­кого физика Джозефа Генри (1797-1878): 1 Генри = 1 Вольт*секунду/Ампер и обозна­чается Гн.

Из уравнения (2.4.6) можно сделать несколько выводов:

• индуцированное напряжение пропорционально скорости изменения тока через индуктор;

• в случае постоянного тока индуцированное напряжение равно нулю;

• индуцированное напряжение линейно связано со скоростью изменения тока;

• полярность индуцированного напряжения будет разной при увеличении и уменьшении скорости тока, текущего в одном и том же направлении;

• индуцированное напряжение всегда противостоит изменению тока.

Также как и в случае емкости на величину индуктивности влияют геометри­ческие факторы. Для катушки с плотно намотанными витками справедливо:

(2.4.8)

Если n — число витков на единицу длины, потокосцепление в катушке длиной l можно определить по формуле:

(2.4.9)

где А — поперечное сечение катушки. Для соленоида В=μ₀ni, а индуктивность:

(2.4.10)

Следует отметить, что lА — объем соленоида. Таким образом, индуктивность мож­но менять, изменяя только геометрию катушки, оставив количество витков неиз­менным.

При расчете электронной схемы индуктивность иногда представляют в виде комплексного сопротивления:

(2.4.11)

Из выражения (2.4.11) видно, что комплексное сопротивление индуктора увеличивается с ростом часто­ты. Уравнение называется законом Ома для индукторов. Из него видно, что ток отстает от напряжения на 90°.

Если две катушки находятся в непосредственной близости друг от друга, одна из катушек наводит э.д.с. υ₂ во второй катушке:

(2.4.12)

где М₂₁ — коэффициент взаимной индуктивности двух катушек. Вычисление вза­имной индуктивности является очень непростой задачей, поэтому на практике ее часто определяют экспериментально. Однако для самых простых случаев суще­ствуют формулы для ее расчета. Например, для катушки из N витков, размещен­ной вокруг длинного соленоида (рис.2.4.1А), имеющего n витков на единицу дли­ны, выражение для взаимной индуктивности имеет вид:

(2.4.13)

А для катушки, намотанной на тороид (рис.2.4.1Б), взаимную индуктивность мож­но найти по формуле:

(2.4.14)

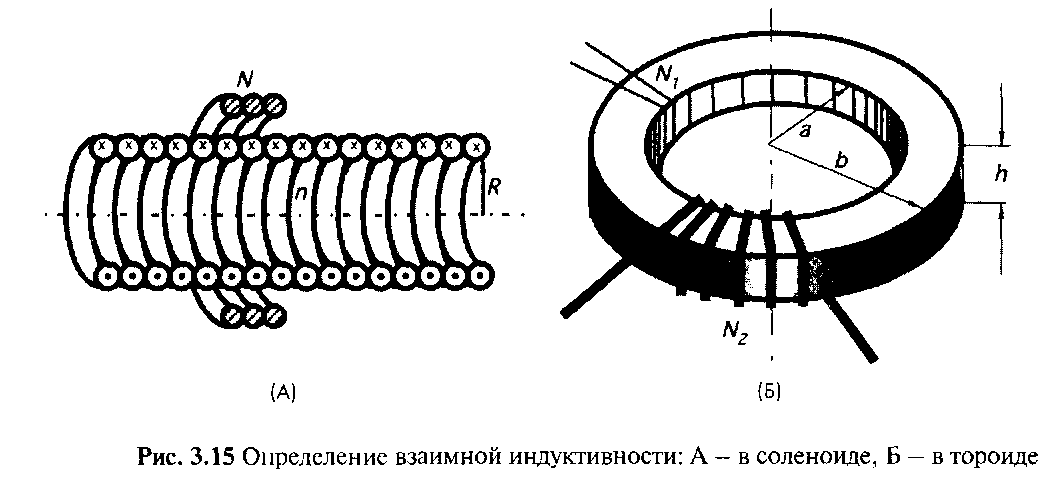
Рис.2.4.1. Определение взаимной индукции: А – в соленоиде; Б - в тороиде.