2.9. Температурные, теплопередающие и тепловые свойства материалов

Все твердые объекты с ростом температуры увеличиваются в объеме, что проис­ходит в результате колебательного движения атомов и молекул. При увеличении температуры среднее расстояние между атомами растет, что приводит к расшире­нию всего твердого тела. Изменение любого линейного размера (длины, ширины или высоты) называется линейным расширением. Длина объекта l₂ при температуре Т₂ связана с первоначальной длиной l₁ соответствующей температуре Т₁, следую­щим соотношением:

(2.9.1)

где α называется коэффициентом линейного расширения. Для разных материа­лов значения а неодинаковые. Этот коэффициент определяется как:

(2.9.2)

где ΔТ= Т₂ — Т₁. Строго говоря, коэффициент а зависит от действитель­ной температуры. Однако для большинства практических применений неболь­шими изменениями α можно пренебречь. Для, так называемых, изотропных материалов, коэффициенты расширения в любом направлении равны. Неболь­шие изменения площади объекта и его объема с высокой степенью точности можно выразить при помощи следующих выражений:

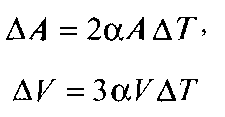(2.9.3)

Тепловое расширение — очень полезное физическое явление, на основе которого ре­ализовано много датчиков, которые либо измеряют тепловую энергию, либо исполь­зуют ее в качестве сигнала возбуждения. Рассмотрим многослойную структуру, со­стоящую из двух пластин X и У, склеенных друг с другом (рис.2.9.1А). Пластины име­ют одинаковые толщину и площадь поверхности и идентичные модули упругости, но разные коэффициенты теплового расширения α₁ и α₂ (α₁ > α₂). Пластины прикрепле­ны с левой стороны к опорной стене. При нагреве пластин, т.е. изменении их темпе­ратуры с Т₁ до Т₂, пластина X увеличится больше, чем пластина У. Зона скрепления двух пластин не позволит пластине X расширяться равномерно, одновременно, зас­тавляя пластину У, увеличиваться больше, чем требует ее коэффициент α. Все это приводит к возникновению внутреннего напряжения, в результате которого структу­ра прогибается вниз. И, наоборот, в случае охлаждения пластин вся структура изог­нется вверх. Радиус изгиба можно оценить при помощи выражения:

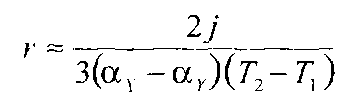(2.9.4)

В результате изгиба максимальное отклонение наблюдается на свободном конце конструкции. Это отклонение может служить мерой изменения температуры. Фактически, биметалличес­кая структура является преобразователем температуры в перемещение.

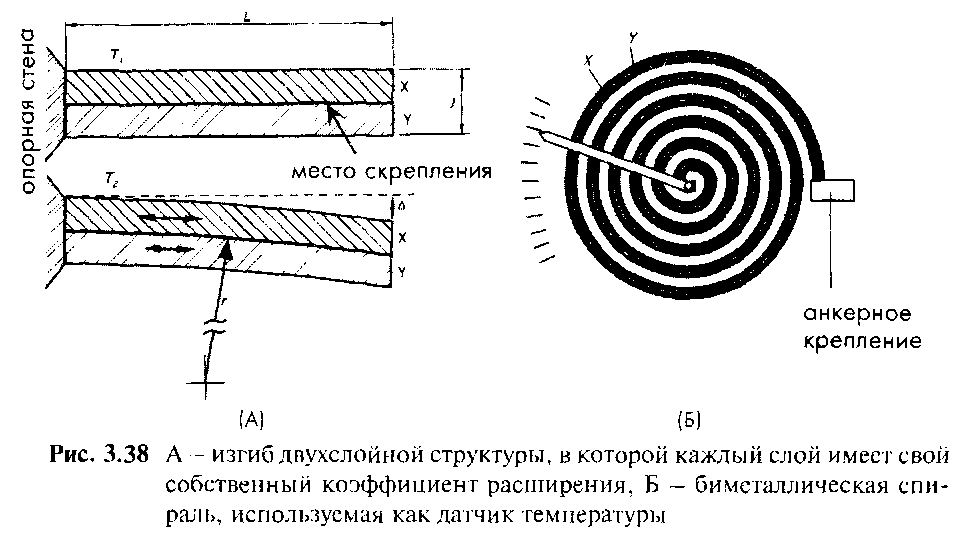
Рис.2.9.1. А – изгиб двухслойной структуры, в которой каждый слой имеет свой собственный коэффициент расширения; Б – биметаллическая спираль, используемая как датчик температуры.

Однако для измерения небольших тем­пературных изменений биметаллические пластины не подходят, поскольку име­ют очень большой радиус изгиба (несколько метров) и, следовательно, очень ма­ленькие отклонения конца структуры. Отклонение конца биметаллической пла­стины можно определить при помощи формулы:

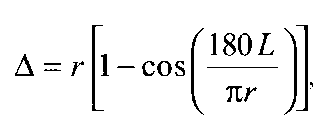(2.9.5)

где r находится из уравнения, a L соответствует длине пластины.

Когда объект нагревается, его температура повышается. Под нагревом подразу­мевается передача объекту определенного количества тепла или тепловой энер­гии. Тепло в объекте накапливается в виде кинетической энергии вибрации ато­мов. Любой объект можно характеризо­вать теплоемкостью, которая зависит как от материала объекта, так и от его мас­сы m:

(2.9.6)

где с — константа, определяемая тепловыми свойствами материала. Она называ­ется удельной теплоемкостью, и для нее справедливо следующее соотношение:

(2.9.7)

Удельная теплоемкость описывает сам материал, в то время как теплоемкость явля­ется характеристикой объекта, сделанного из этого материала. Строго говоря, удель­ная теплоемкость не является постоянной величиной во всем температурном диа­пазоне, включая все состояния материала. Она может существенно меняться при изменении состояния материала, например, при переходе от твердой фазы к жидкой. На микроскопическом уровне удельная теплоемкость отражает струк­турные изменения материала. Было отмечено, что самая низкая удельная теплоемкость воды соответствует 37°С: био­логически оптимальной температуре всех теплокровных животных.

(2.9.8)

Можно отметить, что, как правило, чем тяжелее материал, тем ниже его удельная теплоемкость.

Существуют два фундаментальных свойства теплоты, которые необходимо знать:

• у тепла нет никаких специфических характеристик; это означает, что оно мо­жет иметь разную физическую природу, его можно измерить, но при этом его невозможно различить;

• тепло невозможно ограничить, это означает, что оно свободно передается от теплых частей системы к холодным.

Тепловая энергия может быть передана от объекта к объекту тремя способа­ми, теплопроводностью, конвекцией и излучением. Один из объектов, получаю­щий или отдающий тепло, может быть детектором тепла. Его функция заключа­ется в измерении количества теп­ла, поглощаемого или выделяе­мого объектом, для получения определенной информации об этом объекте. Такой информаци­ей может быть температура объекта, теплота химических ре­акций, расположение или пере­мещение объектов и тд.

Рис.2.9.2. Температурный профиль многослойной структуры.

Рассмотрим многослойную структуру в виде сэндвича, где каждый слой выполнен из разно­го материала. При прохождении тепла через слои температурный профиль структуры будет опре­деляться толщиной каждого слоя и его теплопроводностью. На рис.2.9.2 показана трехслойная структура, в которой первый слой контактирует с источником тепла (устройством, обладающим бесконечной теплоемкостью и высокой теплопроводностью). Одним из самых подходящих твердых объектов, который ведет себя как «бесконечный» источник тепла, считается медное тело большого объема с контролируемой темпе­ратурой. Температура внутри источника тепла постоянная и высокая, за исключе­нием очень узкой зоны, расположенной рядом со слоевой структурой. Тепло пере­дается от материала к материалу через механизм теплопроводности. Скорость па­дения температуры внутри каждого слоя определяется тепловыми свойствами ма­териала. Последний слой отдает тепло в воздух через механизм конвекции и окру­жающим объектам при помощи ИК излучения. Таким образом, рис.2.9.2 иллюст­рирует все три возможных способа передачи тепла от одного объекта к другому.

Для передачи тепла через механизм теплопроводности необходимо обеспечить контакт между двумя объектами. Термически возбужденные частицы теплого тела совершают энергичные колебательные движения и передают кинетическую энер­гию частицам более холодного тела, которые при этом переходят в возбужденное состояние. В результате теплый объект теряет тепло, а холодный — поглощает его. Передача тепла по механизму теплопроводности аналогична потоку воды или элек­трическому току. Например, прохождение тепла через стержень описывается вы­ражением, похожим на закон Ома. Скорость теплового потока через поперечное сечение площадью А (тепловой «ток») пропорциональна градиенту температуры (тепловому «напряжению») по длине стержня (dT/dx):

(2.9.9)

где к называется коэффициентом теплопроводности материала. Знак минус озна­чает, что тепло течет в направлении уменьшения температуры. Хорошие провод­ники тепла обладают высокими коэффициентами к (большинство металлов), в то время как хорошие теплоизоляторы — низкими. Коэффициент теплопроводнос­ти материалов считается константой, хотя, на самом деле, он несколько увеличи­вается с ростом температуры. Для вычисления тепловых потерь за счет теплопро­водности, например, через провод, необходимо знать температуру на обоих его концах: Т₁ и Т₂:

(2.9.10)

где L — длина провода. На практике часто вместо коэффициента теплопроводно­сти используется тепловое сопротивление, определяемое как:

(2.9.11)

В этом случае уравнение (2.9.10) принимает вид:

(2.9.12)

На рис.2.9.2 показан идеальный температурный профиль внутри многослойной структуры, состоящей из материалов с разной теплопроводностью. Если соединить вместе два материала и понаблюдать за распространением тепла в такой конструкции, полученный температурный профиль может выглядеть, как пока­зано на рис.2.9.3А. Если боковые поверхности соединяемых объектов имеют хорошую изоляцию, в стационарных условиях тепловые потоки в обоих материалах должны быть равны. Резкое падение температуры в зоне контакта, площадь которого равна δ, объяс­няется наличием теплового переходного сопротивления. Передачу тепла через двухслой­ную структуру можно описать следующим выражением:

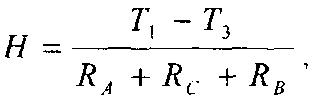(2.9.13)

где R_A и R_B — тепловые сопротивления двух материалов, a R_С — переходное сопротивление:

(2.9.14)

Величина h_C называется переходным коэффициентом. Для некоторых типов дат­чиков, в которых есть механические соединения элементов из двух разных мате­риалов, этот коэффициент играет большое значение. Под микроскопом зона со­единения может выглядеть, как показано на рис.2.9.3Б. Поскольку реальные по­верхности никогда не бывают идеально гладкими, все неровности на них влияют на величину переходного сопротивления.

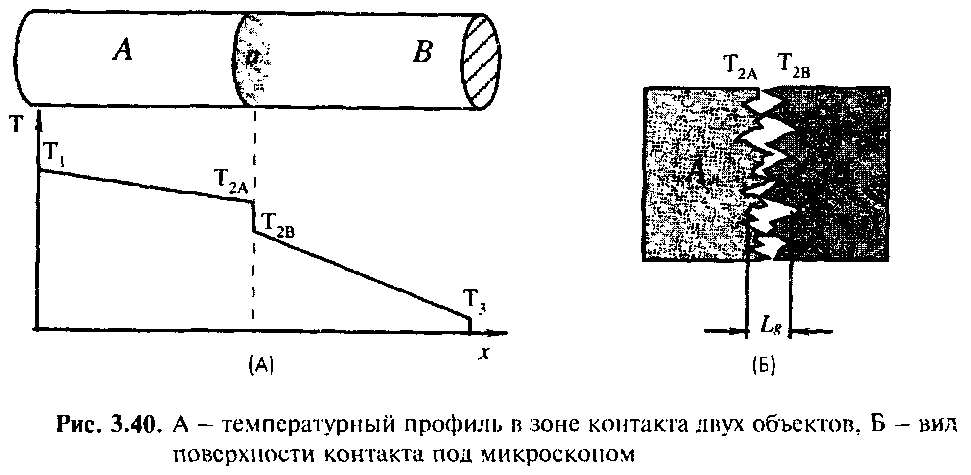
Рис.2.9.3. А – температурный профиль в зоне контакта двух объектов; Б – вид поверхности контакта под микроскопом.

Передача тепла в зоне контакта определяется следующими факторами:

1. Теплопроводностью реального физического соединения двух материалов.

2. Теплопроводностью газов (воздуха) в порах, созданных неровностями повер­хностей.

Поскольку теплопроводность газов, как правило, гораздо меньше теплопровод­ности твердых материалов, газ в порах и создает наибольшее сопротивление при передаче тепла. Поэтому выражение для переходного коэффициента можно за­писать в виде:

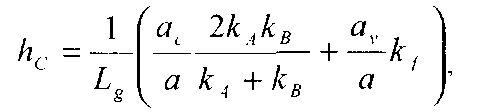(2.9.15)

где L_g — толщина пористой зоны, к_f— коэффициент теплопроводности газов, заполня­ющих поры, a_c и a_v — площади зон контактов и пор, а к_А и к_В — коэффициент теплопро­водности соответствующих материалов. Эту формулу довольно сложно применять на практике из-за трудности экспериментального определения площадей a_c и a_v и рассто­яния L . Однако, анализируя формулу, можно сделать следующий вывод: пере­ходное сопротивление увеличивается при уменьшении давления окружающих газов. С другой стороны, переходное сопротивление уменьшается с ростом давления в зоне со­единения, что связано с деформацией высоких выступов на контактных поверхностях, из-за чего происходит увеличение а_С , а, значит, и создание большей площади контакта между материалами. Для уменьшения теплового сопротивления следует избегать сухо­го контакта между элементами системы, поэтому перед соединением двух поверхнос­тей их рекомендуется покрывать жидкостью, имеющей низкое тепловое сопротивле­ние. Для этой цели часто применяется силиконовая смазка.

Другим способом передачи тепла является конвекция. Для нее требуется промежу­точный агент (жидкость или газ), который забирает тепло у теплого объекта, пере­носит его до холодного объекта, отдает тепловую энергию и после этого возвраща­ется (а может и нет) к теплому объекту за новой порцией тепла. Передача тепла от твердого тела подвижному агенту или внутри подвижного агента также называется конвекцией. Конвекция может быть естественной (под действием сил тяжести) или искусственной (выполняемой механическим путем). При естественной конвекции воздуха на его молекулы действуют две силы, сила тяжести и выталкивающая сила. Теплый воздух поднимается вверх, унося с собой тепло от горячих поверхностей. Более холодный воздух опускается вниз к теплым объектам. Искусственная кон­векция воздуха осуществляется при помощи фена или вентилятора. Она также орга­низуется в жидкостных термостатах для поддержания требуемого уровня темпера­туры внутри устройства. Эффективность передачи тепла конвективным способом определяется скоростью движения промежуточного агента, градиентом температу­ры, площадью поверхности объекта и тепловыми свойствами окружающей среды. Объект, температура которого отличается от внешней температуры, будет получать или отдавать тепло, что можно описать при помощи уравнения, похожего на выра­жение передачи тепла по механизму теплопроводности:

(2.9.16)

где α— коэффициент конвекции, определяемый удельной теплоемкостью теку­чей среды (жидкости или газа), ее вязкостью и скоростью движения. Этот коэф­фициент зависит не только от силы тяжести, но и от градиента температур. Для пластины, расположенной горизонтально в воздухе, значение α можно оценить при помощи следующей формулы:

(2.9.17)

а для пластины, расположенной вертикально, формула принимает вид:

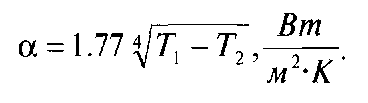(2.9.18)

Следует отметить, что эти выражения годятся только для одной стороны пласти­ны, здесь предполагается, что пластина представляет собой поверхность беско­нечного источника тепла (т.е. ее температура не зависит от потерь тепла), а окру­жающая среда имеет постоянную температуру. Если объем воздуха мал, напри­мер, воздушный зазор между двумя поверхностями разной температуры, движе­ние молекул газа становится очень ограниченным, тогда конвективной переда­чей тепла можно пренебречь. В этом случае передача тепла осуществляется через теплопроводность воздуха и излучение.

Как было отмечено ранее, любой объект, атом и молекула совершают колебательные движения. Средняя кинетическая энергия вибрирующих частиц связана с абсолютной температурой. По законам термодинамики движущийся электрический заряд вызыва­ет появление переменного электрического поля, которое приводит к образованию пе­ременного магнитного поля. В свою очередь, в результате изменений в магнитном поле происходят перемены и в связанном с ним электрическом поле и т.д. Таким образом, вибрирующие частицы являются источниками электромагнитного поля, подчиняю­щегося законам оптики и распространяющегося со скоростью света. Электромагнит­ные волны могут отражаться, фильтроваться, фокусироваться и т.д. На рис.2.9.4 пока­зан полный спектр электромагнитного излучения: от γ-лучей до радиоволн.

Длина волны связана с частотой ν и скоростью света в конкретной среде с:

(2.9.19)

Зависимость между длиной волны и температурой подчиняется закону Планка, открытому в 1901 году (в 1918 году немецкий физик Планк был удостоен Нобе­левской Премии за открытие энергии кванта). Планк установил зависимость между плотностью потока излучения W_λ, длиной волны λ и абсолютной темпе­ратурой Т. Плотность потока излучения — это мощность электромагнитного по­тока на единицу длины волны:

(2.9.20)

где ε(λ) — излучающая способность объекта, С₁=3,74*10^-12 Вт*см² и С₂=1,44см*К — константы, а е — основание натурального логарифма.

Температура — это результат осреднения кинетических энергий огромного количества вибрирующих частиц.

Однако не все частицы вибрируют с одинако­вой частотой и амплитудой. Разрешенные частоты (а также длины волн и энер­гии) расположены очень близко друг к другу, поэтому количество частот, на кото­рых могут излучать различные материалы, является практически бесконечной величиной. Длины излучаемых волн бывают любыми: от очень длинных до очень коротких. Поскольку температура является статистическим выражением средней кинетической энергии, она определяет наиболее вероятную частоту и длину вол­ны колеблющихся частиц. Наиболее вероятная длина волны определяется зако­ном Вина (в 1911 году немецкому ученому Вильгельму Вину была присуждена Но­белевская премия за открытие законов теплового излучения). Для ее нахождения надо приравнять нулю первую производную от уравнения. В результате вычислений можно получить длину волны, в окрестностях которой происходит наибольшая мощность излучений:

(2.9.21)

где λ_m измеряется в мкм, а Т - в Кельвинах. Закон Вина утверждает, что чем выше температура, тем короче становиться длина волны излучений (рис.2.9.4).

Рис.2.9.4. Спектр электромагнитного излучения.

С уче­том уравнения (2.9.19) можно сделать вывод, что наиболее вероятная частота из­лучения пропорциональна абсолютной температуре.

(2.9.22)

Например, при нормальной комнатной температуре большая часть ИК энергии излучается от объектов с частотой около 30 ТГц. Частота излучения и длина волны определяются только температурой, тогда как амплитуда излучения еще зависит и от излучающей способности поверхности ε(λ).

Для того чтобы определить полную мощность излу­чения в конкретном интервале длин волн, необходимо проинтегрировать уравне­ние внутри указанного диапазона, от А₁ до А₂

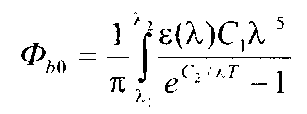(2.9.23)

На рис.2.9.5 показана плотность потока излучений идеального излучателя (λ₁ =0; λ₂=∞) для трех разных темпера­тур. Из рисунка видно, что мощность излучения распределяется в спектраль­ном диапазоне очень неравномерно, а ее максимум соответствует максимуму, определенному по закону Вина горя­чий объект излучает значительную часть своей энергии в видимом диапазоне, а мощность, излучаемая более холодны­ми объектами, смещается в ИК и даль­ний ИК диапазоны спектра.

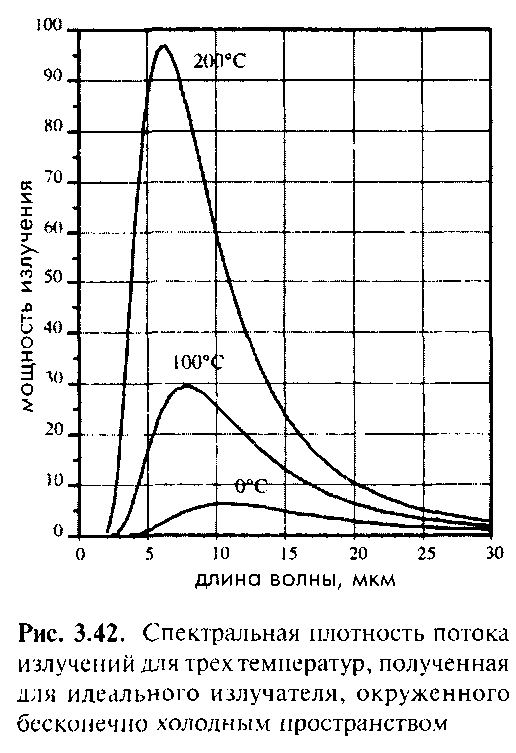
Рис.2.9.5. Спектральная плотность потока излучений для трех температур, полученная для идеального излучателя, окруженного бесконечно холодным пространством.

Уравнение очень сложное, и его практически невозможно решить аналитически. Решение может быть по­лучено либо численными методами, либо при помощи аппроксимаций. Ап­проксимация в широкой полосе спект­ра (когда λ₁ и λ₂ охватывают более 50% всей излучаемой мощности) в виде па­раболы четвертого порядка известна под названием закона Стефана-Больцмана:

(2.9.24)

Здесь σ — 5,67*10^-8Вт/м²К⁴ - постоянная Стефана-Больцмана, А — пло­щадь излучающей поверхности, а е считается независимой от длины волны.

В то время как длина волны излучаемого света зависит от температуры, амплитуда излучения является функцией от излучающей способности поверх­ности, часто называемой коэффициентом излучения которая изменяется в ди­апазоне 0...1. Этот коэффициент является отношением потока излучений, ис­ходящего от поверхности, к потоку излучений от идеального излучателя при той же самой температуре. Было выведено фундаментальное соотношение, свя­зывающее коэффициент излучения ε, коэффициент отражения ρ и коэффи­циент пропускания γ.

(2.9.25)

В 1860 году Кирхгоф обнаружил, что излучающая и поглощающая способности являются одной и той же физической величиной. Поэтому для абсолютно черно­го тела (γ=0) выражение может быть записано в виде:

. (2.9.26)

Закон Стефана-Больцмана опре­деляет мощность излучения, испуска­емого поверхностью с температурой Т в бесконечно холодное пространство с температурой, равной абсолютному нулю.

Излучающая способность среды является функцией ее диэлектрической про­ницаемости и, следовательно, коэффициента преломления n. Максимальная излучающая способность равна 1. Она соответствует, так называемому, чер­ному телу — идеальному источнику электромагнитных излучений. Причиной такого названия является внешний вид объектов при нормальной комнат­ной температуре. Если тело является непрозрачным (γ=0) и ничего не отра­жает (ρ=0), то согласно уравнению оно представляет собой идеаль­ный источник и поглотитель электромагнитных излучений (поскольку α=ε). Однако следует отметить, что излучающая способность объекта, как пра­вило, зависит от длины волны излучений (рис.2.9.6). Часто излучающую способность в сравнительно узком спектральном ди­апазоне тепловых излучений (например, от 8 до 16 мкм) считают постоянной величиной. Однако для прецизионных измерений, когда тепловое излучение необходимо определять с точностью лучше 1%, излучающая способность по­верхности должна быть либо заранее известна, либо надо использовать двухдиапазонный ИК детектор (Этот детектор проводит измерение потока ИК излучений в двух узких спектральных диапазонах. Далее по отношению двух сигналов определяют температуру объекта. В процессе вычислений коэффи­циент излучения и другие мультипликативные составляющие сокращаются).

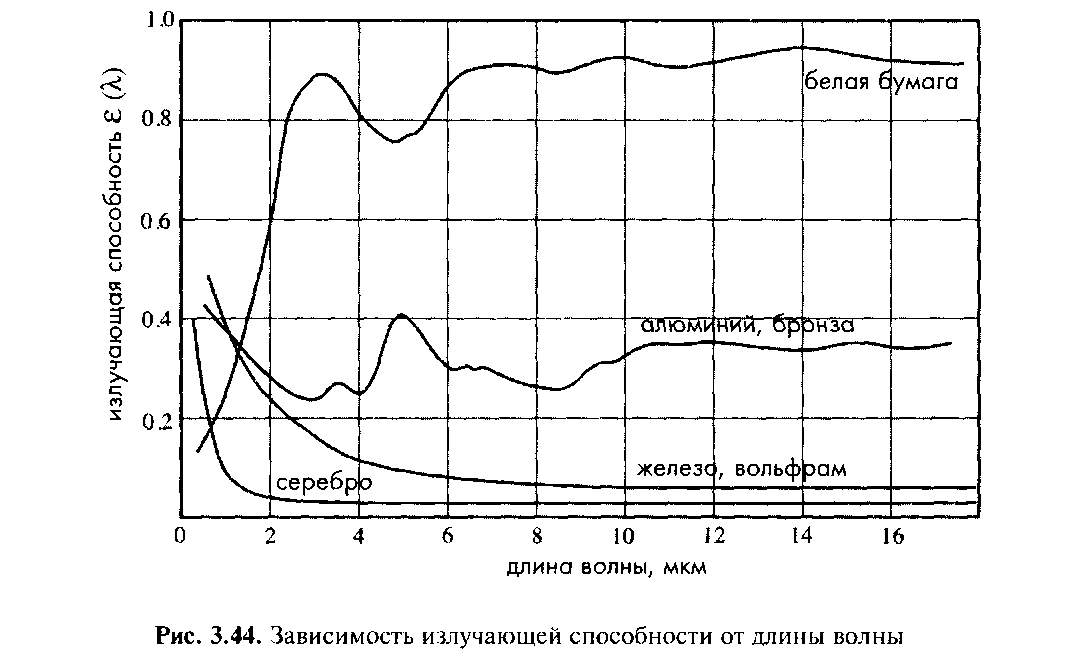
Рис.2.9.6. Зависимость излучающей способности от длины волны.

Для неполяризованного света дальнего ИК диапазона, направленного пер­пендикулярно поверхности, можно записать следующее выражение для коэффи­циента излучения:

(2.9.27)

Все неметаллические материалы являются очень хорошими источниками диффу­зионного теплового излучения, обладающими практически постоянной излучаю­щей способностью в пределах телесного угла ±70°, определяемой уравнением. За границами этого угла вплоть до 90° коэффициент излучения стремительно пада­ет. В окрестности 90° он равен практически 0. На рис.2.9.7А показана типичная для неметаллических материалов диаграмма направленности излучений в воздухе. Сле­дует подчеркнуть, что все вышесказанное справедливо только для длин волн даль­него ИК диапазона спектра, и совсем несправедливо для волн видимого света.

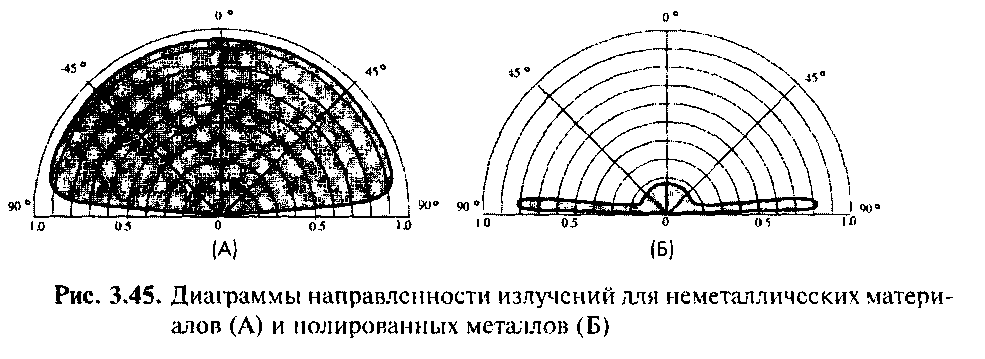
Рис.2.9.7. А – диаграммы направленности излучений для неметаллических материалов; Б - диаграммы направленности излучений для полированных металлов.

Металлы ведут себя совсем по-другому. Их излучающая способность силь­но зависит от способа обработки поверхности. Как правило, хорошо отшлифо­ванные металлы плохо излучают в пределах телесного угла ±70°, а при больших углах их излучающая способность значительно возрастает (рис.2.9.7Б). Это оз­начает, что даже очень хорошие зеркала плохо отражают при углах в окрестнос­ти 90° от нормали.

В отличие от большинства твердых тел газы во многих случаях являются прозрачными для теплового излучения. Они поглощают и испускают излуче­ния только определенного узкого спектрального диапазона. Некоторые газы, такие как О₂, N₂ и другие, состоящие из симметричных неполярных молеку­лярных структур, пропускают электромагнитные волны только при низких тем­пературах, тогда как СО₂, Н₂О и углеводородные газы излучают и поглощают волны в более широком диапазоне. При попадании ИК света в слой газа его поглощающая способность падает по экспоненте, подчиняясь закону Ламбер­та-Бера:

(2.9.28)

где Ф₀ — падающий тепловой поток, Ф_х — поток на глубине х, а α_λ — спект­ральный коэффициент поглощения. Это отношение также называется моно­хроматическим коэффициентом пропускания (проницаемостью) опреде­ленной длины волны λ. Если отражающая способность газа равна нулю, его коэффициент излучения определяется в виде:

(2.9.29)

При измерении электромагнитного излучения из углубления, называемого ре­зонатором, наблюдается интересный эффект. Резонатор представляет собой полость произвольной формы внутри тела с равномерной температурой по всей поверхности внутренних стенок (рис.2.9.8А). Излучающая способность апер­туры резонатора (но не его внутренней части!) по сравнению с плоской повер­хностью значительно возрастает, а на некоторых длинах волн приближается к единице. Этот эффект еще более усиливается, если внутренние стенки резо­натора обладают достаточно высоким коэффициентом излучения. Рассмотрим поверхность неметаллического резонатора. Все неметаллы являются диффу­зионными излучателями. Предположим, что температура и излучающая спо­собность резонатора являются одинаковыми в любой его внутренней точке. Идеальный объект, чей коэффициент излучения равен единице, называется черным телом. Черное тело испускает с площади поверхности а поток ИК-фо­тонов, равный:

(2.9.30)

Однако реальный объект имеет коэффициент излучения ε_b, поэтому с точно такой же площади его поверхности испускается меньший поток:

(2.9.31)

Поток, излучаемый другими частями объекта такой же площади а, тоже равен Ф_r (поскольку температура объекта считается везде одинаковой, простран­ственное распределение потока не учитывается). Значительная часть падаю­щего потока Ф_r поглощается поверхностью площади а, в то время как мень­шая часть диффузионно отражается:

(2.9.32)

Сложив излучаемый и отраженный потоки с площади а, получим:

(2.9.33)

Отсюда находим выражение для эффективной излучающей способности:

(2.9.34)

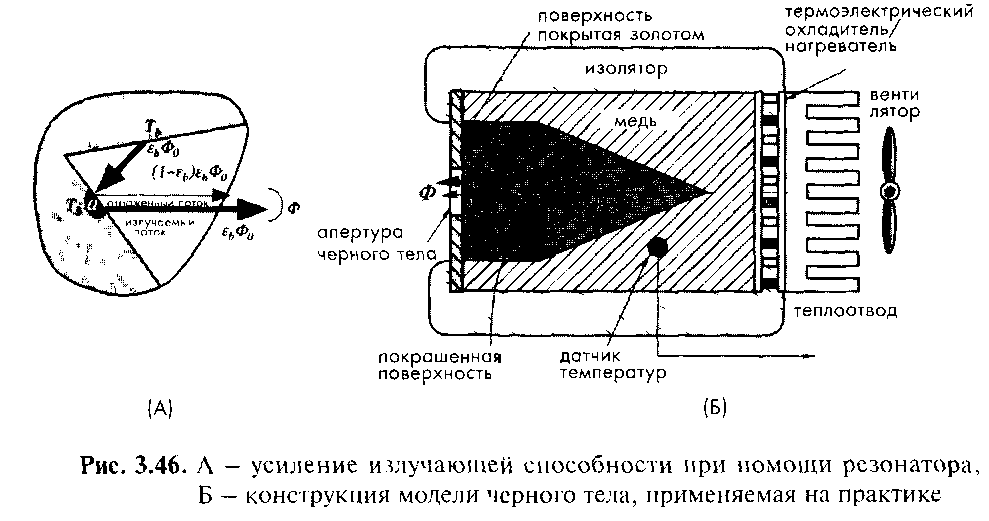
Рис.2.9.8. А – усиление излучающей способности при помощи резонатора; Б – конструкция модели черного тела, применяемая на практике.

Из уравнения видно, что при однократном отражении излучающая способность резонатора увеличивается в (2-ε_b) раза по сравнению с излучением ровной поверхности. Но в резонаторе может происходить несколько переотраже­ний, поэтому поток излучений, падающий на площадку а, представляет собой сумму излучений и отражений от многих частей резонатора. Интенсивность ре­зультирующего потока, как правило, превышает интенсивность исходного пото­ка излучений Ф_r.

Рис.2.9.9. Фотографии в видимом свете и в ИК излучении.

Резонансный эффект меняет реальный коэффициент излучения, что всегда необходимо учитывать для предотвращения возникновения ошибок при оценке излучающей мощности. Рис.2.9.9 иллюстрирует это. На нем показаны две фо­тографии: одна сделана в потоке видимого света, другая — в лучах среднего ИК диапазона (тепловое излучение). Из рисунка видно, что области в районе ноздрей носа выглядят несколько ярче, а значит и теплее, хотя температура этих участков практически не отличается от соседних. Две складки возле усов появились в результате резонансного эффекта, который увеличил излучающую способность кожи в этих местах от 0,96 до более высоких значений. Это уси­лило интенсивность отраженного теплового потока и создало иллюзию более теплой кожи.