68. Неодн. Лин. Ду n-го порядка с пост. Коэф-тами, спец. Прав. Часть.

Лин. неодн. ур-е -го порядка имеет вид

(1)

где , - непр-ны на инт-ле .

Общее реш-е ур-я (1) нах-ся по ф-ле (2)

- общее реш-е лин. одн. ур-я , соответствующего ур-ю (1), а - к-нибудь частное реш-е неодн. ур-я (1)

Опр. ФСР – любые лин. независимых реш-й ур-я .

1. Если сущ. ФСР, то общ. реш-е неодн. ур-я (1) м. б. найдено с пом Метода вариации произвольных постоянных (Лагранжа).Сущность этого метода сост. в след. Общее реш-е неодн. ур-я (1) ищем в виде 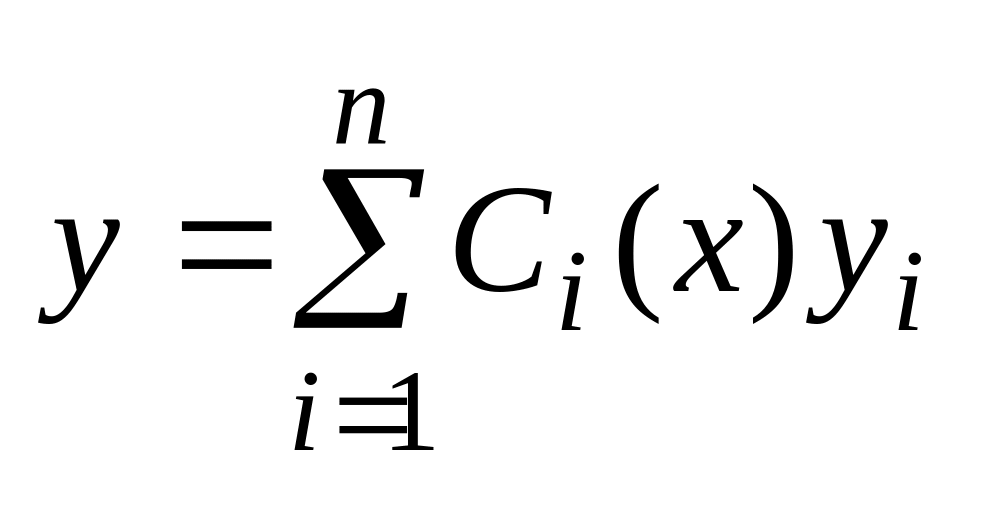(3)

где ф-и опр-ся из сист. ур-й

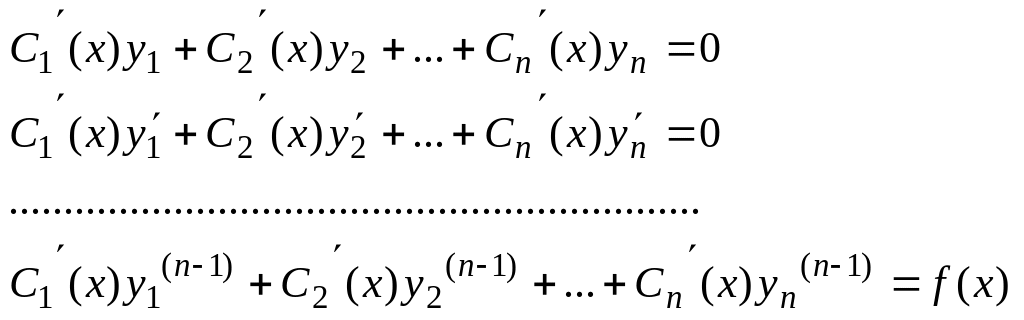(4Относ. (4) явл. сист. лин. неодн. алгебраич. ур-й, причем главный определитель сист.

(5)

Поэтому сист. (4) имеет единств. реш-е:

, (6)

откуда (7)

где - произвольные постоянные. Учитывая рав-ва (3) и (7), общее реш-е неодн. ур-я, найденное методом вариации произвольных постоянных, получаем в виде

(8)

2. Метод неопр коэф-тов.

Пусть , где , - многочлен степени .

1)Если не совпадает ни с одним корнем х-кого ур-я. Тогда

,

где - многочлен той же степени, что и .

2)Если совпадает с корнем х-кого ур-я кратности . Тогда

,

где - многочлен той же степени, что и .

Пусть

1) - не явл. корнем х-кого ур-я

где - многочлен той же степени, что и .

2) - явл. корнем х-кого ур-я

69 Лин. Неодн. Диф. Ур-я 2го порядка с постоянными коэф-ми. Метод вариации произвольных постоянных.

Рассмотрим диф-е ур-е вида:

, (1) где p,q – вещественные числа, f(x) – заданная ф-я от пер-й x.

Для нахождения общего интеграла ур-я (1) достаточно найти частное решение этого неоднородного ур-я и сложить его с общим реш-ем соответствующего однородного ур-я.

Поскольку общий интеграл однородного ур-я известен, можем с помощью квадратор получить частное реш-е неоднородного ур-я, пользуясь методом вариации произвольных постоянных.

Данный метод покажем в частном случае, когда уравнение (1) имеет вид: (2)

Общий интеграл однородного уравнения имеет вид:

Общий интеграл неоднородного ур-я: и

Частное решение неоднородного уравнения будем искать:

(3)

y₁ y₂

В решении (3) v₁ и v₂ есть функции от переменной x. Имея не одну, а две искомые функции, мы можем кроме исходного уравнения подчинить их ещё одному условию.

(4)

То мы имеем систему двух уравнений для отыскания ф-и v₁, v₂.

Продиф-ем соотн-е (3):

Учтём (4): (*)

Учитывая тот факт, что y₁ и y₂ есть решения однородного уравнения (2), т.е. соотношение [ ]=0, будем иметь условие:

Имеем систему для отыскания функции v₁, v₂:

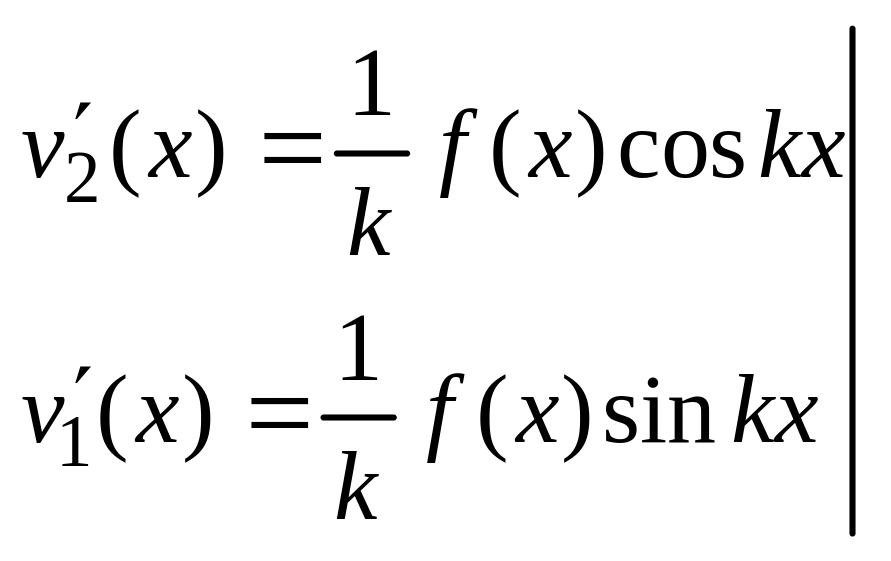
Запишем первообразную функций в виде интегралов с переменным верхним пределом и обозначим переменную через . Тогда:

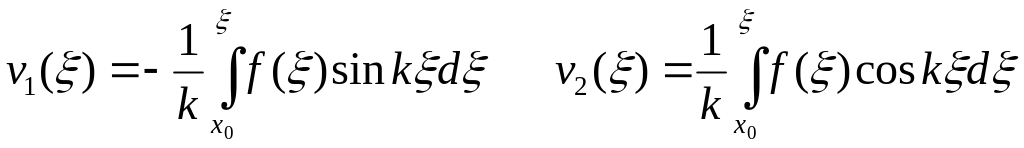, где x₀ – некоторое фиксированное число.

Подставим найденное значение f в решение (3), будем иметь: 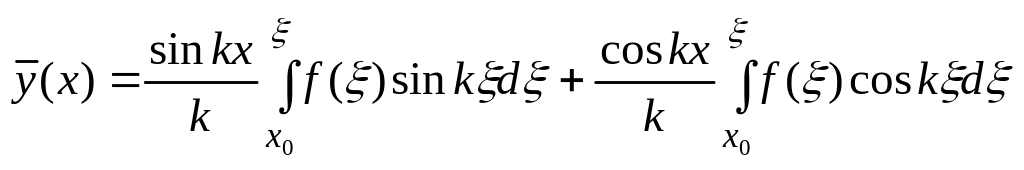Решение можно представить в виде, если ввести множители под знак интегрирования, то получим: .

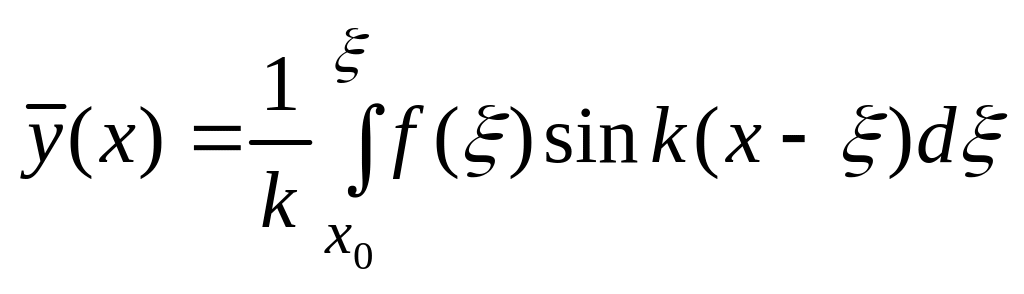Окончательное реш-е исходного неоднородного ур-я будет иметь вид:

(**)

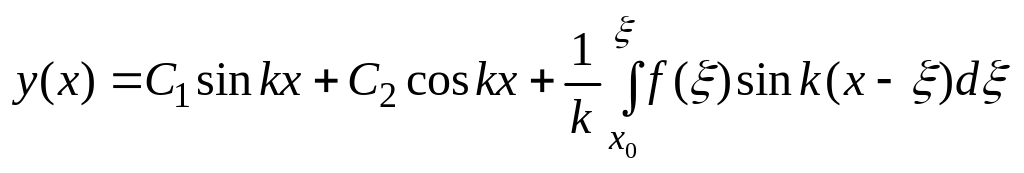Соотношением (**) определено общее решение исходного неоднородного уравнения (2), не содержащего первую производную.

При решении линейных неоднородных уравнений с постоянными коэффициентами во многих случаях удаётся без труда подобрать частное решение и тем самым свести решение задачи к отысканию решения соответствующего его однородного уравнения

Если правая часть представляет собой многочлен n-ой степени, то решение ищется в виде полинома n-ной степени.