65.Многочлены над полями q,r,c. Основная tr алгебры.

Мн-н называется не приводимым над полем Р, если не м. б. представлен в виде произведения двух других мн-нов с коэф-ми из поля Р, степени которых меньше степени данного мн-на.

Мн-н нулевой степени (const) не причисляется ни к приводимым, ни к не приводимым.

Над полем С не приводимы только мн-ны первой степени. Всякий мн-н м/б разложен на лин-ые множители, т.е. всякий мн-н в виде: a₀xⁿ+ a₁x^n-1+…

Над полем R не приводимы только мн-ны 1-ой степени и мн-ны 2-ой степени, не имеющие действит.корней.

Над полем Q существуют не приводимые мн-ны различных степеней.

Пример: xⁿ+2, nєN.

Непроводимость мн-на над Q опр-ся по критерию Эйзенштейна: Если для мн-на n>0 с целыми коэф-ми существует простое число p: старший коэф-т , все остальные коэф-ты , а свободный член , i=1,n. То этот мн-н – не приводим над полем Q.

Пример: 1) x⁴+1 – над Q. 2) x⁴+1= - над R. 3) - над С.

Если степень мн-на > 0 => не разрешимые в радикалах.

Нахождение рацион. Корней мн-на (TR-мы справедливы для мн-нов с целыми коэф-ми):

1)TR1: Если несократимая дробь вида явл-ся корнем мн-на .2) TR2: Если несократимая дробь вида явл-ся корнем мн-на

3)Следствие из TR2: .

TR1(Основная TR-ма алгебры): Всякий мн-н, степени n>=1 с комплексными коэф-ми, имеет хотя бы 1 корень, в общем случае – комплексный.

TR2: Всякий мн-н, степени n>=1 с комплексными коэф-ми, имеет n корней, если каждый корень считать столько раз, какова его кратность.

TR3:Всякий мн-н f(x) с действительными коэф-ми, имеет комплексный корень а, то и число также явл-ся его корнем, где кратность а и совпадают.

TR4:Всякий мн-н f(x) с действительными коэф-ми !-ым образом можна представить в виде произведения нескольких множителей вида (x-a), соответ-щих его действ-ым корням, и квадрат-ых 3-членов , соотв-щих его компл-ым корням. При действ-ых значениях а переменной х все указанные множители будут действительными.

66. Основные типы ду 1-го порядка

ДУ – это ур-е, в кот-м неизв. ф-я или в-р ф-и входит под знаком производной или диф-ла.

Порядок ДУ – макс-й порядок входящей в ур-е производной (диф-ла) неизвестной ф-ии.

1. Ур-я 1-го порядка, разрешаемые относ-но производной.

Обыкн-е ДУ 1-го порядка можно, разрешить относ-но производной, представив в виде:

где с – const. Константа с м. б. определена, если известны знач-я y(x₀)=y₀.

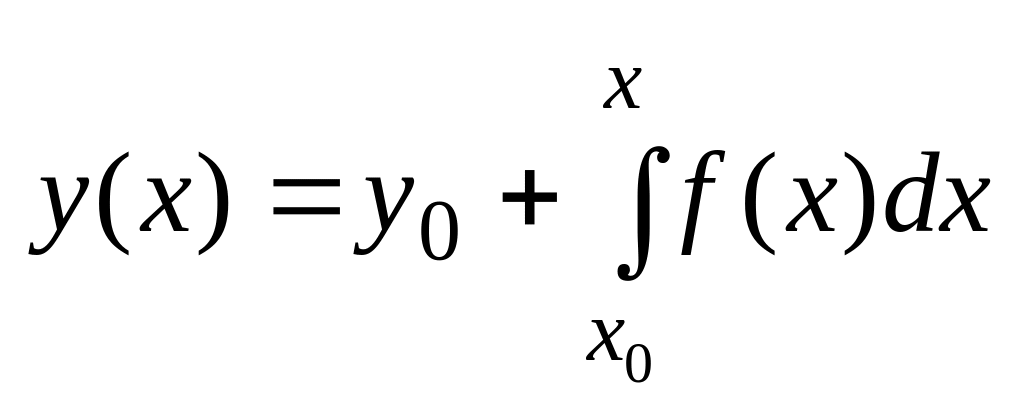
2. Уравнения с разделенными и разделяющимися пер-ми.

Рассмотрим ДУ вида Предполагаем, что f₂(у)0. преобразуем его к виду Пологая y известной ф-ей от x, (2) можно рассматривать как рав-во 2-х диф-лов, тогда неопределенные интегралы от них будут отличаться постоянным слагаемым С. мы получили соотношение, связывающее искомую ф-ю у, независимую переменную х и произвольную постоянную С, т. е. получили общий интеграл (общ. решение) ур-я (2).

ДУ типа M(x)dx+N(y)dy=0 наз. ДУ с разделенными переменными.

Его общее реш-е имеет вид: , а ур-е вида: М₁(х)N₁(y)dx+M₂(x)N₂(y)dy=0 – наз. ДУ с разделяющимися переменными, т. к. путем деления на М₂(х)N₁(y) оно приводится к ур-ю с разделенными переменными

3. Ур-я, приводимые к ур-ям с разделяющимися пер-ми.

Рассм ур-е вида (1), где - нек. константы. Сделаем замену: , тогда . Подставляя (3) и (2) в (1), получим или - ур-е с разделяющимися пер-ми. Рассм ур-е вида , в этом случае

- ур-е с разделяющимися пер-ми.

4. Линейные ур-я 1-го порядка – ур-я, содержащие у и у^’ в первой степени, вида:

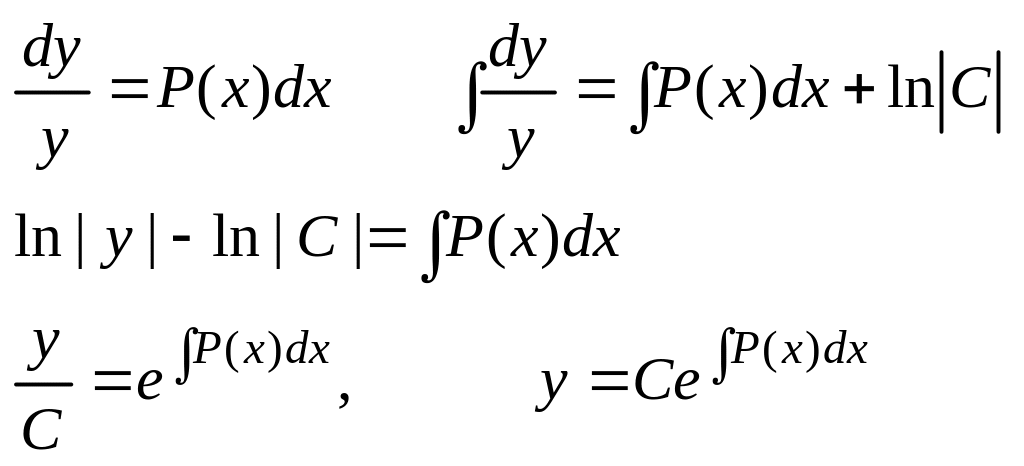Если Q(x)0  такое ур-е наз-ся однородным его реш-е будет иметь вид: К линейным ДУ могут быть сведены некоторые ДУ: