11.Применение первого начала термодинамики к изопроцессам в идеальном газе.

И зохорный процесс (V=const). Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис. 1), где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е. 

Из первого начала термодинамики (δQ=dU+δA) для изохорного процесса следует, что вся теплота, которая сообщается газу, идет на увеличение его внутренней энергии: δQ=dU Для произвольной массы газа:

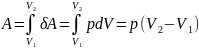
И зобарный процесс (p=const). Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, которая параллельна оси V. При изобарном процессе работа газа при увеличения объема от V₁ до V₂ равна 

и равна площади заштрихованного прямоугольника (рис. 2). Если использовать уравнение Менделеева-Клапейрона для выбранных нами двух состояний, то 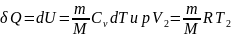 откуда Тогда выражение (2) для работы изобарного расширения примет вид

Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля—Мариотта: 

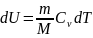
Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, которая расположена на диаграмме тем выше, чем выше температура, при которой происходит процесс. 

Исходя из формул для работы газа и уравнения Менделеева-Клайперона найдем работу изотермического расширения газа: 

Так как при Т=const внутренняя энергия идеального газа не изменяется: то из первого начала термодинамики (δQ=dU+δA) следует, что для изотермического процесса δQ=δA т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил:

12.Адиабатический процесс. Уравнение Пуассона и показатель адиабаты. Термодинамические функции состояния.

Адиабатическим называется процесс, при котором отсутствует теплообмен (δQ=0) между системой и окружающей средой. Адиабатическим процессами можно считать все быстропротекающие процессы.

Из первого начала термодинамики (δQ=dU+δA) для адиабатического процесса следует, что δA=- dU (1)т. е. внешняя работа совершается за счет изменения внутренней энергии системы.

Используя формулы δA=pdV и C_V=dU_m/dT, для произвольной массы газа перепишем уравнение (1) в виде: 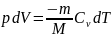(2) применив дифференцирование уравнение состояния для идеального газа получим: 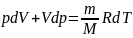(3)

Исключим из (2) и (3) температуру Т.  Разделив переменные и учитывая, что , найдем 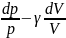 . Проинтегрируя это уравнение в пределах от p₁ до p₂ и соответственно от V₁ до V₂, и потенцируя, придем к выражению  или

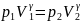
Так как состояния 1 и 2 выбраны произвольно, то можно записать , полученное выражение есть уравнение адиабатического процесса, называемое также уравнением Пуассона.

  называется показателем адиабаты (или коэффициентом Пуассона). работа при адиабатическом процессе.

13. Круговые процессы. Обратимые и необратимые процессы. Тепловая машина. Кпд теплового двигателя.

Круговым процессом(циклом) называется такой процесс, в результате которого термодинамическая система возвращается в исходное состояние.

Обратимым процессом называют такой процесс, который может быть проведен в обратном направлении таким образом, что система будет проходить через те же состояния, что и при прямом ходе, но в обратной последовательности. Обратимым может быть только равновесный процесс.

В том случае, когда после завершения прямого и обратного процессов система вернулась в первоначальное состояние и в окружающей среде остались изменения, процесс является необратимым. Очевидно, что все процессы в природе необратимые.

Тепловая машина-устройство, преобразующее тепловую энергию в механическую работу (тепловой двигатель) или механическую работу в тепло (холодильник). Преобразование осуществляется за счёт изменения внутренней энергии рабочего тела — на практике обычно пара или газа.

Идеальная тепловая машина — машина, в которой произведённая работа и разница между количеством подведённого и отведённого тепла равны. Работа идеальной тепловой машины описывается циклом Карно.

При работе часть тепла Q1 передается от нагревателя к рабочему телу, а затем часть энергии Q2 передается холодильнику, который охлаждает машину КПД тепловой машины считается по формуле (Q1-Q2/Q1)х100

Периодически действующий двигатель, совершающий работу за счет получаемого извне тепла, называется тепловой машиной.

Коэффициент полезного действия (КПД) теплового двигателя рассчитывается как отношение работы, совершаемой двигателем, к количеству теплоты, полученному от нагревателя: