Одношаговые методы решения задачи Коши

Метод Эйлера

Это простейший метод решения задачи Коши, позволяющий интегрировать дифференциальные уравнения первого порядка. Его точность невелика, и поэтому на практике им пользуются сравнительно редко. Однако на основе этого метода легче понять алгоритм других, более эффективных методов.

Найдём приближенное решение уравнения (12.3) на отрезке [x_0, b],  удовлетворяющее начальному условию y=y₀ при x=x₀. Разделим отрезок [x_0,b],  точками  на n равных частей (рис. 12.1).

Рис. 12.1

Обозначим ,т.е. . В этом методе  заменяется приближенной формулой:

                                                                                                      (12.5)

В результате на первом отрезке [x_0, x₁] искомое решение приближенно представляется формулой:

, .

Здесь x₀ , y₀ , h известны, следовательно, находим:

Иными словами на отрезке [x_0, x₁]  искомая интегральная кривая (точное решение) заменяется отрезком прямой M₀M₁  касательной к кривой в точке M₀. Тангенс угла наклона этой прямой равен f(x₀, y₀). Аналогично находятся остальные приближенные значения:

                                                (12.6)

Ошибка метода имеет порядок  h².

Модифицированный метод Эйлера

Хотя тангенс угла наклона касательной к истинной кривой в исходной точке известен и равен , он известен в соответствии с изменением независимой переменной. Поэтому в точке x₀ +h наклон касательной уже не таков, каким он был в точке x₀. Следовательно,     при     сохранении     шага наклона касательной на всем интервале h  в результаты  вычисления  вносится погрешность. Точность    метода    Эйлера можно   существенно   повысить, улучшив аппроксимацию производной. Это можно   сделать, используя среднее значение производной в начале и в конце интервала. В модифицированном методе Эйлера сначала вычисляется значение функции в следующей точке по методу Эйлера:

,

которое используется для вычисления приближенного значения в конце интервала . Вычислив среднее между этим значением производной и её значением в начале интервала, найдем более точное значение y_n+1:

                          (12.7)

 Это соотношение описывает модифицированный метод Эйлера. Ошибка на каждом шаге при использовании этого метода, имеет порядок h³. За повышение точности приходится расплачиваться дополнительными затратами математического времени, необходимыми для вычисления .

Метод Рунге - Кутта

Существует и другие явные одношаговые методы. Наиболее распространенным из них является метод Рунге - Кутта. На его основе могут быть построены разностные схемы разного порядка точности. Приведем схему Рунге - Кутта четвертого порядка:

      

где

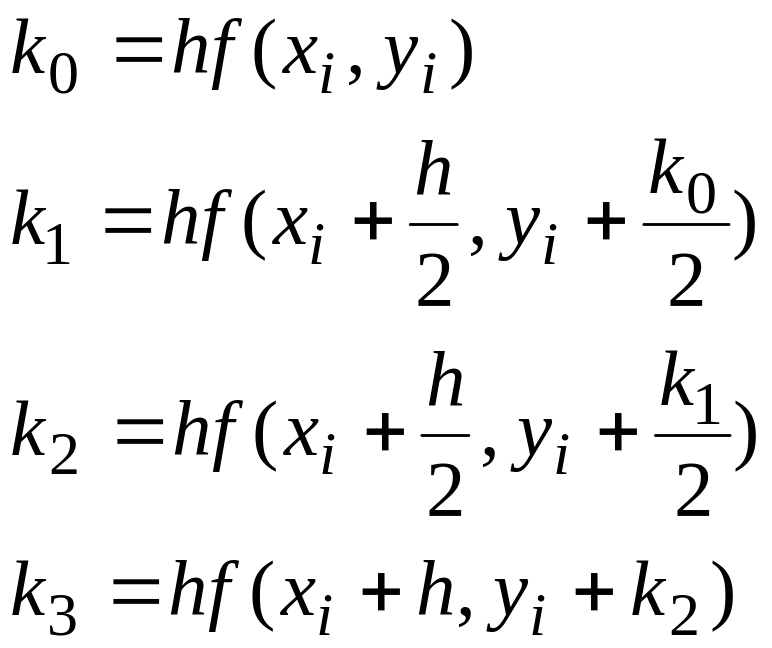                                        (12.8)

Таким образом, метод Рунге - Кутта требует на каждом шаге четырёхкратного вычисления правой части уравнения f(x, y). Метод Эйлера и его модифицированный вариант так же могут рассматриваться как методы Рунге - Кутта первого и второго порядков. Метод Рунге - Кутта требует большого объема вычислений, однако это окупается повышенной точностью, что даёт возможность проводить счет с большим шагом. Другими словами, для получения результатов с одинаковой точностью в методе Эйлера потребуется значительно меньший шаг, чем в методе Рунге - Кутта.