Санкт-Петербургский государственный электротехнический университет.

Кафедра МОЭВМ

Дисциплина «Вычислительная математика»

Отчет по лабораторным работам № 3-6

Преподаватель: Лисс А. Р.

Cтуденты гр. 2351: Баскаков Ю. Н.

Санкт-Петербург

2004

1. Постановка задачи.

Найти корень уравнения с заданной точностью методами бисекции, хорд, Ньютона и простых итераций. Исследовать обусловленность методов и зависимость числа итераций от точности результата.

2. Выполнение лабораторных работ.

1) Исследуемая функция: .

2) График функции f(x):

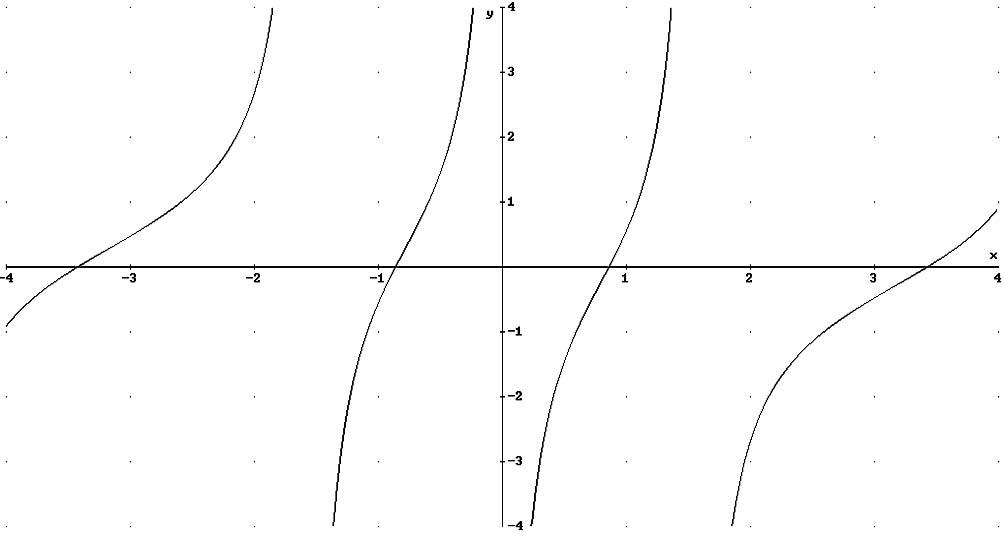
Графически отделили корень уравнения . Функция удовлетворяет условиям применимости методов бисекции, хорд, Ньютона и простых итераций на отрезке [0.5, 1].

3) Метод бисекции.

Если найден отрезок [a,b], такой, что (a)(b)<0, существует точка c, в которой значение функции равно нулю, т.е. (с)=0, сÎ(a,b). Метод бисекции состоит в построении последовательности вложенных друг в друга отрезков, на концах которых функция имеет разные знаки. Каждый последующий отрезок получается делением пополам предыдущего. Процесс построения последовательности отрезков позволяет найти нуль функции (корень уравнения ) с любой заданной точностью.

Рассмотрим один шаг итерационного процесса. Пусть на (n-1)-м шаге найден отрезок [a_n-1, b_n-1][a, b], такой, что (a_n-1)(b_n-1). Разделим его пополам точкой (a_n-1 +b_n-1)/2 и вычислим (). Если ()=0, то =( a_n-1+b_n-1)/2- корень уравнения. Если (), то из двух половин отрезка выбирается та, на концах которой функция имеет противоположные знаки, поскольку искомый корень лежит на этой половине, т.е.

a_n=a_n-1, b_n= , если ()(a_n-1) < 0 ;

a_n=, b_n= b_n-1 , если ()(a_n-1) > 0 .

Если требуется найти корень с точностью , то деление пополам продолжается до тех пор, пока длина отрезка не станет меньше 2. Тогда координата середины отрезка есть значение корня с требуемой точностью .

Метод бисекции является простым и надежным методом поиска простого корня уравнения (простым называется корень x=c дифференцируемой функции , если (с) и (с)). Этот метод сходится для любых непрерывных функций , в том числе недифференцируемых. Скорость его сходимости невысока. Для достижения точности  необходимо совершить Nlog₂(b-a)/ итераций. Это означает, что для получения каждых трех верных десятичных знаков необходимо совершить около 10 итераций.

Исходные данные для метода бисекции: левая граница интервала (a=0.5), правая граница интервала (b=1), погрешность вычисления корня уравнения (Eps).

З

ависимость числа итераций от Eps.

eps	итерации
0,1	2
0,01	5
0,001	8
0,0001	12
0,00001	15
0,000001	18

Обусловленность метода при разном delta при .

delta
0,1	0,8603335890	0,9	0,039666411	0,047011931
0,01	0,8603335890	0,86	0,000333589	0,004701193
0,001	0,8603335890	0,86	0,000333589	0,000470119
0,0001	0,8603335890	0,8603	3,3589E-05	4,70119E-05
0,00001	0,8603335890	0,86033	3,589E-06	4,70119E-06
0,000001	0,8603335890	0,860334	4,11E-07	4,70119E-07

4) Метод хорд.

Метод хорд основан на пропорциональном делении отрезка. Пусть найден отрезок (a, b), на котором функция меняет знак. Для определенности примем (a) > 0, (b) < 0. В методе хорд процесс итераций состоит в том, что в качестве приближений к значению корня уравнения принимаются значения c₀, c₁, . . . , c_n точек пересечения хорды с осью абсцисс, как это показано на рис.

Сначала решается уравнение хорды АВ:

Для нахождения точки пересечения ее с осью абсцисс (x = c₀, y = 0) используется уравнение:

Далее сравниваются знаки величин (a) и (с₀) и для рассматриваемого случая оказывается, что корень находится в интервале (a, c₀), так как (a)(с₀) < 0. Отрезок (c₀, b) отбрасывается. Следующая итерация состоит в определении нового приближения c₁ как точки пересечения хорды АВ₁ с осью абсцисс и т. д. Итерационный процесс продолжается до тех пор, пока значение (c_n) не станет по модулю меньше заданного числа .

Алгоритмы методов бисекции и хорд похожи, однако метод хорд в ряде случаев дает более быструю сходимость итерационного процесса, причем успех применения обоих гарантирован.

Исходные данные для метода хорд: левая граница интервала (a=0.5), правая граница интервала (b=1), погрешность вычисления корня уравнения (Eps).

З

ависимость числа итераций от Eps.

eps	итерации
0,1	1
0,01	1
0,001	2
0,0001	3
0,00001	4
0,000001	5

Обусловленность метода при разном delta при .

delta
0,1	0,8603335890	0,9	0,039666411	0,047011931
0,01	0,8603335890	0,86	0,000333589	0,004701193
0,001	0,8603335890	0,86	0,000333589	0,000470119
0,0001	0,8603335890	0,8603	3,3589E-05	4,70119E-05
0,00001	0,8603335890	0,86033	3,589E-06	4,70119E-06
0,000001	0,8603335890	0,860334	4,11E-07	4,70119E-07

5) Метод Ньютона.

В случае, когда известно хорошее начальное приближение решения уравнения , эффективным методом повышения точности является метод Ньютона. Он состоит в построении итерационной последовательности сходящейся к корню уравнения .

Метод Ньютона допускает простую геометрическую интерпретацию (рис). Если через точку с координатами провести касательную, то координата точки пересечения этой касательной с осью абсцисс будет очередным приближением x_{n +1} корня уравнения .

Для оценки погрешности n-го приближения корня предлагается пользоваться неравенством

где М₂ - наибольшее значение модуля второй производной на отрезке (a, b); m₁ - наименьшее значение модуля первой производной на отрезке (a, b).

Таким образом, если то Это означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т. е. процесс сходится очень быстро (имеет место квадратичная сходимость). Из указанного следует, что, при необходимости нахождения корня с точностью , итерационный процесс можно прекращать, когда соблюдается неравенство

Рассмотрим один шаг итераций. Если на (n-1)-м шаге очередное приближение x_{n -1} не удовлетворяет условию окончания процесса, то вычисляются величины и следующее приближение корня . При выполнении условия величина x_n принимается за приближенное значение корня с, вычисленное с точностью .

Для вычисления корня уравнения по методу Ньютона необходимо знать производную функции f(x):

Исходные данные для метода Ньютона: начальное приближение корня, удовлетворяющее условию (по графику видно, что этому условию удовлетворяет =1), погрешность вычисления корня (Eps).

З

ависимость числа итераций от Eps.

eps	итерации
0,1	1
0,01	2
0,001	3
0,0001	3
0,00001	3
0,000001	3

Обусловленность метода при разном delta при .

delta
0,1	0,8603335890	0,9	0,039666411	0,047011931
0,01	0,8603335890	0,86	0,000333589	0,004701193
0,001	0,8603335890	0,86	0,000333589	0,000470119
0,0001	0,8603335890	0,8603	3,3589E-05	4,70119E-05
0,00001	0,8603335890	0,86033	3,589E-06	4,70119E-06
0,000001	0,8603335890	0,860333	5,89E-07	4,70119E-07