Лабораторные работы 1 - 10 / Лаб раб 7

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

Кафедра МО ЭВМ

Вычислительная математика

Отчет

по выполнению лабораторной работы N7

Преподаватель: Щеголева Н.Л.

Студент группы 4351: Усенко А.В.

Санкт-Петербург, 2006

Постановка задачи

Требуется, используя квадратурные формулы прямоугольников, трапеций и Симпсона, вычислить значения заданного интеграла и, применив правило Рунге, найти наименьшее значение (наибольшее значение шага ), при котором каждая из указанных формул дает приближенное значение интеграла с погрешностью , не превышающей заданную.

Порядок выполнения работы.

1. Составить программы-функции для вычисления интегралов по формулам прямоугольников, трапеций и Симпсона.

2. Составить программу-функцию для вычисления подынтегральной функции.

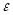3. Составить головную программу, содержащую оценку по Рунге погрешности каждой из перечисленных выше квадратурных формул, удваивающих до тех пор, пока погрешность не станет меньше , и осуществляющих печать результатов: значения интеграла и значения для каждой формулы. ( = 0.01; 0.001; 0.0001)

4. Провести вычисления по программе, добиваясь, чтобы результат удовлетворял требуемой точности.

5. Результаты работы оформить в виде краткого отчета, содержащего сравнительную оценку применяемых для вычисления формул.

Вариант задания – 16. Интеграл

Общие сведения

Повышения точности численного интегрирования добиваются путем применения составных формул. Для этого при нахождении определенного интеграла отрезок разбивают на четное число отрезков длины и на каждом из отрезков длины применяют соответствующую формулу. Таким образом получают составные формулы прямоугольников, трапеций и Симпсона.

На сетке , , , составные формулы имеют следующий вид:

формула прямоугольников

;

формула трапеций

;

формула Симпсона

,

где - остаточные члены. При приближенные значения интегралов для всех трех формул (в предположении отсутствия погрешностей округления) стремятся к точному значению интеграла [1,7,8].

Для практической оценки погрешности квадратурной можно использовать правило Рунге. Для этого проводят вычисления на сетках с шагом и , получают приближенные значения интеграла и и за окончательные значения интеграла принимают величины:

- для формулы прямоугольников;

- для формулы трапеций;

- для формулы Симпсона.

За погрешность приближенного значения интеграла для формул прямоугольников и трапеций тогда принимают величину , а для формулы Симпсона .

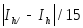Результаты вычислений

Метод прямоугольников

************ Rectangle ***************** Eps = 0.0100 N I(n) I(n/2) |I(n)-I(n/2)|/3 4 -0.084814 -0.080096 0.001573 ************ Rectangle ***************** Eps = 0.0010 N I(n) I(n/2) |I(n)-I(n/2)|/3 4 -0.084814 -0.080096 0.001573 8 -0.086013 -0.084814 0.000399 ************ Rectangle ***************** Eps = 0.0001 N I(n) I(n/2) |I(n)-I(n/2)|/3 4 -0.084814 -0.080096 0.001573 8 -0.086013 -0.084814 0.000399 16 -0.086313 -0.086013 0.000100 32 -0.086389 -0.086313 0.000025

Метод трапеций

************** Trapec ****************** Eps = 0.0100 N I(n) I(n/2) |I(n)-I(n/2)|/3 4 -0.089618 -0.099141 0.003174 ************** Trapec ****************** Eps = 0.0010 N I(n) I(n/2) |I(n)-I(n/2)|/3 4 -0.089618 -0.099141 0.003174 8 -0.087216 -0.089618 0.000801 ************** Trapec ****************** Eps = 0.0001 N I(n) I(n/2) |I(n)-I(n/2)|/3 4 -0.089618 -0.099141 0.003174 8 -0.087216 -0.089618 0.000801 16 -0.086614 -0.087216 0.000201 32 -0.086464 -0.086614 0.000050

Метод Симпсона

************** Simpson ***************** Eps = 0.0100 N I(n) I(n/2) |I(n)-I(n/2)|/3 4 -0.076183 0.000000 0.005079 ************** Simpson ***************** Eps = 0.0010 N I(n) I(n/2) |I(n)-I(n/2)|/3 4 -0.076183 0.000000 0.005079 8 -0.085149 -0.076183 0.000598 ************** Simpson ***************** Eps = 0.0001 N I(n) I(n/2) |I(n)-I(n/2)|/3 4 -0.076183 0.000000 0.005079 8 -0.085149 -0.076183 0.000598 16 -0.086256 -0.085149 0.000074

Вывод

Как видно из результатов вычислений, методы прямоугольников и трапеций имеют сходную точность, тогда как метод Симпсона оказался самым точным. Формулы прямоугольников и трапеций дают результат, сильно зависящий от величины шага h, что сказывается на точности вычисления определенного интеграла особенно в тех случаях, когда функция имеет немонотонный характер. При использовании вместо отрезков прямых, заменяющих криволинейные фрагменты графика функции f(x), фрагментов парабол, проводимых через три соседних точки графика(подобная геометрическая интерпретация лежит в основе метода Симпсона для вычисления определенного интеграла) точность вычислений становится заметно выше даже при большей величине шага h.