Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

Вычислительная математика

Файл:

Лабораторные работы 1 - 10 / Лаб раб 4

.doc

Скачиваний:

Добавлен:

01.05.2014

Размер:

154.11 Кб

Скачать

☆

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

Кафедра МО ЭВМ

Вычислительная математика

Отчет

по выполнению лабораторной работы N4

Преподаватель: Щеголева Н.Л.

Студент группы 4351: Усенко А.В.

Санкт-Петербург, 2006

Постановка задачи

Необходимо исследовать обусловленность задачи нахождения корня уравнения для нелинейной функции (Вариант 16). Значение корня х вычисляется с помощью метода хорд. Функция вычисляется приближенно, с точностью Delta, варьируемой в пределах от 0.1 до 0.000001. Корень уравнения вычисляется с заданной точностью Eps, варьируемой от 0.1 до 0.000001. Вычисления провести для различных наборов параметров Delta, Eps. Теоретически и экспериментально исследовать скорость сходимости и обусловленность метода.

Общие сведения

Пусть найден отрезок [a, b], на котором функция меняет знак. Для определенности положим (a)>0, (b)<0. В методе хорд процесс итераций состоит в том, что в качестве приближений к корню уравнения принимаются значения x₀, x₁, . . . точек пересечения хорды с осью абсцисс, как это показано на рис.1.

Сначала находится уравнение хорды АВ:

Для точки пересечения ее с осью абсцисс (x=c₀, y=0) получается уравнение

Далее сравниваются знаки величин (a) и (x₀) и для рассматриваемого случая оказывается, что корень находится в интервале (a, x₀), так как (a)(x₀)<0. Отрезок [x₀,b] отбрасывается. Следующая итерации состоит в определении нового приближения c₁ как точки пересечения хорды АВ₁ с осью абсцисс и т.д. Итерационный процесс продолжается до тех пор, пока значение (x_n) не станет по модулю меньше заданного числа .

Анализ задачи

По графику функции можно произвести отделение корня.

График функции:

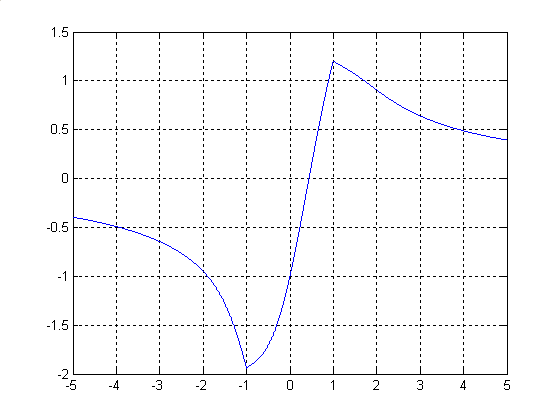
Возьмем начальные границы интервала [0;1].

Теоретическое абсолютное число обусловленности . Погрешность вычисления корня определяется по формуле: . Если практическая погрешность вычисления корня больше или равна теоретический, то задача хорошо обусловлена, иначе – плохо обусловлена.

Функция:

Производная:

Исходный текст программы

Файл: Lr_4.cpp

Автор: Усенко А.В.

Ред. 1.0 06.10.06

#include <iostream.h>

#include <math.h>

#include <conio.h>

#include <fstream.h>

#include "methods.h"

// Global variables

double F(double); // Function

double F1(double); // Derivative

ofstream f_out; // Output data file

char out_path[11]="output.txt"; // Output file name

double delta=0.1, // function calculating error

eps=0.1, // output data error

eps_theor=0; // Theoretical eps value

double a=0,b=1; // interval borders

void main()

{

clrscr();

double func_val, // value of function

x; // value of root

int n; // number of iterations

// file opening

f_out.open(out_path);

if (f_out.fail())

{

cout<<"Impossible to open output file!"<<endl;

exit(1);

}

f_out.setf(ios::fixed);

f_out.setf(ios::showpoint);

/* Calculating & table printing */

delta=0.1;

for (int j=1; j<=6; j++)

{

f_out.precision(j);

f_out<<"Delta = "<<delta<<endl;

eps=0.1;

f_out<<"Eps\t\t"<<"X\t\t"<<"F(x)\t\t"<<"N\t"<<"Eps_Theor\t"<<"Condit\n";

for (int i=1; i<=6; i++)

{

f_out.precision(i);

x=HORDA(a,b,eps,n);

f_out<<eps<<"\t"; if (i<6) {f_out<<"\t";};

f_out<<x<<"\t"; if (i<6) {f_out<<"\t";};

f_out.precision(j);

f_out<<F(x)<<"\t"; if ( (j<6) && !((j==5)&&(F(x)<0)) ) {f_out<<"\t";};

f_out<<n<<"\t";

eps_theor=delta/fabs(F1(x));

f_out.precision(6);

f_out<<eps_theor<<"\t";

if (eps>=eps_theor) {f_out<<"good\n";}

else {f_out<<"bad\n";}

eps = eps/10;

}

f_out<<endl<<endl;

delta = delta/10;

}

f_out.close();

cout<<"Program finished. Press <Enter>...";

getch();

return;

}

// Function definition

double F(double x)

{

extern double delta;

double s;

s = asin(2*x/(1+x*x))-exp(-x*x);

return Round(s,delta);

}

// Derivative definition

double F1(double x)

{

double s;

s=(2-4*x*x)/((1+x*x)*sqrt(1-4*x*x/pow((1+x*x),2))) + 2*x*exp(-x*x);

return s;

}

Результаты вычислений

В следующей таблице представлены результаты вычисления корня при различных комбинациях параметров Eps, Delta. Также представлены сравнения теоретических и экспериментальных значений абсолютного числа обусловленности.

Delta = 0.1

Eps X F(x) F'(x) N Eps_Theor Condit

0.1 0.5 0.0 2.2 1 0.045455 good

0.01 0.45 0.0 2.2 1 0.045455 bad

0.001 0.455 0.0 2.2 1 0.045455 bad

0.0001 0.4545 0.0 2.2 1 0.045455 bad

0.00001 0.45455 0.0 2.2 1 0.045455 bad

0.000001 0.454545 0.0 2.2 1 0.045455 bad

Delta = 0.01

Eps X F(x) F'(x) N Eps_Theor Condit

0.1 0.5 0.04 2.22 1 0.004505 good

0.01 0.44 0.00 2.25 2 0.004444 good

0.001 0.437 0.00 2.25 2 0.004444 bad

0.0001 0.4371 0.00 2.25 2 0.004444 bad

0.00001 0.43706 0.00 2.25 2 0.004444 bad

0.000001 0.437063 0.00 2.25 2 0.004444 bad

Delta = 0.001

Eps X F(x) F'(x) N Eps_Theor Condit

0.1 0.5 0.038 2.220 1 0.000450 good

0.01 0.44 -0.001 2.249 2 0.000445 good

0.001 0.438 0.000 2.249 3 0.000445 good

0.0001 0.4377 0.000 2.249 3 0.000445 bad

0.00001 0.43773 0.000 2.249 3 0.000445 bad

0.000001 0.437735 0.000 2.249 3 0.000445 bad

Delta = 0.0001

Eps X F(x) F'(x) N Eps_Theor Condit

0.1 0.5 0.0385 2.2197 1 0.000045 good

0.01 0.44 -0.0019 2.2498 2 0.000044 good

0.001 0.438 0.0000 2.2485 3 0.000044 good

0.0001 0.4379 0.0000 2.2485 3 0.000044 good

0.00001 0.43791 0.0000 2.2485 3 0.000044 bad

0.000001 0.437909 0.0000 2.2485 3 0.000044 bad

Delta = 0.00001

Eps X F(x) F'(x) N Eps_Theor Condit

0.1 0.5 0.03848 2.21972 1 0.000005 good

0.01 0.44 -0.00188 2.24977 2 0.000004 good

0.001 0.438 0.00000 2.24847 3 0.000004 good

0.0001 0.4379 0.00000 2.24847 3 0.000004 good

0.00001 0.43791 0.00000 2.24847 3 0.000004 good

0.000001 0.437906 0.00000 2.24847 3 0.000004 bad

Delta = 0.000001

Eps X F(x) F'(x) N Eps_Theor Condit

0.1 0.5 0.038477 2.219724 1 0.000000 good

0.01 0.44 -0.001878 2.249764 2 0.000000 good

0.001 0.438 0.000001 2.248467 3 0.000000 good

0.0001 0.4379 0.000001 2.248467 3 0.000000 good

0.00001 0.43791 0.000001 2.248467 3 0.000000 good

0.000001 0.437907 0.000000 2.248467 4 0.000000 good

Далее представлена таблица, иллюстрирующая сходимость метода хорд.

Delta 0.100000000

Eps 0.100000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

/------------------------------/

Delta 0.100000000

Eps 0.010000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

/------------------------------/

Delta 0.100000000

Eps 0.001000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

/------------------------------/

Delta 0.100000000

Eps 0.000100000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

/------------------------------/

Delta 0.100000000

Eps 0.000010000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

/------------------------------/

Delta 0.100000000

Eps 0.000001000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

/------------------------------/

Delta 0.010000000

Eps 0.100000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

/------------------------------/

Delta 0.010000000

Eps 0.010000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

2 0.454545455 0.437062937 0.017482517 0.050699701

/------------------------------/

Delta 0.010000000

Eps 0.001000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

2 0.454545455 0.437062937 0.017482517 0.050699701

/------------------------------/

Delta 0.010000000

Eps 0.000100000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

2 0.454545455 0.437062937 0.017482517 0.050699701

/------------------------------/

Delta 0.010000000

Eps 0.000010000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

2 0.454545455 0.437062937 0.017482517 0.050699701

/------------------------------/

Delta 0.010000000

Eps 0.000001000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.454545455 0.545454545 0.029601711

2 0.454545455 0.437062937 0.017482517 0.050699701

/------------------------------/

Delta 0.001000000

Eps 0.100000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453926464 0.546073536 0.028500488

/------------------------------/

Delta 0.001000000

Eps 0.010000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453926464 0.546073536 0.028500488

2 0.453926464 0.437308732 0.016617732 0.037315605

/------------------------------/

Delta 0.001000000

Eps 0.001000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453926464 0.546073536 0.028500488

2 0.453926464 0.437308732 0.016617732 0.037315605

3 0.437308732 0.437734828 0.000426096 0.287219484

/------------------------------/

Delta 0.001000000

Eps 0.000100000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453926464 0.546073536 0.028500488

2 0.453926464 0.437308732 0.016617732 0.037315605

3 0.437308732 0.437734828 0.000426096 0.287219484

/------------------------------/

Delta 0.001000000

Eps 0.000010000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453926464 0.546073536 0.028500488

2 0.453926464 0.437308732 0.016617732 0.037315605

3 0.437308732 0.437734828 0.000426096 0.287219484

/------------------------------/

Delta 0.001000000

Eps 0.000001000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453926464 0.546073536 0.028500488

2 0.453926464 0.437308732 0.016617732 0.037315605

3 0.437308732 0.437734828 0.000426096 0.287219484

/------------------------------/

Delta 0.000100000

Eps 0.100000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453947070 0.546052930 0.028537147

/------------------------------/

Delta 0.000100000

Eps 0.010000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453947070 0.546052930 0.028537147

2 0.453947070 0.437118026 0.016829044 0.049156687

/------------------------------/

Delta 0.000100000

Eps 0.001000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453947070 0.546052930 0.028537147

2 0.453947070 0.437118026 0.016829044 0.049156687

3 0.437118026 0.437909491 0.000791465 0.003760236

/------------------------------/

Delta 0.000100000

Eps 0.000100000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453947070 0.546052930 0.028537147

2 0.453947070 0.437118026 0.016829044 0.049156687

3 0.437118026 0.437909491 0.000791465 0.003760236

/------------------------------/

Delta 0.000100000

Eps 0.000010000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453947070 0.546052930 0.028537147

2 0.453947070 0.437118026 0.016829044 0.049156687

3 0.437118026 0.437909491 0.000791465 0.003760236

/------------------------------/

Delta 0.000100000

Eps 0.000001000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453947070 0.546052930 0.028537147

2 0.453947070 0.437118026 0.016829044 0.049156687

3 0.437118026 0.437909491 0.000791465 0.003760236

/------------------------------/

Delta 0.000010000

Eps 0.100000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453942948 0.546057052 0.028529815

/------------------------------/

Delta 0.000010000

Eps 0.010000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453942948 0.546057052 0.028529815

2 0.453942948 0.437122476 0.016820473 0.048891838

/------------------------------/

Delta 0.000010000

Eps 0.001000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453942948 0.546057052 0.028529815

2 0.453942948 0.437122476 0.016820473 0.048891838

3 0.437122476 0.437905986 0.000783511 0.000688163

/------------------------------/

Delta 0.000010000

Eps 0.000100000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453942948 0.546057052 0.028529815

2 0.453942948 0.437122476 0.016820473 0.048891838

3 0.437122476 0.437905986 0.000783511 0.000688163

/------------------------------/

Delta 0.000010000

Eps 0.000010000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453942948 0.546057052 0.028529815

2 0.453942948 0.437122476 0.016820473 0.048891838

3 0.437122476 0.437905986 0.000783511 0.000688163

/------------------------------/

Delta 0.000010000

Eps 0.000001000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453942948 0.546057052 0.028529815

2 0.453942948 0.437122476 0.016820473 0.048891838

3 0.437122476 0.437905986 0.000783511 0.000688163

/------------------------------/

Delta 0.000001000

Eps 0.100000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453943567 0.546056433 0.028530915

/------------------------------/

Delta 0.000001000

Eps 0.010000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453943567 0.546056433 0.028530915

2 0.453943567 0.437124334 0.016819233 0.048774093

/------------------------------/

Delta 0.000001000

Eps 0.001000000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453943567 0.546056433 0.028530915

2 0.453943567 0.437124334 0.016819233 0.048774093

3 0.437124334 0.437907050 0.000782716 0.000670251

/------------------------------/

Delta 0.000001000

Eps 0.000100000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453943567 0.546056433 0.028530915

2 0.453943567 0.437124334 0.016819233 0.048774093

3 0.437124334 0.437907050 0.000782716 0.000670251

/------------------------------/

Delta 0.000001000

Eps 0.000010000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453943567 0.546056433 0.028530915

2 0.453943567 0.437124334 0.016819233 0.048774093

3 0.437124334 0.437907050 0.000782716 0.000670251

/------------------------------/

Delta 0.000001000

Eps 0.000001000

N X(i-1) X(i) |X(i)-X(i-1)| |(X(i)-X)/(X(i-1)-X)|

1 1.000000000 0.453943567 0.546056433 0.028530915

2 0.453943567 0.437124334 0.016819233 0.048774093

3 0.437124334 0.437907050 0.000782716 0.000670251

4 0.437907050 0.437906633 0.000000417 0.205440400

/------------------------------/

Теоретически метод хорд сходится линейно, что и можно наблюдать в таблице.

, где c = const ≈ , 0<c<1. В нашем случае c не превышает 0.3. В общем случае константа с зависит от вида функции (значения первой производной в σ-окрестности корня).

Вывод

Как видно из результатов вычислений, задача хорошо обусловлена в случаях, когда требуемая погрешность результата меньше или равна погрешности входных данных. Необходимое количество итераций повышается с увеличением точности входных данных. Для достижения тех же результатов методу хорд потребовалось намного меньше итераций, чем методу бисекции. При малых погрешностях число итераций по сравнению с методом бисекции сократилось в 5 раз. Экспериментальная сходимость метода хорд, как и теоретическая, имеет линейный характер.

Соседние файлы в папке Лабораторные работы 1 - 10

#
01.05.2014166.91 Кб33Лаб раб 10.doc
#
01.05.201486.02 Кб33Лаб раб 2.doc
#
01.05.201434.3 Кб27Лаб раб 2.xls
#
01.05.201498.82 Кб29Лаб раб 3.doc
#
01.05.201435.84 Кб22Лаб раб 3.xls
#
01.05.2014154.11 Кб29Лаб раб 4.doc
#
01.05.2014392.19 Кб30Лаб раб 5.doc
#
01.05.201432.77 Кб22Лаб раб 5.xls
#
01.05.2014143.87 Кб31Лаб раб 6.doc
#
01.05.2014101.89 Кб29Лаб раб 7.doc
#
01.05.201477.82 Кб29Лаб раб 8.doc