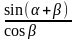- •2 Разработка компрессора
- •2.1 Расчёт основных параметров компрессора
- •2.2.1 Разработка поршня
- •2.2.2 Разработка цилиндров
- •2.2.3 Разработка шатуна
- •2.2.4 Расчет коленчатого вала
- •2.3 Расчет газового тракта компрессора.
- •3 Динамический расчет компрессора.
- •4.1 Уравновешивание
- •4.2Расчет смазки подшипников скольжения поршневого компрессора
- •5 Разработка конденсатора.
- •5.1Испарительный
- •5.2 Кожухотрубный горизонтальный
- •5.3 Кожухотрубный вертикальный
- •5.4 Оросительный
3 Динамический расчет компрессора.
Динамический расчет проводят для определения сил, действующих на кривошипно-шатунный механизм компрессора в зависимости от угла поворота коленчатого вала.
Результаты динамического расчета служат основой для определения необходимого махового момента маховика, расчета противовесов, определения неуравновешенных сил, действующих на фундамент, прочностных расчетов деталей компрессора, расчета подшипников на износ, а также для проектирования системы смазки.
Динамический расчет включает в себя:
построение индикаторной диаграммы;
построение диаграммы суммарной силы, действующей по оси цилиндра;
построение диаграммы тангенциальных сил;
построение диаграммы радиальных сил
а. Построение индикаторной диаграммы.
Известны аналитический и графический методы построения расчетных индикаторных диаграмм.
Аналитический метод построения линий сжатия и обратного расширения основан на использовании уравнения политропы yxn=const, где x и y – коэффициенты точек политроп сжатия и обратного расширения; n – показатель политропы. Этот метод обычно используют для рабочих веществ, параметры состояния которых значительно отклоняются от законов для идеального газа.
Графический метод построения по способу Брауэра основан на уравнении (tgφ+1)n= tgψ+1. устанавливающем cвязь между координатами определенных политропы и разностями координат этих точек.
Индикаторная диаграмма строится в системе координат S, PyFп. По оси абсцисс в принятом масштабе откладываем значения мертвого пространства:
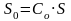 м
и хода поршня S.
По оси ординат в масштабе откладываем
силы от давления пара на поршень.
м
и хода поршня S.
По оси ординат в масштабе откладываем
силы от давления пара на поршень.
Силы от давлений:
П=Р* Fп (3.1)
П - силы от давления пара на поршень, Н;
Fп - площадь поршня, м2;
Р - давление газа на поршень, Па.
Сила от давления всасывания:
Пвс = Рвс ∙ Fп, Н (3.2)
Сила от давления кипения:
По = Ро ∙ Fп, Н (3.3)
Сила от давления нагнетания :
Пн = Рн ∙ Fп, Н (3.4)
Сила от давления конденсации:
Пк = Рк ∙Fп, Н (3.5)
При построении политроп сжатия и обратного расширения необходимо провести вспомогательный луч из начала координат под произвольным углом φ к оси абсцисс (рекомендуется φ=10÷15º) и задаться значениями показателей политроп сжатия nc и обратного расширения nр.
Для хладоновых компрессоров значения политроп сжатия nc и обратного расширения nр, принимают:
nc=1,05÷1,1
nр=1,0 ÷1,05
Для аммиачных компрессоров значения политроп сжатия nc и обратного расширения nр, принимают:
nc=1,2÷1,25
nр=1,1÷1,15
Для построения точек политропы сжатия используются вспомогательные лучи, проведенные из начала координат под углом ψс к оси ординат, а для политропы расширения – луч, проведенный под углом ψр.
Угол вспомогательного луча ψс для политропы сжатия находим из уравнения
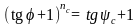 ;
(3.6)
;
(3.6)
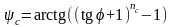 (3.7)
(3.7)
Для политропы расширения:
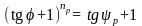 ;
(3.8)
;
(3.8)
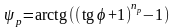 (3.9)
(3.9)
Порядок
построения следующий: из точки
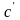 с координатами (S+S0);
Р0·F0
опускают перпендикуляр
h
на ось абсцисс, из полученной точки под
углом 45º к оси абсцисс проводят линию
до пересечения с вспомогательным лучом
(φ), Из точки g
надо восстановить перпендикуляр. Затем
из точки
проводят горизонталь до пересечения с
лучом (ψс).
Из полученной точки под углом 45º к оси
ординат проводят прямую до пересечения
с осью ординат. Из полученной точки
проводят горизонталь до пересечения в
точке е с перпендикуляром, восстановленным
из точки g.
Точка е лежит на политропе сжатия.
с координатами (S+S0);
Р0·F0
опускают перпендикуляр
h
на ось абсцисс, из полученной точки под
углом 45º к оси абсцисс проводят линию
до пересечения с вспомогательным лучом
(φ), Из точки g
надо восстановить перпендикуляр. Затем
из точки
проводят горизонталь до пересечения с
лучом (ψс).
Из полученной точки под углом 45º к оси
ординат проводят прямую до пересечения
с осью ординат. Из полученной точки
проводят горизонталь до пересечения в
точке е с перпендикуляром, восстановленным
из точки g.
Точка е лежит на политропе сжатия.
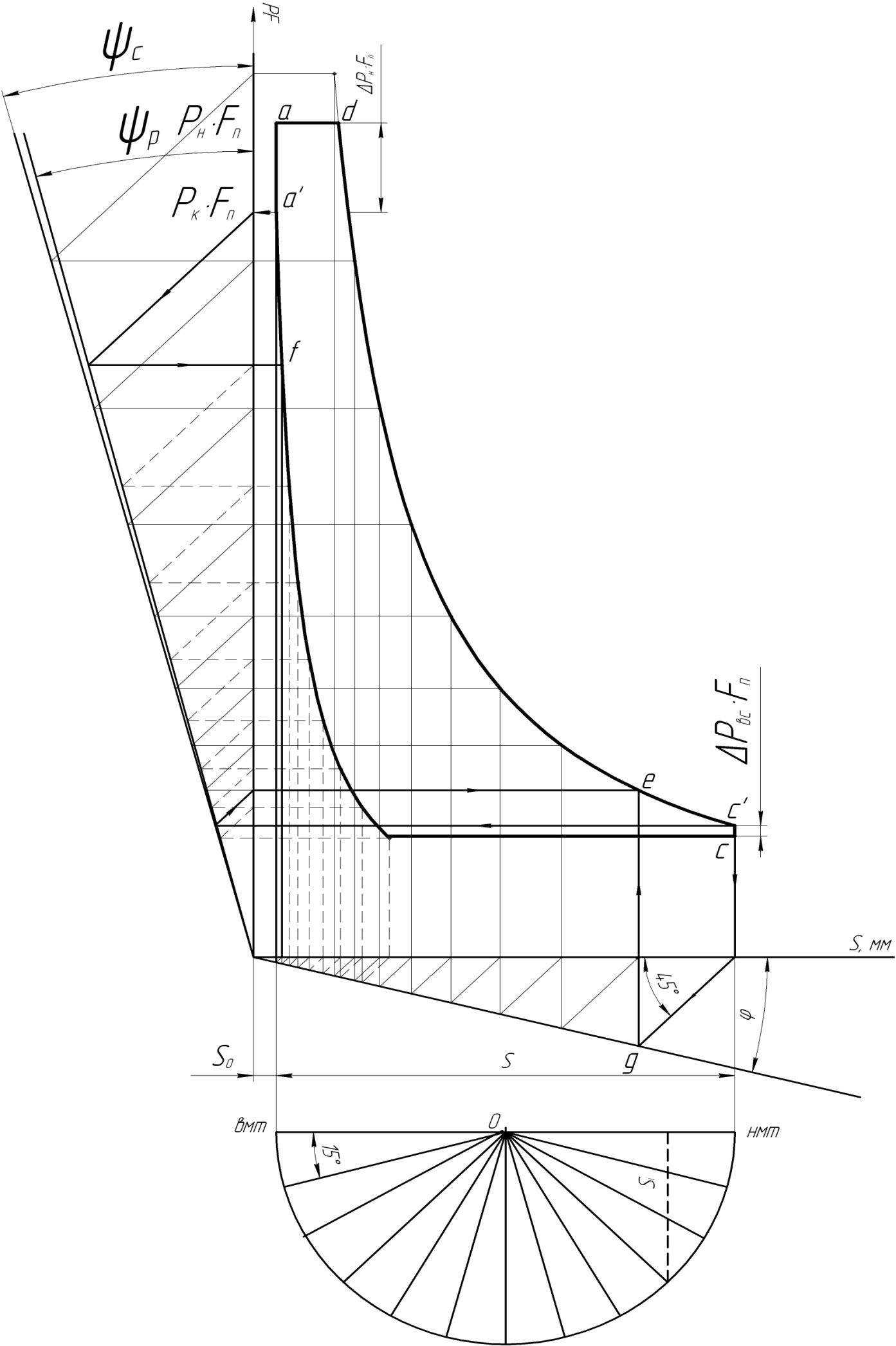
Рисунок 3 Индикаторная диаграмма
Последовательное повторение приведенного построения позволит получить политропу сжатия.
Порядок
построения политропы расширения
аналогичен. Начинают построения из
точки
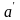 с координатами S0;Рк·Fп
опускают перпендикуляр на ось ординат,
из полученной точки под углом 45º к оси
ординат проводят линию до пересечения
с лучом (ψр).
Из этой точки надо восстановить
перпендикуляр к оси ординат. Затем из
точки
проводят вертикаль до пересечения с
лучом (φ). Из полученной точки под углом
45º к оси абсцисс проводят прямую до
пересечения с осью абсцисс. Из полученной
точки проводят вертикаль до пересечения
в точке f
с перпендикуляром, восстановленным от
луча (ψр).
Точка f
лежит на политропе расширения.
с координатами S0;Рк·Fп
опускают перпендикуляр на ось ординат,
из полученной точки под углом 45º к оси
ординат проводят линию до пересечения
с лучом (ψр).
Из этой точки надо восстановить
перпендикуляр к оси ординат. Затем из
точки
проводят вертикаль до пересечения с
лучом (φ). Из полученной точки под углом
45º к оси абсцисс проводят прямую до
пересечения с осью абсцисс. Из полученной
точки проводят вертикаль до пересечения
в точке f
с перпендикуляром, восстановленным от
луча (ψр).
Точка f
лежит на политропе расширения.
Последовательное повторение приведенного построения позволит получить политропу расширения.
б. Построение диаграммы суммарной силы, действующей по оси цилиндра.
Диаграмма суммарной силы получается в результате графического суммирования газовой силы, силы инерции от масс, движущихся возвратно-поступательно, и силы трения поступательно движущихся частей.
Чтобы
построить линию газовой силы на диаграмме
суммарной силы надо развернуть
индикаторную диаграмму. Координату
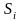 на индикаторной диаграмме, соответствующую
некоторому углу поворота вала
на индикаторной диаграмме, соответствующую
некоторому углу поворота вала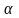 ,
находят следующим образом.
,
находят следующим образом.
На
ходе поршня
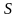 как на диаметре строят полуокружность.
Из центра окружности
как на диаметре строят полуокружность.
Из центра окружности
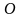 ,
под углом
к
оси
проводится
прямая до пересечения с полуокружностью,
а из точки пересечения – параллельная
оси ординат до пересечения с осью
.
Точка пересечения соответствует ходу
поршня
.
,
под углом
к
оси
проводится
прямая до пересечения с полуокружностью,
а из точки пересечения – параллельная
оси ординат до пересечения с осью
.
Точка пересечения соответствует ходу
поршня
.
При построении диаграммы суммарной силы по оси абсцисс откладывается двойной ход поршня S. Левая половина диаграммы показывает силы при ходе поршня к валу (=0180), правая - при обратном ходе (=180360). Положения поршня, соответствующее углу поворота кривошипа , находится при помощи построения по способу Брикса. Для этого от центра О окружности с диаметром, равным ходу поршня в масштабе длин, в сторону точки, соответствующей 180,откладывается отрезок:
ОО'
=
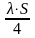 ,
м (3.10)
,
м (3.10)
где λ – отношении радиуса кривошипа к длине шатуна:
λ = r/Lш = 0,5*S/Lш (3.11)
r – радиус кривошипа, м;
Lш – длинна шатуна, м;
S – ход поршня, м.
Считывая значения газовой силы, соответствующие последовательным углам поворота вала, переносят эти значения на диаграмму суммарной силы. На эту же диаграмму наносятся силы инерции и силы трения.
Суммарная сила, действующая в направлении оси цилиндра:
Рi= Пi+Ini+Rтpi, Н (3.12)
где Пi – сила от давления пара на поршень;
Rтpi - cила трения;
I ni - сила инерции;
Ini = In1+In2= -mn∙r∙ω2∙ cos a – mn∙r∙ ω2∙λ∙cos2a (3.13)
где - mn - масса поступательно движущихся частей
mn= mпор+1/3∙mшат ,кг (3.14)
где – mпор масса поршня;
mшат - масса шатуна.
Расчет массы поршня:
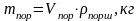 ,
(3.15)
,
(3.15)
где
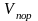 - объем поршня;
- объем поршня;
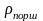 -
плотность материала из которого
изготовлен поршень;,
-
плотность материала из которого
изготовлен поршень;,
 .
(3.16)
.
(3.16)
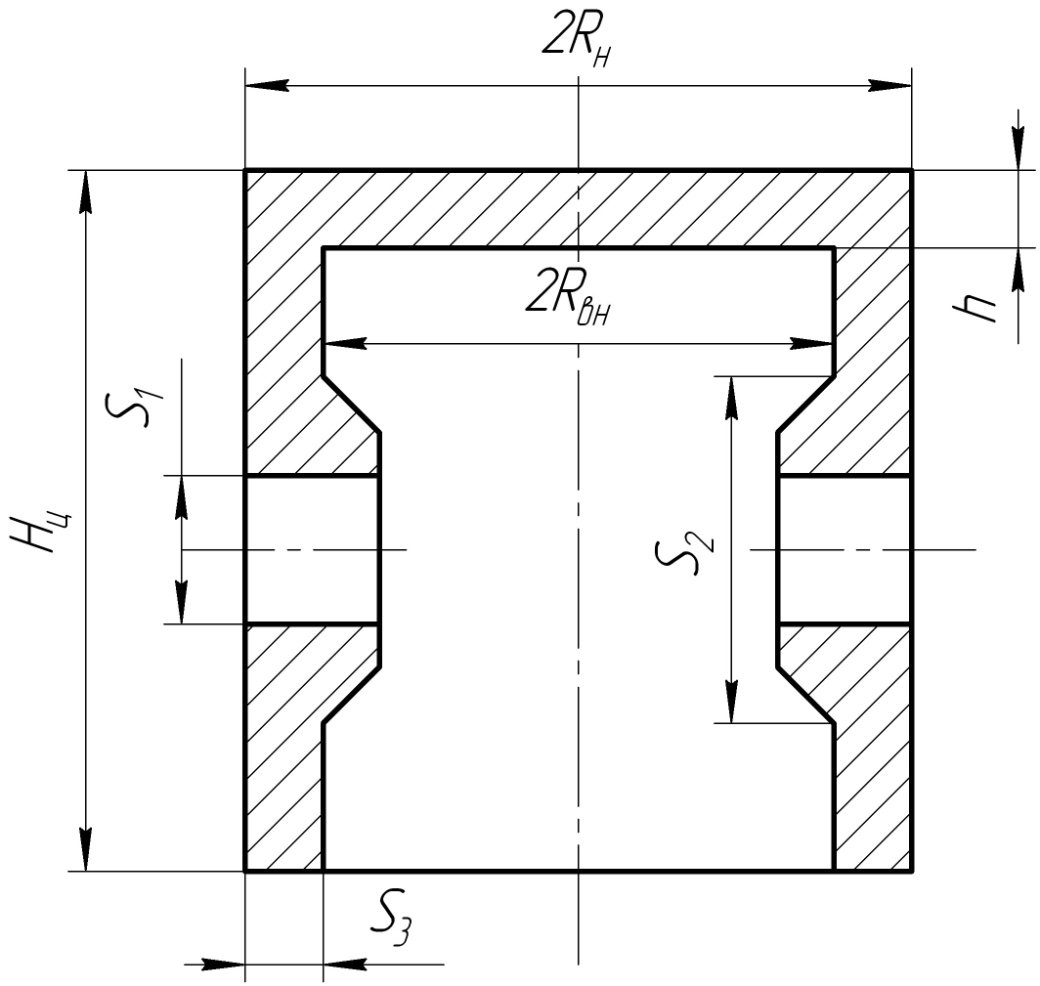
Рисунок 4 Чертеж поршня
Объем цилиндра без внутренней части:
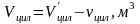 ,
(3.17)
,
(3.17)
где
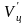 - объем цилиндра;
- объем цилиндра;
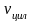 -
объем внутренней части.
-
объем внутренней части.
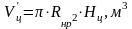 ,
(3.18)
,
(3.18)
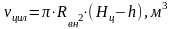 ,
(3.19)
,
(3.19)
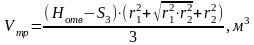 ,
(3.20)
,
(3.20)
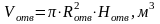 ,
(3.21)
,
(3.21)
Расчет массы шатуна:
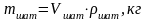 ,
(3.22)
,
(3.22)
где
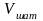 - объем шатуна;
- объем шатуна;
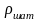 -
плотность материала из которого
изготовлен шатун, кг/м3,
-
плотность материала из которого
изготовлен шатун, кг/м3,
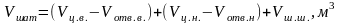 ,
(3.23)
,
(3.23)
где
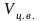 - объем верхнего цилиндра;
- объем верхнего цилиндра;
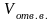 -
объем верхнего отверстия;
-
объем верхнего отверстия;
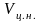 -
объем нижнего цилиндра;
-
объем нижнего цилиндра;
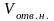 -
объем нижнего цилиндра;
-
объем нижнего цилиндра;
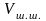 -
объем шатунной шейки.
-
объем шатунной шейки.
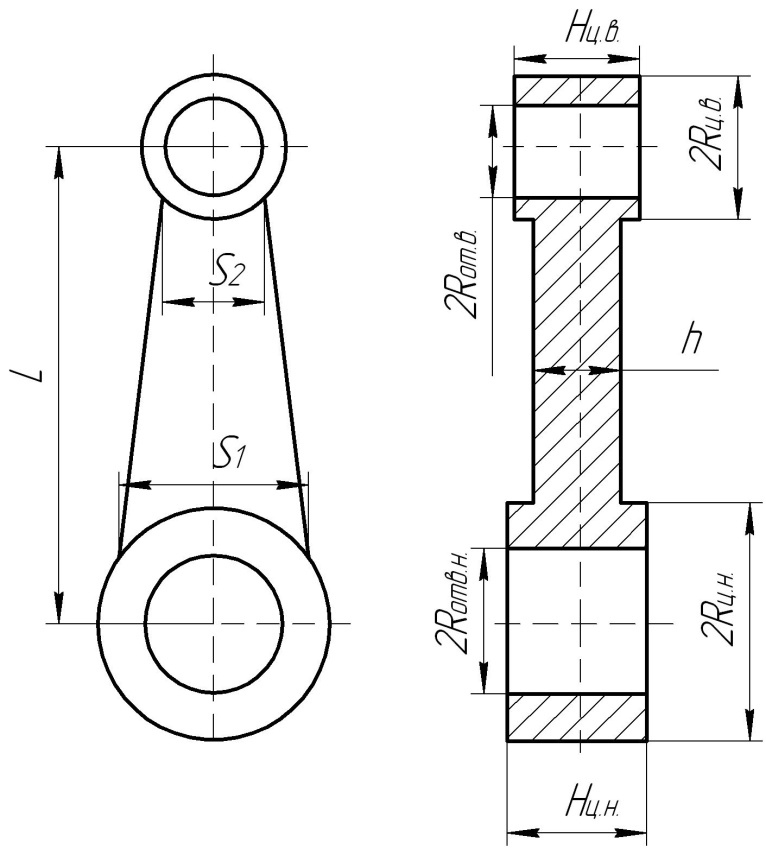
Рисунок 5 Чертеж шатуна
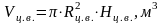 ,
(3.24)
,
(3.24)
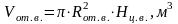 ,
(3.25)
,
(3.25)
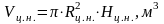 ,
(3.26)
,
(3.26)
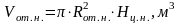 ,
(3.27)
,
(3.27)
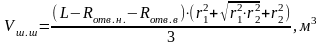 ,
(3.28)
,
(3.28)
Силу трения поступательно движущихся частей полагают постоянной и меняющей знак в мертвых точках.
Rтрi=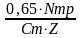 ,Н (3.29)
,Н (3.29)
где – N mp - мощность трения:
N mp = Pi mp∙Vт ,кВт (3.30)
где – Pi m Па - давление трения.
Сила инерции первого порядка:
In1= - mn∙r∙ω2∙cos a. ,Н (3.31)
Сила инерции второго порядка:
In2= -mn∙r∙ω2∙λ∙cos2a, Н (3.32)
где r ,м– половина хода поршня:
ω - угловая скорость вращения;
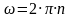 (3.33)
(3.33)
где
n
– частота вращения вала,
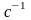 .
.
Результаты расчета сводятся в таблицу.
Таблица 4 Результаты расчета
α,º |
cosα |
λ·cos2α |
|
|
|
П,Н |
Р,Н |
0 |
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
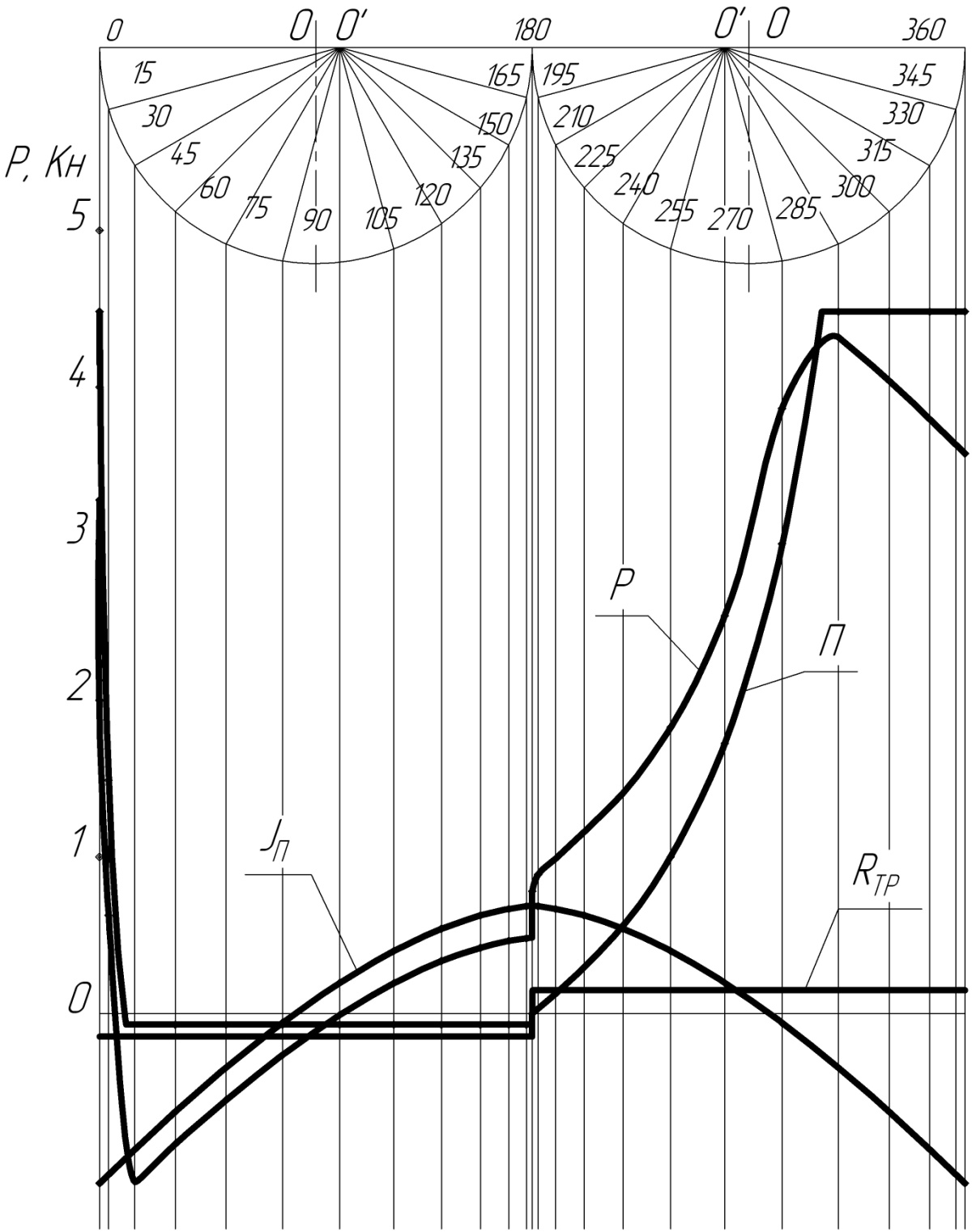
Рисунок 6 Диаграмма суммарной силы
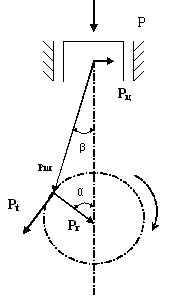
в.Построение диаграмм тангенциальных и радиальных сил.
Тангенциальную силу для одного цилиндра рассчитываем на основе полученных выше значений суммарной свободной силы для 24 положений кривошипа.
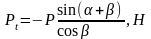 (3.34)
(3.34)
Значения функций Sin(α+β)/cos β = f (α;λ), могут быть определены с помощью уравнений:
sin β=λ·sin α (3.35)
cos
β=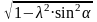 . (3.36)
. (3.36)
Влияние силы трения вращающихся частей Rвр компрессора учитывают смещением начала отсчета ординат суммарной кривой тангенциальных сил от оси абсцисс на отрезок ОО', равный в масштабе сил диаграммы значению силы Rвр :
Rвр =0,35 Nтр/Cm (3.37)
Среднее значение суммарной тангенциальной силы определяем планиметрированием площади под кривой ∑Рt + Rвр. Частное от деления полученной площади на длину диаграммы (0-360) дает ординату Ptср. Менее точно среднее значение суммарной тангенциальной силы Ptср находят делением суммы 24 ординат, взятых на диаграмме, на их количество.
Кривая
суммарных тангенциальных сил является
кривой моментов, противодействующих
вращению вала:
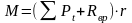 .
Площадки f1
и f2
между
прямой Ptср
и кривой суммарной тангенциальной силы
характеризуют неравномерность нагрузки
на двигатель. Площадки под прямой Ptср
принято
считать отрицательными, над прямой –
положительными.
.
Площадки f1
и f2
между
прямой Ptср
и кривой суммарной тангенциальной силы
характеризуют неравномерность нагрузки
на двигатель. Площадки под прямой Ptср
принято
считать отрицательными, над прямой –
положительными.
При точном определении Ptср алгебраическая сумма всех площадок должна равняться нулю. По наибольшей площади f1 или f2 рассчитывается маховик.
В координатах Рt, α строим кривую тангенциальных сил для одного цилиндра. Затем, последовательно смещая по углу поворота кривошипа кривую тангенциальных сил одного цилиндра на угол развала между рядами компрессора, строим кривые тангенциальных сил для всех цилиндров Рt1 - Рti. Кривую суммарной тангенциальной силы получаем сложением ординат всех кривых тангенциальных сил.
Результаты расчета тангенциальных сил сводятся в таблицу
Таблица 5 результаты расчета тангенциальных сил
α,º |
Р,Н |
|
Рt,Н |
α,º |
Р,Н |
|
Рt,Н |
0 |
|
|
|
180 |
|
|
|
15 |
|
|
|
195 |
|
|
|
… |
|
|
|
… |
|
|
|
180 |
|
|
|
360 |
|
|
|
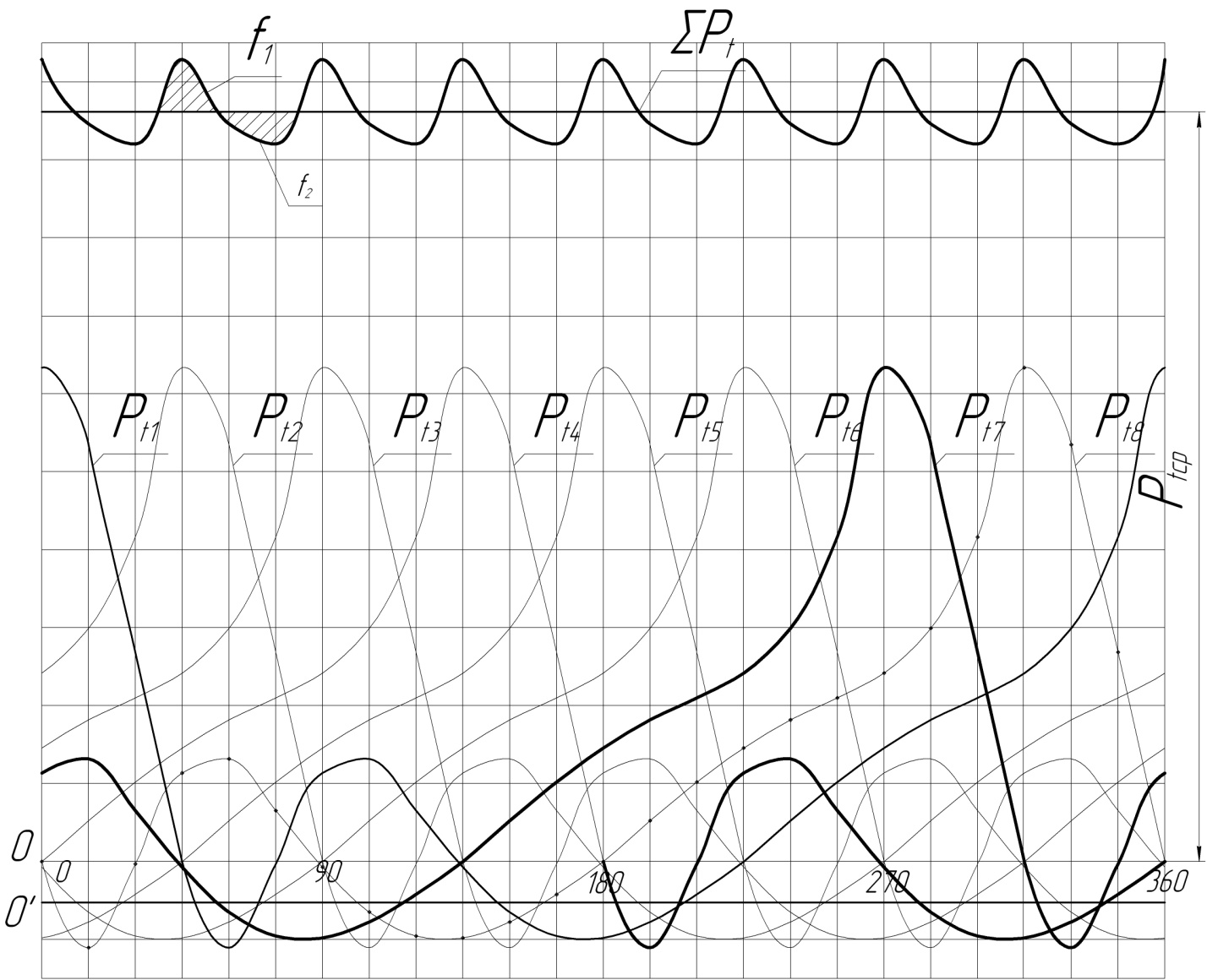
Рисунок 7 Диаграмма тангенциальных сил
Диаграмма радиальных сил строится в координатах Рr ,α.
Pr=
P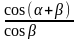 ,Н,
(3.38)
,Н,
(3.38)
Pr – радиальная сила.
Значения функций cos (α+β)/cos β = f (α;λ), могут быть определены с помощью уравнений:
sin β=λ·sin α (3.39)
cos β= . (3.40)
В радиальном направлении на кривошип кроме силы Рr действуют постоянные по величине силы инерции I ш.ш. от массы части шатунной шейки, приходящейся на один шатун, и от вращающейся части шатуна I ш.вр.:
Iш.ш.= mш.ш.∙r∙ω2 (3.41)
mш.ш. = (π∙d2∙lш.ш.∙ρ)/(4∙i), (кг) (3.42)
где m ш.ш.- масса шатунной шейки;
lшш ,м - длина шатунной шейки;
lшш=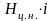 ; (3.43)
; (3.43)
dш.ш. ,м - диаметр шатунной шейки;
i - число шатунов на одной шатунной шейке;
ρ ,кг/м3- плотность материала коленчатого вала;
Сила инерции от вращающейся части шатуна I ш.вр:
Iш.вр =mш.вр.∙r∙ω2 (3.44)
где mш.вр = 2/3 mш.ш , кг - . масса вращающейся части шатуна.
Результирующая сила, действующая на шатунный подшипник,
Р'r =Pr - Iш.вр (3.45)
Результирующая сила, действующая на вал компрессора,
Р''r =Pr - (I i ш.ш.+ Iш.вр) (3.46)
Так как силы I ш.ш. и I ш.вр постоянны по величине и имеют отрицательный знак (направлены от оси вращения вала), для определения значений Р'r на диаграмме радиальных сил переносим ось абсцисс на величину I ш.вр. Для определения Р''r - на величину I ш.ш. + I ш.вр в сторону положительных значений ординаты.
Результаты расчета радиальных сил сводятся в таблицу
Таблица 6 Результаты расчета радиальных сил
α,º |
Р,Н |
|
Рr,Н |
α,º |
Р,Н |
|
Рr,Н |
0 |
|
|
|
180 |
|
|
|
15 |
|
|
|
195 |
|
|
|
… |
|
|
|
… |
|
|
|
180 |
|
|
|
360 |
|
|
|
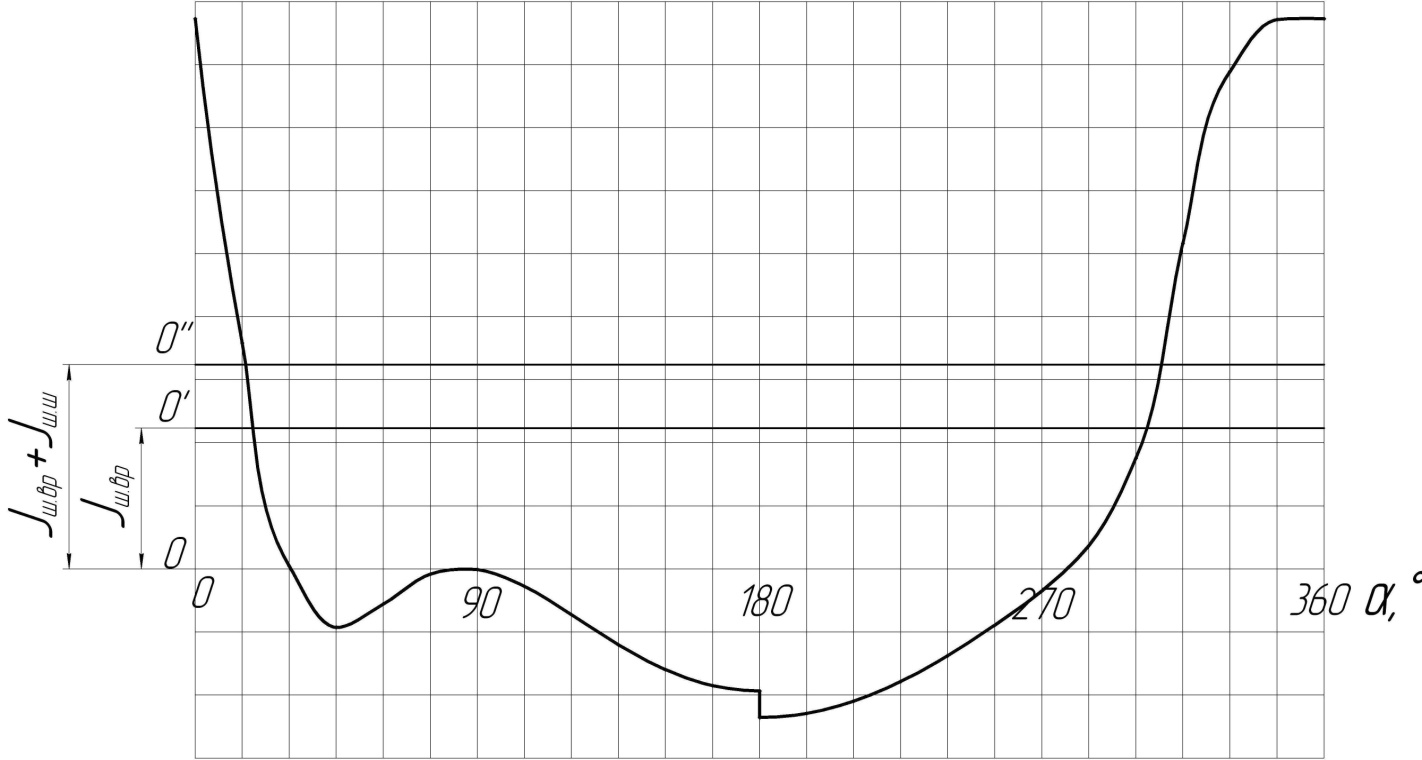
Рисунок 8 Диаграмма радиальных сил

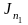 ,
Н
,
Н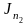 ,
Н
,
Н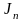 ,
Н
,
Н