Лабораторная работа 8
.docФедеральное агенство по образованию РФ
СПбГЭТУ «ЛЭТИ»
Кафедра МО-ЭВМ
Факультет КТИ
ОТЧЕТ
по лабораторной работе № 8
Метод Гаусса.
Дисциплина: вычислительная мпатематика
Студент группы 4351
Кузьменко А.
Преподаватель:
Щеголева Н.Л.
Санкт-Петербург
2006
Лабораторная работа № 8
Метод Гаусса.
1. Постановка задачи.
Используя
квадратурную формулу Гаусса наивысшего
порядка точности, вычислить приближенное
значение интеграла
.
2. Теоретические сведения.
В
квадратурной формуле Гаусса
узлы
и коэффициенты
подобраны так, чтобы формула была точна
для всех многочленов степени
.
Для приближенного вычисления интеграла
по конечному отрезку
выполняется замена переменной
;
тогда квадратурная формула Гаусса
принимает вид
,
где
;
- узлы квадратурной формулы Гаусса;
- гауссовы коэффициенты
.
Если подынтегральная функция достаточно гладкая, то формула Гаусса обеспечивает очень высокую точность при небольшом числе узлов.
Квадратурной формуле Гаусса с восемью узлами используется со следующими значениями узлов и коэффициентов:
,
;
,
;
,
;
,
.
3. Текст программ.
double Met_G (double a,double b)
{
double x [8] = {-0.96028986,-0.79666648,-0.52553242,-0.18343464, 0,0,0,0};
double A [8]= {0.10122854, 0.22238103, 0.31370664, 0.36268378, 0,0,0,0};
int i;
double s,t;
for (i=0;i<4;i++)
{
x[7-i]=-x[i];
A[7-i]=A[i];
};
for (i=0;i<8;i++)
s=0;
for (i=0;i<8;i++)
{
t=(a+b)/2+(b-a)/2*x[i];
s=s+A[i]*F(t);
}
s=s*(b-a)/2;
return (s);
}
#include "Met.h"
#include <iostream.h>
#include <conio.h>
void main()
{
clrscr;
cout<<"\n*** Программа вычисляет значение интеграла f= cos(x)/(1+x^2) на [0,1] ***\n"
<<"*** по квадратурной формуле Гаусса с 8 узлами ***\n"
<<"\Результат: "<<Met_G (0,1)<<endl;
getch();
}
double F(double x)
{
double s;
s=cos(x)/(1+x*x);
return s;
}
4. Вычислительный эксперимент.
График подынтегральной функции выглядит следующим образом:
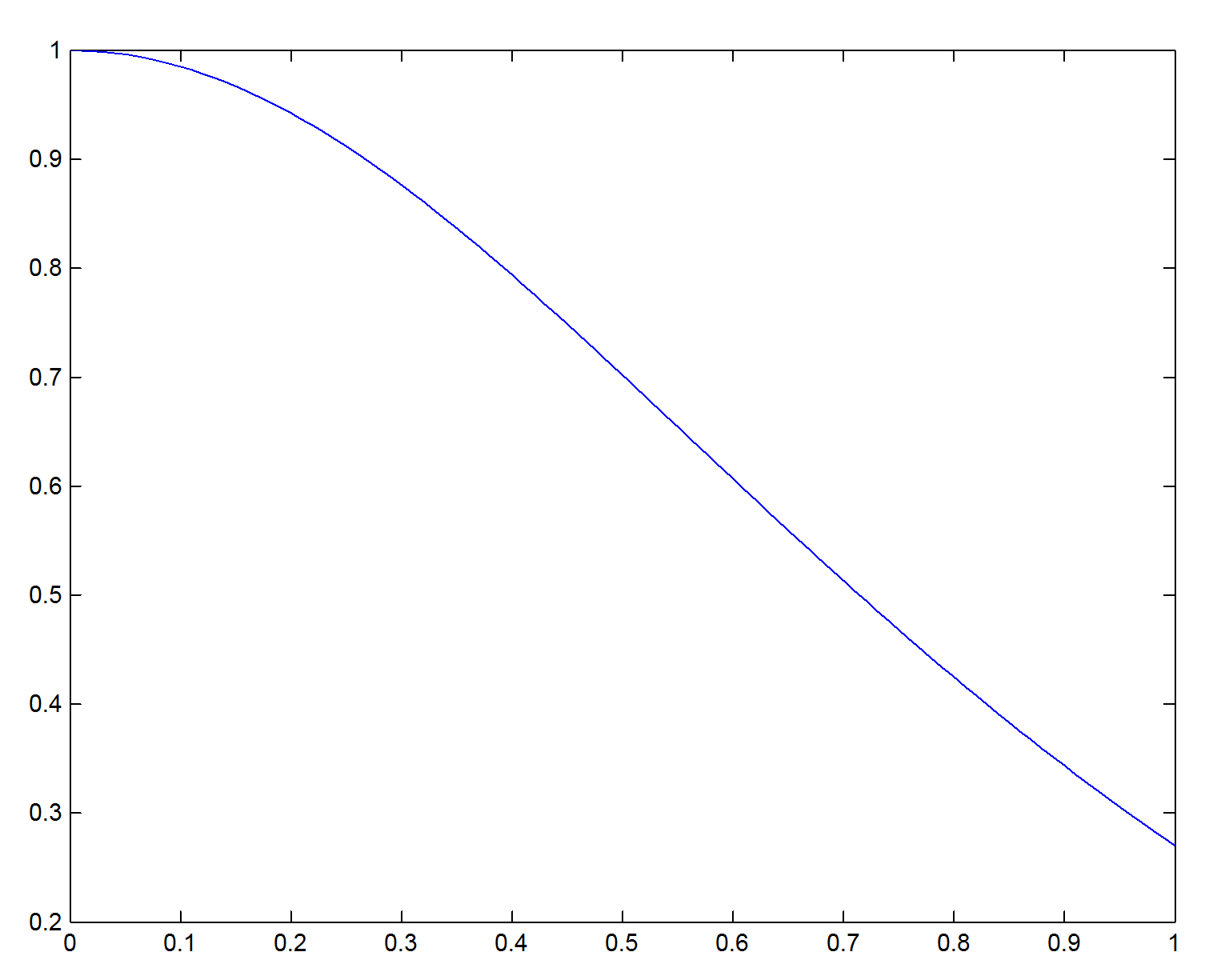
В результате
программа выводит значение 0,682933, что
соответствует истинному значению
с точностью до
10-6.
5. Выводы.
Квадратурная формула Гаусса имеет довольно высокую точность вычисления, так как в ней используются оптимальные значения узлов и весовых коэффициентов. Точность формулы Гаусса даже с двумя узлами превосходит точность результата по методу Симпсона.
Однако для применения метода Гаусса необходимо предварительно вычислить значения узлов и весовых коэффициентов.