2.2 Определение параметров автоколебаний в автоматической системе регулирования.

Предложим, что система автоматического регулирования, рассмотренная выше, имеет регулирующий орган с нелинейной характеристикой. Вид этой характеристики определяется по приложению.

Метод гармонической линеаризации основан на предложении, что колебания на входе нелинейного звена является синусоидальными, т.е. что

(22)

где А – амплитуда; _а – частота этих автоколебаний.

Колебания на выходе нелинейного звена будут так же гармоническими. Разложим выходные колебания у (t) в ряд Фурье и отбросим высшие гармонии (предполагая, что линейная часть системы пропускает только первую гармонику колебаний).

(23)

Здесь

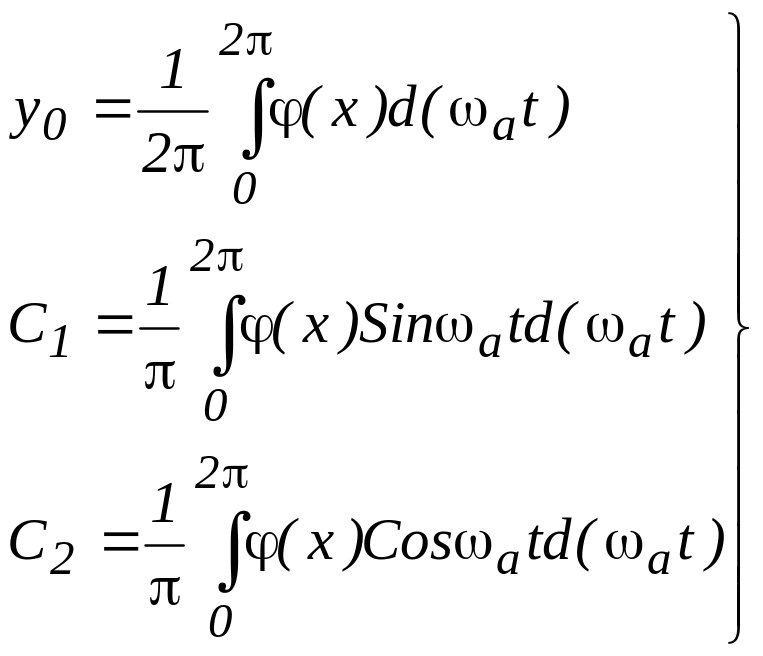(24)

Из уравнения (22) имеем

(25)

Продифференциировав это равенство, получим

(26)

Подставляя значения из (25) и (26) в (23), имеем

(27)

здесь введены обозначения

(28)

Дифференциальное уравнение (27) справедливо для синусоидального входного сигнала (22) и определяет выходной сигнал нелинейного звена без учета высших гармоник.

Постоянная составляющая у₀ и коэффициенты Кг и К^'г в соответствии с выражениями (24) являются функциями амплитуды А и частоты _а автоколебаний на выходе нелинейного звена. При фиксированных А и _а уравнение (27) является линейным.

Таким образом, если отбросить высшие гармоники, то для гармонического сигнала исходное нелинейное звено может быть заменено эквивалентным линейным, описываемым уравнением (27)

Коэффициенты Кг и К^'г определяются нелинейностью  (х) и значениями А и _а по формулам (24). Для типовых нелинейных звеньев имеются табличные значения этих коэффициентов.

Постоянная составляющая у₀ согласно (24), появляется в уравнении (27) только в случае нелинейностей, несимметричных относительно начала координат. В этом случае имеется эффект выпрямления чисто переменного сигнала. При симметричной относительности начала координат характеристике  (х) постоянная составляющая у₀ = 0 и уравнение (27) принимает вид

, (29)

или

(30)

где

- передаточная функция эквивалентного линейного звена, которую можно назвать гармонической передаточной функцией нелинейного звена.

В соответствии с (27) и (28) коэффициент Кг определяет выходную гармоническую составляющую, а коэффициент К^'г – выходную составляющую сдвинутую по фазе относительно входного сигнала на /2, вперед или назад, в зависимости от знака К^'г.

В общем случае автоколебания могут быть несимметричными, т.е. содержать постоянную составляющую. Тогда колебания на выходе нелинейного звена следует искать в виде

(31)

где х₀ – постоянная составляющая х.

В этом случае коэффициенты Фурье и, следовательно, значения у₀, Кг и К^'г в уравнении (27) оказываются уже функциями трех величин: _а, А и _а.

Наличие постоянной составляющей на входе нелинейного звена приводит к появлению постоянной составляющей на его выходе. Пи этом уравнение (27) удобно представить в виде

(32)

где Кг₀ = у₀/х₀ – коэффициент передачи постоянной составляющей автоколебаний.

Рассмотрим методику определения возможных автоколебаний в системе регулирования.

Рассмотрим вначале более простой случай, когда отыскиваются автоколебания в виде

(33)

т.е. без постоянной составляющей. Применив гармоническую линеаризацию, заменим нелинейное звено линейным, описываемым уравнением

(34)

В результате получим линейную САУ с передаточной функцией

(35)

где

Входящие в W_нл величины Кг (А, _а) и К^'г (А, _а) выражаем как линейные функции искомых неизвестных А и _а. В случае типовых нелинейностей используем готовые формулы.

Получаемая система является линейной только при фиксированных значениях А и _а. При их изменении система по прежнему нелинейна, т.к. содержит коэффициенты Кг и К^'г, являющиеся функциями этих величин.

Искомые параметры А и _а, входящих в передаточную функцию (35) линейной САУ, соответствуют наличию в этой системе незатухающих колебаний, т.е. нахождению ее на границе устойчивости. Это соответствует наличию у характеристического уравнения пары сопряженных чисто мнимых корней. Другими словами, значения А и _а могут быть найдены как значение переменных, при которых система автоматического регулирования находится на границе устойчивости. Для этого можно воспользоваться известными критериями устойчивости.

Условие наличия у характеристического уравнения мнимых корней по критерию Гурвица сводится к равенству

(36)

где - предпоследний минор определителя Гурвица

По критерию Найквиста то же условие имеет вид

(37)

или с учетом (35)

(38)

Из критерия Михайлова это условие можно получить в виде

(39)

где - характеристический полином замкнутой системы.

В результате находятся параметры возможных автоколебаний в системе, например, в виде зависимости А (_а).

Нелинейный характер зависимостей коэффициентов Кг и К^'г гармонической линеаризации от А и _а делает задачу нахождения искомых значений А и _а значительно более сложной, чем в случае определения границ устойчивости линейных систем. Поэтому обычно прибегают к методу последовательных приближений или к графическим методам.

Если характеристика нелинейного звена несимметрична относительно начала координат, автоколебания будут содержать постоянную составляющую (31). В этом случае в результате гармонической линеаризации нелинейное звено описывается линейным уравнением (32).

Постоянные составляющие х₀ и у₀ связаны передаточной функцией линейной части системы

(40)

В результате гармонической линеаризации у₀ определяется в виде функции А, _а и Х₀.

Для гармонической составляющей система по прежнему описывается передаточной функцией

где

Методика нахождения параметров автоколебаний остается принципиально прежней с той только разницей, что к А и _а прибавился третий параметр Х₀ и соответственно новое уравнение (40), которое следует решать совместно с прежними уравнениями, определяющими условия существования мнимых корней.

Если к системе автоматического регулирования приложенное постоянное воздействие F₀, оно создает постоянный сигнал на входе нелинейного звена, и автоколебания в системе будут несимметричными даже в случае симметричной нелинейной характеристики. Уравнение для постоянной составляющей в этом случае имеет вид

(41)

где W_FX – передаточная функция между точкой приложения F₀ и Х, а F₀ - известное постоянное воздействие.