
- •Раздел второй кинетика
- •4. Кинетика
- •4.1. Введение в кинетику
- •4.1.1. Предмет кинетики. Основные понятия
- •4.1.2. Основные законы механики
- •4.1.3. Связи и реакции связей
- •4.1.4. Силы трения
- •4.1.5. Классификация связей
- •Вопросы для повторения
- •4.2. Дифференциальные уравнения движения материальной точки
- •4.2.1. Дифференциальные уравнения движения свободной точки
- •4.2.2. Движение несвободной материальной точки
- •4.2.3. Дифференциальные уравнения относительного движения материальной точки
- •4.2.4. Две основные задачи динамики
- •Вопросы для повторения
- •4.3. Введение в динамику механической системы
- •4.3.1. Дифференциальные уравнения движения механической системы
- •4.3.2. Силы, действующие на абсолютно твердое тело
- •4.3.3. Распределенные силы. Центр тяжести
- •4.3.4. Момент силы относительно точки и относительно оси
- •4.3.5. Пара сил
- •4.3.6. Главный вектор и главный момент системы сил. Свойства внутренних сил
- •4.3.7. Приведение системы сил к данному центру
- •4.3.8. Масса и центр масс системы материальных точек
- •4.3.9. Моменты инерции
- •4.3.10. Моменты инерции простейших однородных тел
- •Вопросы для повторения
- •4.4. Теоремы об изменении количества движения и о движении центра масс
- •4.4.1. Количество движения материальной точки и системы материальных точек. Элементарный и полный импульсы силы.
- •4.4.2. Теорема об изменении количества движения системы
- •4.4.3. Теорема о движении центра масс
- •4.4.4. Дифференциальные уравнения поступательного движения твердого тела
- •Вопросы для повторения
- •4.5. Теорема об изменении кинетического момента
- •4.5.1. Кинетический момент точки
- •4.5.2. Кинетический момент системы материальных точек
- •4.5.3. Теорема об изменении кинетического момента системы материальных точек
- •4.5.4. Дифференциальное уравнение вращательного движения твердого тела
- •Вопросы для повторения
- •4.6. Теорема об изменении кинетической энергии
- •4.6.1. Кинетическая энергия точки и системы точек
- •4.6.2. Работа силы
- •4.6.3. Работа силы, приложенной к вращающемуся твердому телу
- •4.6.4. Работа внутренних сил
- •4.6.5. Мощность
- •Вопросы для повторения
- •4.6.6. Теорема об изменении кинетической энергии
- •Вопросы для повторения
- •4.6.7.* Потенциальное силовое поле
- •4.6.8.* Потенциальная энергия
- •4.6.9*. Закон сохранения механической энергии
- •Вопросы для повторения
- •5. Статика
- •5.1. Условия равновесия системы сил, приложенных к твердому телу
- •5.2. Теорема Вариньона о моменте равнодействующей
- •5.3. Условия равновесия систем сходящихся и параллельных сил
- •5.4. Условия равновесия плоской системы сил
- •Решив эту систему, получим
- •5.5. Равновесие системы тел. Примеры решения задач
- •Вопросы для повторения
- •5.6.* Принцип возможных перемещений
- •Вопросы для повторения
- •6. Принцип даламбера
- •6.1. Принцип Даламбера для материальной точки
- •6. 2. Принцип Даламбера для системы материальных точек
- •6. 3 *. Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси
- •6.4*. Общее уравнение динамики
- •Вопросы для повторения
- •Список литературы Основная
- •Дополнительная
- •4.1. Введение в кинетику ………………………………… . ..141
- •4.1.1.Предмет кинетики. Основные понятия………… ……..141
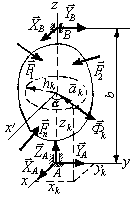
6. 3 *. Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси
Пусть
на твердое тело, вращающееся вокруг оси
АВ (рис. 6.5) с постоянной угловой
скоростью ω, действует система сил (![]() )
главный вектор которой равен
,
а главный момент относительно точки А
равен
)
главный вектор которой равен
,
а главный момент относительно точки А
равен
![]()
 .
.
Так как вращение
равномерное, то проекция главного
момента на ось вращения равна нулю
![]() =
0 и, следователь-но,
=
0 и, следователь-но,
![]() лежит в плоскости Аху. Определим
реакции подшипника В и подпятника
А.
лежит в плоскости Аху. Определим
реакции подшипника В и подпятника
А.
Рис. 6.5 Для этого мысленно отбросим связи, заменив их реакциями
(![]() ).
).
Приложим к каждой
точке тела силу инерции
![]() ,
ввиду равномерности вращения (ε
= 0) равную Фk=mkω2hk,
и составим уравнения равновесия
полученной системы сил:
,
ввиду равномерности вращения (ε
= 0) равную Фk=mkω2hk,
и составим уравнения равновесия
полученной системы сил:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Так как Фkх = mkω2hk,cosα = mkω2хk и
Фkу = mkω2hk,sinα = mkω2уk,
то
![]()
![]()
![]()
![]()
где хС, уС — координаты центра масс тела, Jyz, Jzx — центробежные моменты инерции тела. Динамические реакции находятся из уравнений
ХА+ХВ= - Rx - Mω2 xC, YA + Y В= - Ry - Mω2 yC,
ZA= - Rz, YBb = Mz - ω2 Jyz, ХBb = - My - Jxz (6.11)
и будут отличаться от статических реакций, которые получаются из этих же уравнений при ω= 0.
Для того, чтобы вращение не вызывало дополнительных нагрузок на подшипники, должны выполняться условия
xC= 0, уC = 0, Jyz=0, Jxz = 0 , (6.12)
означающие, что:
1) центр масс тела должен лежать на оси вращения;
2) ось вращения должна быть главной осью инерции в точке А, то есть с учетом первого условия ось вращения должна быть главной центральной осью инерции тела.
Этот же вывод справедлив и для неравномерного вращения. Проблема ликвидации дополнительных динамических реакций в подшипниках вращающихся частей и деталей машин до сегодняшнего дня остается одной из важнейших в машиностроении.
6.4*. Общее уравнение динамики
Как было показано, принцип Даламбера позволяет записывать динамические уравнения движения в виде уравнений равновесия, так как при добавлении сил инерции к активным силам и силам реакций связей, действующим на систему, получается уравновешенная система сил. Но если система сил уравновешена, то к ней применим принцип возможных перемещений. Применение этих принципов к движущейся механической системе, на которую наложены идеальные стационарные голономные удерживающие связи, позволяет сформулировать принцип Даламбера—Лагранжа: Если к движущейся механической системе, на которую наложены идеальные стационарные голономные удерживающие связи, условно приложить силы инерции всех ее точек, то в каждый момент времени сумма элементарных работ активных сил и сил инерции равна нулю на любом возможном перемещении системы, то есть
![]() ,
или
,
или
![]() ,
(6.13)
,
(6.13)
или
![]() Действительно,
умножив каждое из равенств (6.3), выражающих
принцип Даламбера для системы материальных
точек, на
,
получим
Действительно,
умножив каждое из равенств (6.3), выражающих
принцип Даламбера для системы материальных
точек, на
,
получим
![]() ,
( k=1,2,...,
n).
,
( k=1,2,...,
n).
Просуммируем эти равенства по всем точкам системы:
![]() .
(6.14)
.
(6.14)
Но при идеальных
связях
![]() ,
и поэтому окончательно получаем
,
и поэтому окончательно получаем
![]() ,
(6.15)
,
(6.15)
что и требовалось доказать.
Равенство (6.15), выражающее принцип Даламбера — Лагранжа, называется общим уравнением динамики.
Общее уравнение динамики применяется при составлении дифференциальных уравнений движения системы материальных точек с одной или несколькими степенями свободы.
П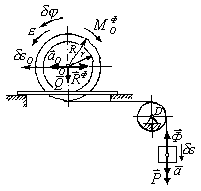 ример.
Груз А
массой т1,
который подвешен на невесомой
нерастяжимой нити, переброшенной через
невесомый блок D
и намотанной на шкив В
радиусом R,
заставляет связанный со шкивом вал
радиусом r
катиться
без скольжения по горизонтальному
рельсу (рис. 142). Общая масса шкива и
вала равна т2,
их радиус инерции относительно
центральной оси равен ρ.
Найти ускорение груза А.
ример.
Груз А
массой т1,
который подвешен на невесомой
нерастяжимой нити, переброшенной через
невесомый блок D
и намотанной на шкив В
радиусом R,
заставляет связанный со шкивом вал
радиусом r
катиться
без скольжения по горизонтальному
рельсу (рис. 142). Общая масса шкива и
вала равна т2,
их радиус инерции относительно
центральной оси равен ρ.
Найти ускорение груза А.
Решение.
Связи, наложенные на систему, являются
идеальными, поэтому приложим к системе
только активные силы (![]() ,
,
![]() ),
и силы инерции (
),
и силы инерции (![]() ).
).
Рис. 6.6 При этом
Ф
= m1а,
RФ=
m2аО,
![]()
Так как из кинематики механизма следует, что
ω = vА/(R - r), vО = ωr = vАr/(R-r),
то aO=ar/(R -r) и выражения для сил инерции и их момента примут вид
![]() ,
,
![]()
Дадим
системе возможное перемещение (![]() )
и подсчитаем на нем сумму возможных
работ:
)
и подсчитаем на нем сумму возможных
работ:
![]()
Из кинематики следует, что и поэтому
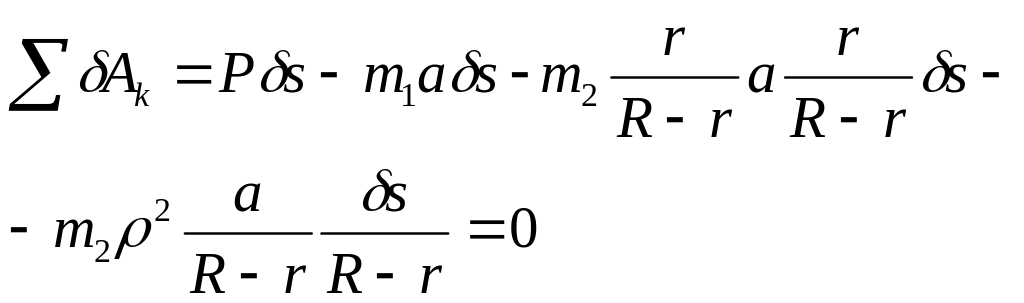
Сократив на δs, окончательно получим
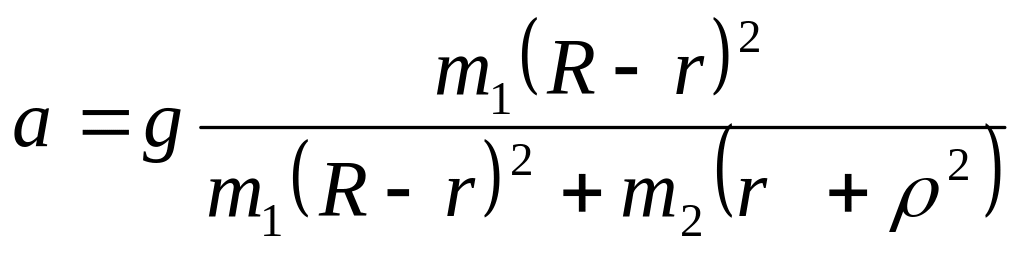 .
.
