5.4. Условия равновесия плоской системы сил

В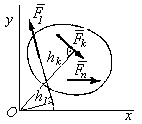 заключение рассмотрим еще один частный случай, а именно систему, все силы которой расположены в од­ной плоскости (такая система сил называется плоской), и найдем аналитические условия ее равновесия. Для это­го совместим плоскость осей Оху с плоскостью действия сил системы (рис. 5.7); тогда проекции всех сил на ось Oz и моменты всех сил относительно осей Ох и Оу рав­ны нулю и

Рис. 5.7 уравнения

, , ,

выполняются тождественно. Поэтому из шести уравнений (5.2) равновесия произвольной систе­мы сил остаются только три:

, , .

Последнее условие можно несколько упростить. Посколь­ку все силы лежат в плоскости Оху, то их моменты относительно оси Oz равны их алгебраическим моментам относительно точки О:

.

Тог­да и, следо­вательно, условия равновесия пло­ской системы сил принимают вид

, , . (5.8)

то есть для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы сумма проекций сил на каждую из двух взаимно перпендику­лярных осей координат, лежащих в плоскости действия сил, и сумма алгебраических моментов этих сил относи­тельно любой точки данной плоскости были равны нулю.

Кроме этой основной формы условий равновесия плос­кой системы сил часто используются еще две формы, которые являются следствием уравнений (5.8) и приво­дятся без доказательства.

Вторая форма условий равновесия: для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических мо­ментов сил системы относительно трех произвольных то­чек, расположенных в плоскости действия сил и не лежащих на одной прямой, равнялись нулю, т. е.

, , . (5.9)

Третья форма условий равновесия: для равновесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы алгебраических мо­ментов сил относительно двух точек А и В, лежащих в плоскости действия сил, и сумма проекций этих сил на ось, лежащую в этой плоскости и не перпендикулярную прямой, проходящей через точки А и В, равнялись нулю, то есть

, , , (5.10)

причем ось Ox не перпендикулярна прямой АВ.

П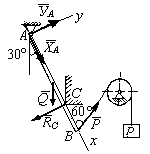 ример 1. Однородный стержень АВ длиной l= 40 см и весом Q=200 Н шарнирно закреплен в точке А и свободно опи­рается на опору С (рис. 5.8). К концу B стержня привязана ве­ревка, перекинутая через блок D и несущая на своем конце груз весом Р = 100 Н. Расстояние АС = 30 см. Пренебрегая трением в блоке, найти реакции опор.

Решение. Рассмотрим равновесие стержня АВ. На него дей­ствуют вес Q, сила натяжения троса, равная весу груза, а также реакции опор А и С.

Рис. 5.8 Реакция опоры С перпендикулярна стерж­ню; поэтому проведем оси Ах и Ау вдоль стержня и перпендику­лярно ему (это упростит уравнения равновесия) и разложим ре­акцию цилиндрического шарнира А на составляющие Х_А и У_А. Составим уравнения равновесия плоской системы сил, действую­щей на стержень:

(1) ; Х_А + Q cos 30^˚ - Р cos 60° = 0,

(2) ; У_А – Q cos 60° +р sin 60° - R_С = 0,

(3) ; - Q cos 60° ·AE - R_С·AC +P cos 30^˚ ·AB = 0.