4.3.7. Приведение системы сил к данному центру

Как известно, силу, приложенную к абсолютно твердому телу, можно переносить вдоль линии действия в любую точку тела. Докажем теперь, что

силу, приложенную к абсолютно твердому телу, можно переносить параллельно самой себе в любую точку тела, добавляя при этом пару сил с моментом, равным моменту переносимой силы относительно ее новой точки приложения.

Пусть сила приложена в точке А тела (рис. 4.36, а) Приложим в точке В, куда мы хотели бы перенести силу , уравновешенную систему сил таких, что

Р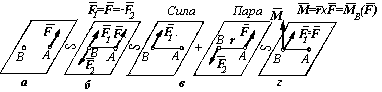 ис. 4.36

(рис. 4.36, 6). Тогда ~ .

Силы и образуют пару сил, поэтому полученную систему трех сил можно рассматривать как совокупность силы , приложенной в точке В, и пары сил (рис. 4.36, в). Пара сил определяется ее моментом , равным. моменту силы относительно точки В: . Таким обра­зом, исходная сила , приложенная в точке А, эквивалентна гео­метрически равной ей силе, приложенной в точке В, и паре сил с моментом равным моменту силы относительно центра В (рис. 4.36, г), что и требовалось доказать.

Теперь рассмотрим произвольную систему сил , приложенную к абсолютно твердому телу (рис. 4.37, а). Докажем, что эта система сил эквивалентна совокупности одной силы и паре сил.

Процесс замены системы сил одной силой и парой сил называется приведением к заданному центру.

Выберем в теле произвольную точку О, которую назовем цент­ром приведения Пользуясь только что доказанной теоремой о па­раллельном переносе силы, перенесем в точку О параллельно са­мим себе все силы системы, добавляя каждый раз пару сил с моментами,

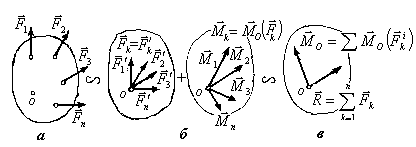
Рис. 4.37

равными моментам переносимой силы относительно центра приведения О. В результате этой операции мы получим систему сходящихся сил таких, что , и систему пар сил ( ), моменты которых равны мо­ментам исходных сил относительно точки О: (рис. 4.37, б). Как было доказано выше, систему сходящихся сил можно заменить ее равнодействующей

,

а систему пар сил — одной парой с моментом, равным векторной сумме моментов слагаемых пар:

.

Таким образом, исходная система сил заменена одной силой и одной парой сил с моментом (рис. 4.37, в), что и требовалось доказать. По определению, данному в предыдущем параграфе, полученная сила и момент пары сил являются главным вектором и главным моментом исходной системы сил в точке О.

Следовательно, произвольная система сил, приложенных к аб­солютно твердому телу, в результате приведения ее к произволь­ному центру может быть заменена одной силой, равной главному вектору исходной системы сил, и одной парой сил, с моментом, равным главному моменту исходной системы сил относительно точки О, причем

, . (4.54)

4.3.8. Масса и центр масс системы материальных точек

Масса М системы п материальных точек равна арифметической сумме масс т_k всех ее точек, то есть

(4.55)

Центром масс системы п материальных точек назы­вается геометрическая точка С, радиус-вектор которой определяется выражением

(4.56)

где — радиус-вектор k-й точки. Спроектировав это равенство на оси координат, получим выражения для координат центра масс системы материальных точек:

, , , (4.57)

где — координаты точек системы. Если центр масс находится в начале координат, то = 0 и, следовательно,

,

или

, , . (4.58)

Для тел малых размеров, находящихся вблизи по­верхности Земли, можно принять, что m_k = P_k/g, где Р_k — вес k-й точки, и поэтому выражение для радиус-вектора центра масс принимает вид

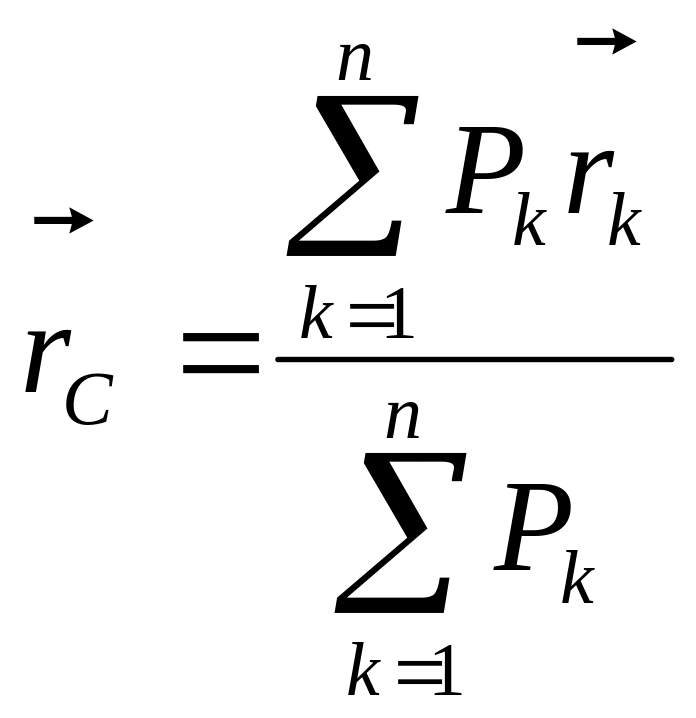(4.59)

То есть при инженерных расчетах можно считать, что центр масс совпадает с центром тяжести механической системы.