4.3.2. Силы, действующие на абсолютно твердое тело

Как уже говорилось, мерой механического взаимодействия материальных тел является сила, то есть векторная величина, определяемая модулем, направлением и точкой приложения. Поскольку теоретическая механика изучает движение абсолютно твердого тела, то приложенные к этому телу силы обладают рядом особенностей.

Очевидно, что две силы, приложенные к абсолютно твердому телу, не изменят его состояния движения или покоя, если они равны по величине и направлены в противоположные стороны по одной прямой. Так как эти силы образуют уравновешенную систему, то есть эквивалентную нулю ~0. Ясно так же, что если к свободному твердому телу приложить уравновешенную систему сил или отбросить такую систему, то его состояние движения или покоя не изменится.

И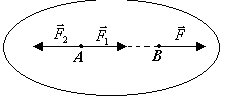 з этих двух очевидных положений следует, что силу, приложенную к абсолютно твердому телу, не изменяя его состояния покоя или движения, можно перенести вдоль линии действия в любую точку тела. Действительно, пусть сила приложена в точке А тела (рис. 4.17). Приложим в точке В,

Рис. 4.17 лежащей на линии действия силы уравновешенную систему сил , таких что . Тогда ~ Но система сил , равных по модулю, противоположных по направлению и имеющих общую линию действия, эквивалентна нулю и может быть отброшена. Тогда ~ , что и требовалось доказать.

Если к одной точке твердого тела приложены несколько сил, то, как и в случае действия такой системы сил на материальную точку, они могут быть заменены одной силой – равнодействующей, равной геометричес-кой сумме этих сил и приложенной в этой же точке.

Рассмотрим теперь систему действующих на абсолютно твердое тело сил, линии действия которых пересекаются в одной точке (рис. 4.18). Такие силы называются сходящимися. На основании доказанного свойства о переносе силы вдоль линии ее действия данная система сил эквивалентна системе сил, приложенных к одной точке (точка А на рис. 4.18), а такая система сил имеет равнодействующую. Таким образом, система сходящихся сил имеет равнодействующую, равную геометрической сумме сил системы и приложенную в точке пересечения их линий действия.

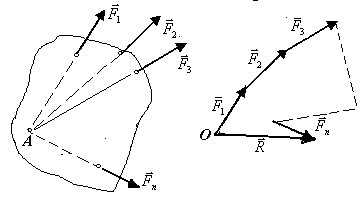
Рис. 4.18

Если же на абсолютно твердое тело действуют две одинаково направленные параллельные силы и (рис. 4.19), приложенные в точках А и В соответственно, то их равнодействующая имеет направление слагаемых сил и модуль, равный сумме модулей исходных сил, а точка ее приложения делит отрезок, соединяющий точки

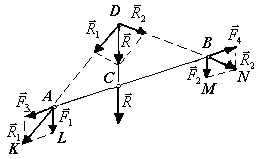
Рис. 4.19

приложения сил, на части, обратно пропорциональные слагаемым силам, т.е.

; . (4.34)

Чтобы доказать это, приложим в точках А и В уравновешенную систему сил , линии действия которых совпадают с прямой АВ; = - . Полученная система сил будет эквивалентна исходной .

Системы сил и можно заменить соответствующими равнодействующими и , а полученные в результате сходящиеся силы и тоже заменить их равнодействующей , приложенной в точке D. Так как =- и ║ , то , а ее модуль равен сумме модулей слагаемых сил: . Перенесем вдоль линии ее действия в точку С, лежащую на прямой АВ. В результате исходная система сил заменится одной силой — равнодействующей , направленной в сторону слагаемых сил и приложенной в точке С отрезка АВ. Из построений на рис. 4.19 следует, что треугольник ADC подобен тре­угольнику KAL, а треугольник CDB — треугольнику MBN, поэтому AC/KL = DC/AL и BC/MN = DC/BM. Учиты­вая, что KL = MN = , AL = , ВМ = , окончательно получим

,

что и требовалось доказать.

А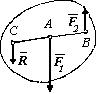 налогично доказывается и случай, когда параллель­ные силы и имеют противоположные направления (рис. 4.20). Тогда их равнодействую-щая по модулю равна разности

Рис. 4.20 модулей слагаемых сил и имеет направление большей силы, а точка ее приложения С делит отрезок АВ на ча­сти, обратно пропорцио­нальные силам, но внеш­ним образом, то есть

, .

Ясно, что по этим же правилам мы можем раз­ложить одну силу на две параллельные ей составляющие, приложенные в заданных точках тела.

Рассмотрим случай, когда система одинаково направленных параллельных сил , приложенных в точках M₁, М₂, ..., М_n тела (рис. 4.21). По правилу сложения параллельных сил (4.34) мы можем заменить силы и силой + , приложенной в точке C₁. Складывая получен­ную силу с силой ,

з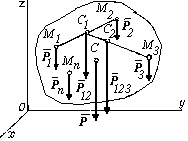 аменим их равнодействующей ,

приложенной в точке С₂. Последовательно складывая вновь полученную равнодей­ствующую с последующей силой системы, придем к од­ной силе ,

Рис. 4.21 являющейся равнодействующей исходной системы сил и приложенной в опре­деленной точке С тела. Найдем координаты этой точки, считая координаты точек приложения сил системы из­вестными. Точка С, делит отрезок М₁М₂ на части, об­ратно пропорциональные силам и , то есть

.

Но, как известно из аналитической геометрии, координаты точки C₁, делящей отрезок в таком отноше­нии, определяются выражениями

, , .

Аналогичным образом координаты точки C₂ приложения силы определяются ( ) так:

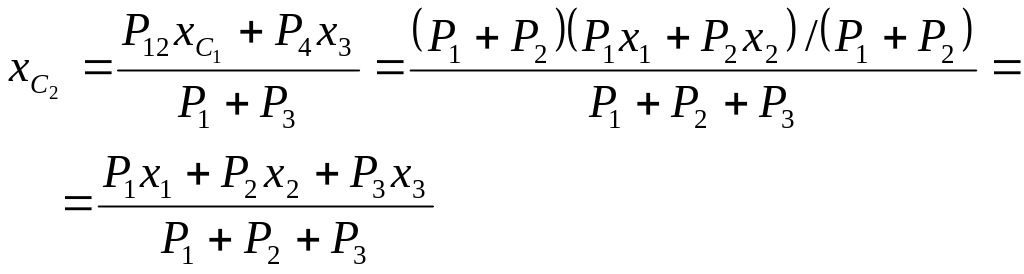и т. д.

Таким образом, по индукции можно заключить, что си­стема одинаково направленных параллельных сил действующих на абсолютно твердое тело, име­ет равнодействующую, параллельную силам системы, равную сумме всех сил системы

(4.35)

и приложенную в точке С, координаты которой определяются выражениями

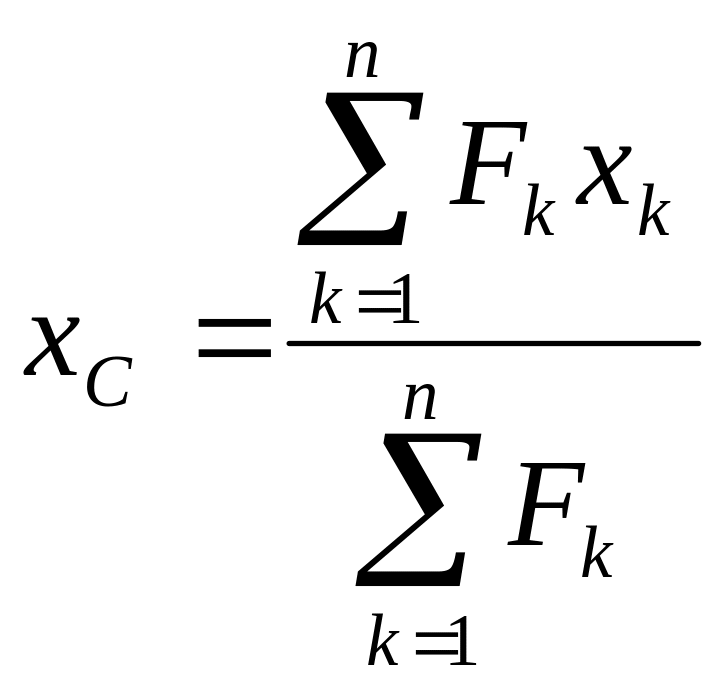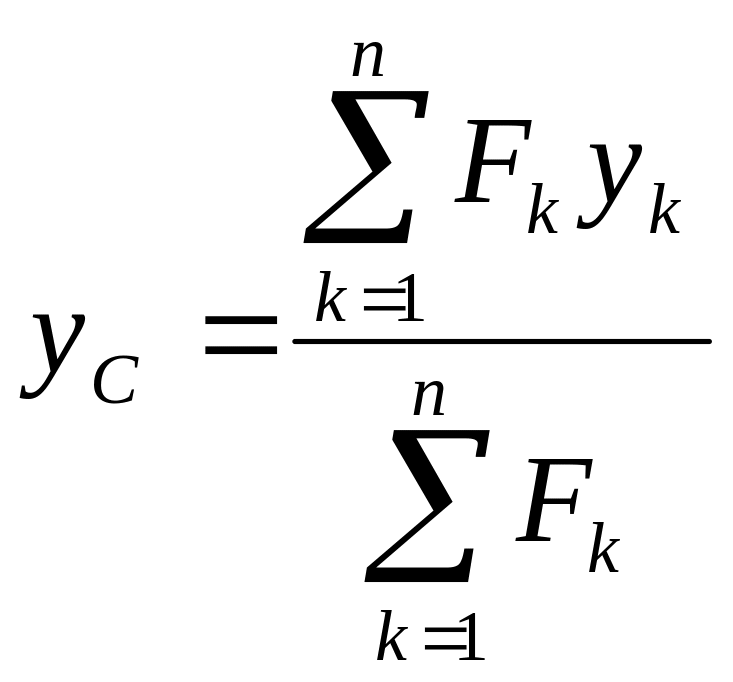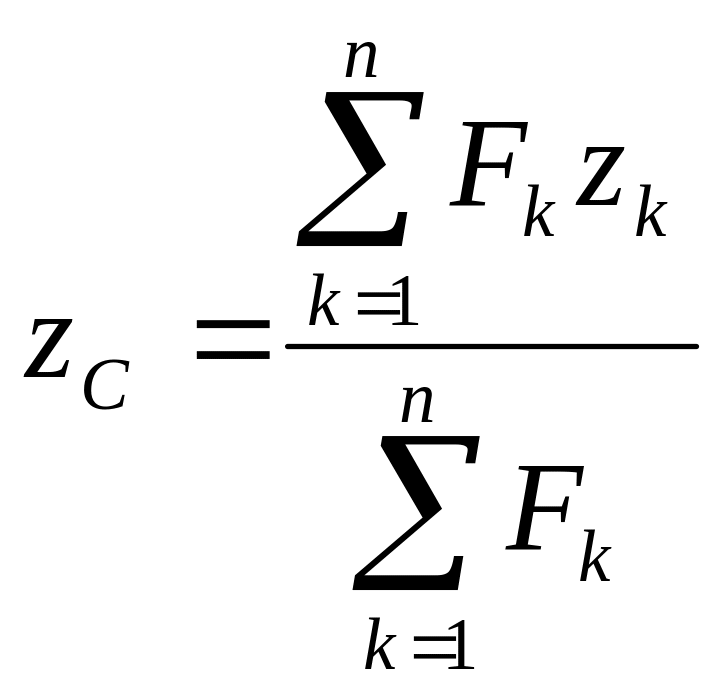, , , (4.36)

где x_k,, y_k, z_k — координаты точек приложения сил системы.