II. Динамика.

§ 1. Определение координат центра масс тела.

В однородном поле тяжести, для которого g = const, вес любой частицы тела будет пропорционален ее массе. Поэтому о распределении масс в теле можно судить по положению его центра тяжести. Преобразуем формулы, определяющие координаты центра тяжести к виду, явно содержащему массу

; ;

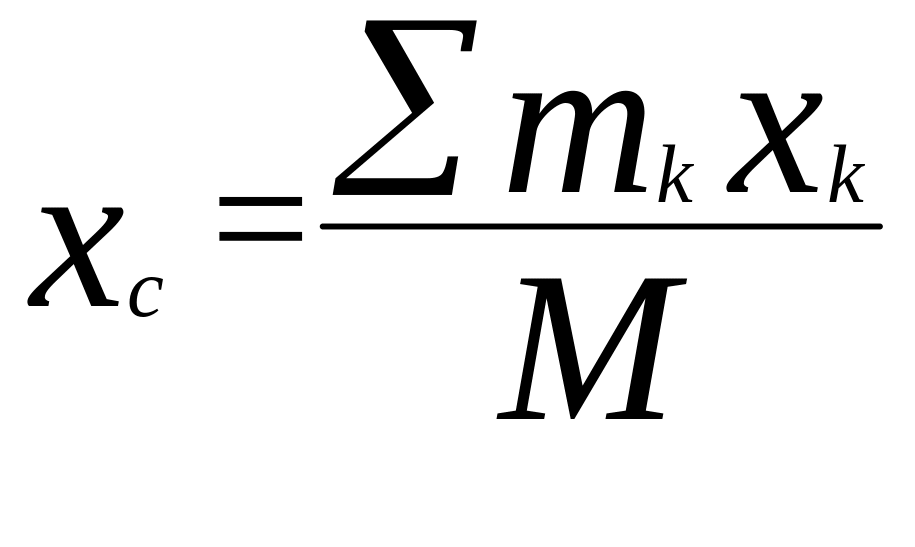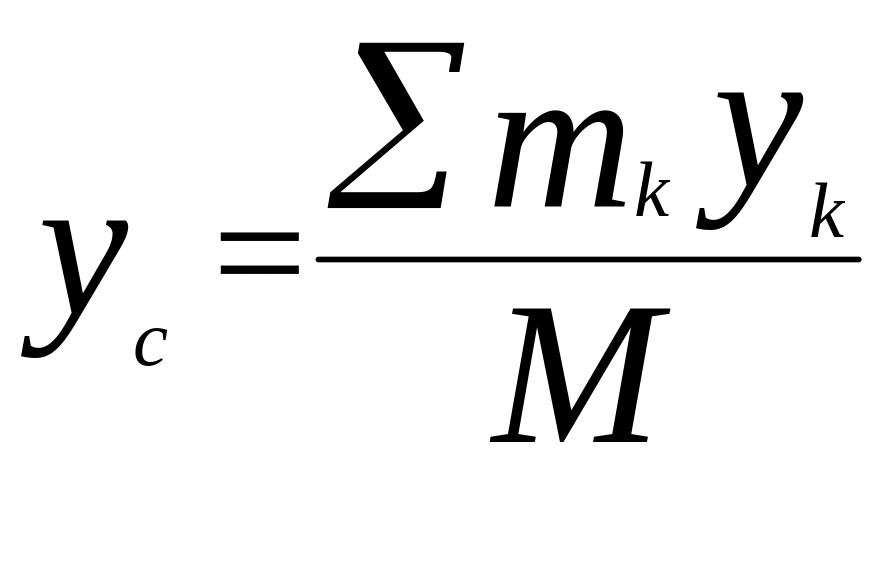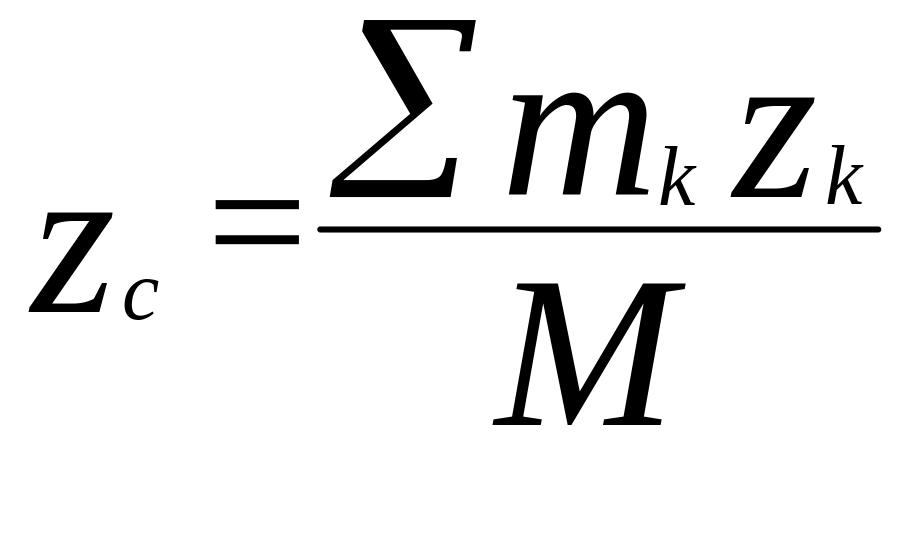
, -радиус-вектор точек, образующих систему.

Геометрическая точка C, координаты которой определяются этими формулами, называется центром масс или центром инерции механической системы.

Хотя положение центра масс совпадает с положением центра тяжести тела, находящегося в однородном поле тяжести, понятия эти не являются тождественными. Понятие о центре тяжести как о точке, через которую проходит линия действия равнодействующей сил тяжести, имеет смысл только для твердого тела, находящегося в однородном поле тяжести. Понятие же о центре масс, как о характеристике распределения масс в системе, имеет смысл для любой системы материальных точек или тел, причем это понятие сохраняет свой смысл независимо от того, находится ли данная система под действием каких-либо сил или нет.

§ 2. Дифференциальные уравнения движения системы.

Рассмотрим систему, состоящую из n материальных точек. Выделим какую-нибудь точку с массой m_k. Обозначим равнодействующую всех приложенных к точке внешних сил (и активных, и реакций связей) через , а равнодействующую всех внутренних сил - .

;

Для n материальных точек

;

;

…………………….;

.

Эти уравнения называются дифференциальными уравнениями движения системы. Уравнения являются дифференциальными, так как W_k= , силы тоже в общем случае зависят от времени, координат точек и скоростей.

В ряде случаев для определения характера движения системы достаточно знать закон движения ее центра масс.

Сложим почленно левые и правые части:

;

Ранее было получено:

.

Возьмем из обеих частей вторую производную по времени:

; .

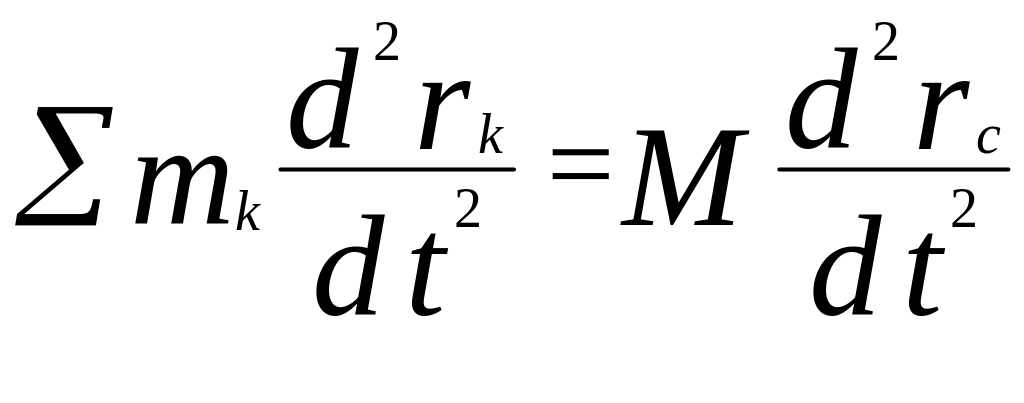Сумма всех внутренних сил равна 0:

Окончательно получим:

Это есть теорема о движении центра масс:

Произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил.

§ 3. Принцип Даламбера.

Векторную величину, равную по модулю произведению массы точки на ее ускорение и направленную противоположно этому ускорению, называют силой инерции точки.

Принцип Даламбера: Если в любой момент времени к каждой из точек системы, кроме внешних и внутренних сил, приложить соответствующие силы инерции, то полученная система сил будет находиться в равновесии, и к ней можно будет применять все уравнения статики.

Математически принцип Даламбера выражается системой n векторных равенств вида:

§ 4. Принцип возможных перемещений.

Возможным перемещением системы мы будем называть любую совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент всеми наложенными на систему связями.

В общем случае для точек и тел системы может существовать множество различных возможных перемещений. Однако, для каждой системы можно указать определенное число таких независимых между собой перемещений, что всякое другое возможное перемещение будет получаться как их геометрическая сумма.

Число независимых между собой возможных перемещений системы называется числом степеней свободы этой системы. Шарик на плоскости имеет 2 степени свободы. У свободной материальной точки 3 степени свободы (3 перемещения вдоль взаимно перпендикулярных осей). Свободное твердое тело имеет 6 степеней свободы (3 поступательных перемещения вдоль осей координат и 3 вращательных вокруг этих осей).

Для равновесия механической системы необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.

Выделим произвольную точку B_k системы и обозначим равнодействующую всех приложенных к ней активных сил (внешних и внутренних) через F^а_k, δx_k, δy_k, δz_k – проекции возможного перемещения δS_k точки B_k на оси координат. Они равны элементарным приращениям координат этой точки при её перемещении и вычисляются так же, как дифференциалы координат.

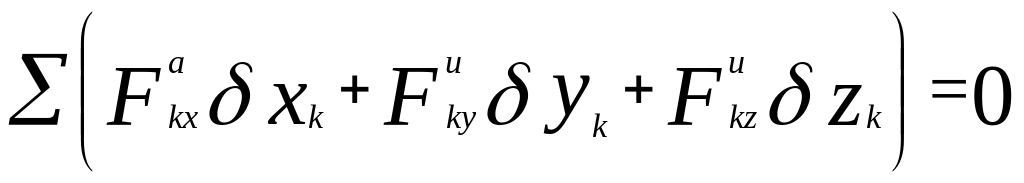
Задача.

В механизме, изображенном на чертеже, найти зависимость между силами P и Q при равновесии.

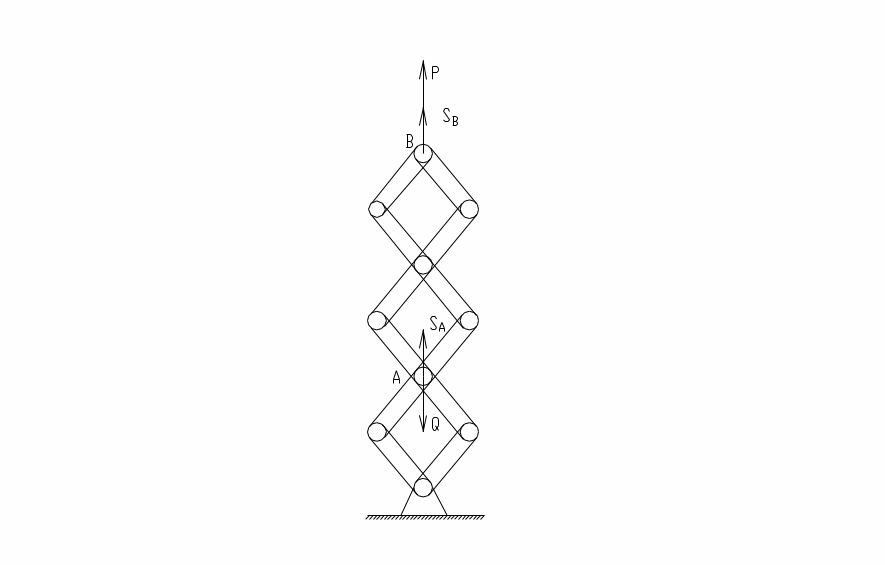
Если сообщить системе возможное перемещение, то все диагонали параллелограммов, образованных стержнями, удлинятся на одну и ту же величину δs. Тогда δS_A=δs, δS_B=3δs.

PδS_B-QδS_A=0 или (3P-Q)δs=0 Q=3P