Реляционная алгебра

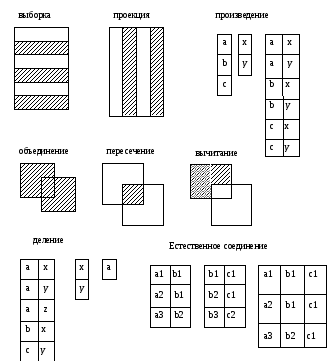
Реляционная алгебра состоит из операторов, объединенных в две группы:

1. Классические операции над множествами: объединение, вычитание, пересечение, декартово произведение.

2. Специальные реляционные операции: выборка (селекция, ограничения), проекция, деление, операция переименования.

Определения:

1. Выборка– возвращает отношение, содержащее все кортежи, удовлетворяющие одному условию.

2. Проекция- возвращает отношение, содержащее все кортежи исходного отношения после исключения из него некоторых атрибутов.

3. Произведение- возвращает отношение, содержащее всевозможные кортежи, являющиеся сочетанием двух кортежей, принадлежащих соответственно двум исходным отношениям.

4. Объединение – возвращает отношение, содержащее все кортежи, принадлежащие одному из двух исходных отношений или двум сразу.

5. Пересечение- возвращает отношение, содержащее все кортежи, принадлежащие одновременно двум исходным отношениям.

6. Вычитание- возвращает отношение, содержащее все кортежи, принадлежащие одному из двух исходных отношений или двум сразу.

7. Соединение - возвращает отношение, кортежи которого – это сочетание двух кортежей, принадлежащих, соответственно, двум исходным отношениям, имеющих общее значение для одного или нескольких атрибутов этих двух исходных отношений. Такие общие значения в результате появляются один раз.

8. Деление – для двух отношений бинарного и унарного возвращает отношение, содержащее все значения одного атрибута бинарного отношения, которые соответствуют в другом атрибуте всем значениям в унарном отношении.

Результат каждой операции над отношением также является отношением. Это называется свойством замкнутости. Т.о. реляционная алгебра допускает вложенные выражения, в которых операнды вместо имен отношений сами могут быть выражениями.

Реляционная алгебра должна включать в себя также набор правил наследования имен атрибутов, чтобы можно было предсказывать имена атрибутов на выходе любой реляционной операции, зная имена атрибутов на входе. Реляционная алгебра должна быть определена т.о., чтобы все отношения имели правильные заголовки (схемы), т.е. заголовки, в которых все атрибуты имеют правильные имена, правильные и уникальные в данном отношении. Для этого используются операция RENAME, предназначенная для переименования атрибутов в некотором отношении. Для некоторого отношения оператор RENAME возвращает новую копию отношения, в которой некоторый атрибут имеет другое заданное имя. Реляционная алгебра так же должна иметь набор правил наследования потенциальных ключей.

Нотация для реляционной алгебры (BNF)

Выражение

: := унарное выражение | бинарное выражение

унарное выражение

: := переименование | выборка | проекция

переименование

: := term rename | attribute As attribute

term

: := отношение | (выражение)

выборка

::= term where condition

проекция

::= term | term (список атрибутов)

бинарное выражение

::= проекция бинарная операция выражение

бинарная операция

::= union | intersect | minus | times | join | dirideby

Классические операции над отношениями: (объединение, вычитание, пересечение и произведение.)

Два отношения совместимы по типу, если имеют идентичные схемы (заголовки) или:

1. Если каждое из них имеет одно и то же множество имен атрибутов, т.е. они имеют одинаковую степень.

2. Если соответствующие атрибуты определены на одном и том же домене (соответственно, имеющие одинаковые имена в двух равных отношениях).

Объединение, пересечение и вычитание требуют от операндов совместимости по типу.

Объединение:

А union B; A U B

Пример:

R (A , B) S (A , B) R U S = Q (A , B)

a1 b1

a1 b2

a2 b1

a3 b1

a1 b1

a2 b2

a1 b1

a1 b2

a2 b1

a2 b2

a3 b1

Пересечение :

Aintersect B; A B

R (A , B) S (A , B) R S= Q (A , B)

a1 b1

a1 b2

a2 b1

a3 b1

a1 b1

a2 b2

a1 b1

A minus B; A-B

a1 b1

a1 b2

a2 b1

a3 b1

R (A , B) S (A , B) R - S = Q (A , B)

a1 b1

a2 b2

a1 b2

a2 b1

a3 b1

A times B

R

a1

a2

a3

a4

a1 b1

a1 b2

a2 b1

a2 b2

a3 b1

a3 b2

a4 b1

a4 b2

( A ) S ( B ) R times S= Q ( A , B)

b1

b2

Специальные реляционные операции:

1. Выборка

Пусть имеется отношение r(R), AєR;

a є dom(A)

r where A=a

Выбрать из отношения r все кортежи, удовлетворяющие условию А=a.

σ_A=a(r)

Пусть имеется таблица отношения расписаний автобуса:

номер	Пункт отправления	Пункт назначения	Время вылета	Время прибытия
201	Волгоград	Ростов	8,15	10,15
245	Волгоград	Самара	8,25	11,15
1304	Волгоград	Москва	19,25	21,10

r where номер 1304

r where пункт отправления Волгоград

r where пункт назначения Москва

Операция выборки обладает двумя свойствами:

1. Коммутативность

σ_A=a(σ_B=b(r))= σ_B=b(σ_B=b(r))

2. Дистрибутивностьотносительно трех классических операций

σ_A=a(r ﻻ s)= σ_A=a(r)ﻻ σ_A=a(s) ,где ﻻ = U, , -.

3. Проекция

В результате проекции мы получаем множество атрибутов

Определение: Пусть r(R) схема, а х- подмножество изR, тогда проекция на х изrобозначаетсяπ_x(r)

Свойства проекции:

1. Коммутатация с выборкой, если атрибуты для выбора находятся среди атрибутов множества, на которое осуществляется проекция

Если Aєx,x–подмножествоRиr(R), то

π_x(σ_A=a(r))= σ_A=a(π_x(r))

2. Дистрибутивность проекции с объединением

π_x(r Us)= π_x(r)U π_x(s)

пример:

r (A , B , C , D) s (A , B , C , D) x={ A,C}

a1 b1 c1 d1

a1 b2 c1 d2

a2 b1 c2 d1

a1 b2 c1 d2

a2 b2 c2 d2

a2 b1 c1 d1

a2 b1 c1 d2

r

a1 c1

a2 c2

U s = ( A, B, C, D) π_x(r U s )=( A, C) π_x(r )=(A, C) π_x(s )=(A, C)

a1 b2 c1 d2

a1 b1 c1 d1

a2 b1 c2 d1

a2 b2 c2 d2

a2 b1 c1 d1

a2 b1 c1 d2

a1 c1

a2 c2

a2 c1

a1 c1

a2 c2

a2 c1

a1 c1

a2 c2

a2 c1

π_x(r)U π_x(s)= (A, C) ч.т.д.

3. Соединение( не то же что и объединение!)

Рассмотрим два бинарных отношения

r(A,B)s(B,C)

rs– их соединение

Соединением отношений rиsназывают операцию, при которой эти отношения соединяют, используя в качестве признака соединения их общий атрибут или атрибуты

r s={(A, B, C)| (a, b) є r (b, c) є s}

пример: r (A, B) s (B, C) r s=(A, B, C)

a1 b1

a2 b2

a1 b2

a3 b1

b1 c2

b2 c1

b3 c1

a1 b1 c2

a2 b2 c1

a1 b2 c1

a3 b1 c2

Рассмотрим частные случаи соединения:

1. Схемы отношений rиsне пересекаются

Пример: r(R), s(S) R S= Ø

r s=r*s=r times s

c1 d1

c2 d1

c2 d2

r(A, B) s(C, D) r s=(A, B, C, D)

a1 b1 c1 d1

a1 b1 c2 d1

a1 b1 c2 d2

a2 b1 c1 d1

a2 b1 c2 d1

a2 b1 c2 d2

a1 b1

a2 b1

2. Схемы отношений rиsполностью совпадают

r(R), s(S) R- S= Ø

r s=r s

r(A, B) s(A, B) r s=(A, B)

a1 b1

a2 b1

a1 b2

a2 b1

a3 b1

a2 b1

Свойства операции соединения:

1. коммутативно и ассоциативно

(q r) s=q (r s)= q r s

2. При многократных соединениях кортежи могут быть соединены или нет

S1(S1),…,Sm(Sm); R=S1 U S2…U Sm;

S={S1,…,Sm}

Пусть t1,t2,,…,tm-последовательность кортежей, в которойtiєSi;iот 1 доm.

Кортежи t1,t2,,…,tmсоединены наS, если существует кортежtнаR, такой, что выполняетсяti=t(Si), т.е. кортежtявляется результатом соединенияt1,t2,,…,tmна множествеS.

Пример:

a1 b1

a1 b2

a2 b1

S1(A, B) S2(B, C) S3(A, C)

b1 c2

b2 c1

a1 c2

a2 c2

S1 S2 S3

R={A, B, C}

(a1 b1) (b1 c1) (a1 c2) (a1 b1 c2)

(a2b1) (b1c2) (a2c2) (a2b1c2)

Если некоторые кортежи, принадлежащие одному или нескольким соединяемым отношениям, не войдут в результат соединения, то заданное отношение не является полностью соединимым.

3. Для операций соединения и объединения справедливо следующее выражение:

(rUq)s= (rs)U(qs)

4. Операторы соединения проекции образуют дополнительные функции:

а) Пусть имеется отношениеr(R),s(S),q=rs(RUS)

Пусть

r^’=π_R(q)

Найдем связь r иr^’

r

a1 b1

a1 b2

b1 c1

a1 b1 c1

(A, B) s (B, C) q (A, B, C)

r^’=π_R(q)= (A, B)

a1 b1

т.е. r^’является подмножествомr.

Пример:

Найти (π_AB(s)-r) r

r

a3 b1

a1 b1 c1

a1 b2 c2

a2 b3 c1

a3 b1 c1

a1 b1

a1 b2

a2 b3

a3 b1

(A, B) s (A, B, C) π_AB(s)-r=(A, B) π_AB(s)=(A, B)

a1 b1

a1 b2

a2 b1

a2 b3

(π_AB(s)-r) r = Ø

б) r^’совпадет сr

пример:

r

a1 b1

a1 b2

b1 c1

b2 c2

(A, B) s (B, C) q= r s (A, B, C)

a1 b1 c1

a1 b2 c2

π_AB(q)=r^’(A, B)

a1 b1

a1 b2

в) q (R U S) q^’ = r s

r=π_R(q)

s=π_S(q) Если кортеж изq, то имеет место выражение

t(R) є r

t(S) є s t є q^’

q^’ q

Пример:

q (A, B, C) r= π_AB(q) (A, B)

a1 b1 c1

a1 b2 c2

a1 b1

a1 b2

q^’= r s (A, B, C) s= π_BC(q) (B, C)

a1 b1 c1

a1 b2 c2

b1 c1

b2 c2

q^’ =qт.е. можно сказать что отношениеqразложимо без потерь на схемыRиS.

5. Эквисоединения

Опр. Эквисоединением называется подмножество декартового произведения двух отношений, строки которого выбраны так, что они содержат совпадающие значения для сопоставимых атрибутов.

r(R), s(S)

Ai є R; Bi є S

dom (Ai)=dom (Bi), i є [1,m]

r[Ai=Bi,…,Am=Bm]s

при m=0r[ ]s=r*s

Пример:

Маршрут

Рейс	Пункт отправления	Пункт назначения
84	Волгоград	Москва
109	Пермь	Саратов
…..	…………….	…………….

Адрес

Пилот	Аэропорт
Иванов	Волгоград
Петров	Пермь
…….	……….

dom(пункт отправления)=dom(аэропорт)

Полеты

рейс	Пункт отправления	Пункт назначения	пилот	Аэропорт
84	Волгоград	Москва	Иванов	Волгоград
109	Пермь	Саратов	Петров	Пермь
…..	…………….	…………	………..	……….

Если в отношениях rиsсуществует один общий атрибут А, то естественное соединениеrиsэквивалентно операции эквисоединения.

r sr[A=A]s

6. Ө-соединение

Снимают ограничения на сравнение столбцов только по равенству значений при соединении.

r[A Ө B]s

r[A1>B1, A2=B2, A3<B3]s

Ө є {=,!=,.<,>,<=,>=}

Пример:

Есть отношение

Прибытие

рейс	Время вылета	Время прибытия
13	8,30	10,00
15	12,40	14,30

Отправление

рейс	Время вылета	Время прибытия
60	18,15	19,45
24	10,00	12,50

Прибытие [время прибытия <время вылета ] отправление

Транзит

Рейс_В	Время вылета	Время прибытия_В	Рейс_из	Время влета_из	Время прибытия
13	8,30	10,00	60	12,15	17,45

7. Переименование

δ_{А В}(r)

Атрибуты А и В должны иметь один и тот же домен

8. Деление

q=r/s r(R) s(S)

r/s- максимальное подмножествоqмножестваπ_R(r) , такое чтоqиsсодержится в отношенииr.

Пример:

Пусть имеется отношение

Право r

Пилот	Тип самолета
Иванов	707
---------	727
Петров	747
---------	707
Сидоров	727
----------	747
---------	Ил 86
Соловьев	747
---------	Ил 86

z={707,727}

r/z=q (Пилот)

Иванов

Петров

Деление можно записать через проекцию и соединение

r/s= π_R(r) – π_R((π_R(r) s)-r)