Примерный билет к модулю №1 по теме: «Волновая и квантовая оптика».

1. Волновые свойства света. Интерференция света. Когерентные волны. Разность хода лучей.

2. Дифракция света. Принцип Френеля. Метод зон Френеля.

3. Поляризация света. Двойное лучепреломление. Причина двойного лучепреломления.

4. Энергия кванта света равна 0,6 МэВ. Найти массу фотона и его импульс.

5. Вычислить радиусы первых пяти зон Френеля, если расстояние от источника света до волновой поверхности 1м., а длина волны 5,7 10^-7 м.

6. Найти, какое количество энергии с 1 см² в 1 с излучает черное тело , если известно, что максимальная спектральная плотность его энергетической светимости приходится на длину волны в 4840 А.

7. На стеклянную пластину положено выпуклой стороной плосковыпуклая линза с радиусом кривизны 1 м. Сверху линза освещается монохроматическим светом длинной волны 0,6 мкм. Определить расстояние между 4 и 9 темными кольцами ньютона в отраженном свете.

8. На дифракционную решетку падает нормально монохроматический свет (λ=0.5 мкм) при этом для максимума второго порядка получается угол отклонения максимума третьего порядка 15˚. Какова длина волны, для которой угол отклонения максимума третьего порядка 18˚.

9. На дифракционную решетку, содержащую 50 штрихов на 1 мм, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на спектр третьего порядка, чтобы видеть другой спектр третьего порядка трубу повернули на угол 10 ˚. Определить длину световой волны.

10. Абсолютно черное тело находится при температуре Т₁=2900˚К. В результате остывания этого тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости, изменилась на λ=9 мкм. До какой температуры Т₂ охладилось тело.

8. Волны де Бройля.

Длина волны де Бройля :

,

где р – импульс частицы.

Импульс частицы и его связь с кинетической энергией Т

а ) ;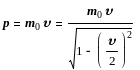

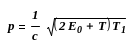б) ; ,

где m₀ – масса покоя частицы; m – релятивистская масса; υ – скорость части-цы; с –скорость света в вакууме; Е₀ – энергия покоя частицы (Е₀ = m₀ с²).

Пример решения задачи.

На узкую щель шириной а = 1 мкм направлен парал­лельный пучок электронов, имеющих скорость υ=3,65 • 10⁶ м/с. Учи­тывая волновые свойства электронов, определить расстояние х между двумя максимумами интенсивности первого порядка в дифракционной картине, полученной на экране, отстоящем на L = 10 см от щели.

Р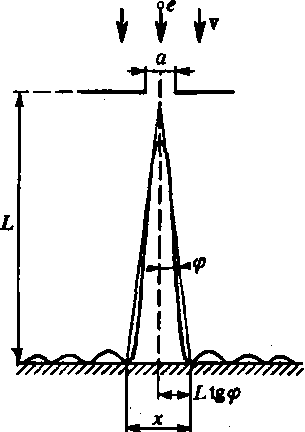 ешение. Согласно гипотезе де Бройля, длина волны λ, соответ­ствующая частице массой m, движущейся со скоростью υ, выражается формулой:

Дифракционный максимум при дифракции на одной щели наблюда­ется при условии

где к = 0, 1, 2, 3, ... — порядковый номер максимумов; a — ширина щели.

Для максимумов первого порядка (k=1) угол φ заведомо мал, поэтому sin φ= φ и, следовательно

А искомая величина х, как следует из рисунка

Подстановка в последнее равентсво длины волны Де Бройля по формуле дает

После вычисления по формуле получим: x=60мкм

Ответ: x=60мкм.