1.2 Конечный автомат

Рассмотрим некоторое устройство, приведенное на рисунке 1.1. Конечный автомат можно представить как устройство преобразования дискретной информации, имеющее конечное множество входных Х и выходных Y бинарных каналов и находящееся в каждый дискретный момент тактового времени t в одном из состояний конечного множества Z.

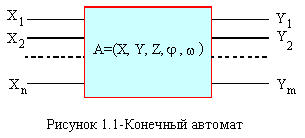
По входным каналам сообщений X в каждый текущий тактовый момент t в устройство поступает входной код (слово) из некоторого входного конечного множества X={x₁,x₂,…,х_n}, называемого входным алфавитом.

Указывается функция перехода (t) состояния Z(t) автомата в тактовый момент t_(i+1), в зависимости от входного кода и состояния устройства в текущий тактовый момент t, а также функция выхода (t), отражающая образование и значение (код) выходного слова конечного множества Y={y₁,y₂,…,y_m} выходного алфавита в такте t.

Такое устройство, которое характеризуется входным множеством сигналов X, выходным множеством сигналов Y, множеством внутренних состояний Z(t) и функциями переходов (t) и выходов (t), называется цифровым конечным автоматом.

Цифровой автомат без элементов памяти называют тривиальным автоматом, что характерно для комбинационных схем.

Итак, закон функционирования цифрового конечного автомата А можно представить математическим кортежем

А=Х,Y,Z,φ,, (1.1)

для которого в любом такте t_i выходящее слово является функцией

Y_i(t_i)=f_iX(t_i),Z(t_i),φ(t_i),(t_i). (1.2)

Существует два подхода при изучении, анализе и синтезе цифровых автоматов - макроподход и микроподход. При макроподходе интересуются внешним поведением автомата. Как он осуществляет переработку входной информации в выходную, в какой последовательности изменяются его состояния. При этом, не рассматривается внутреннее строение автомата, содержание его логических элементов, связей. На этом пути приходят к понятию абстрактного цифрового конечного автомата, который может быть задан с помощью набора входных сообщений, выходных логических функций, количества его состояний и переходов между ними, описывающих его поведение во времени и многомерном пространстве функций.

При микроподходе учитывается состав логических элементов, структура устройства, междуэлементные связи, логическая схема и ее математическое описание процесса функционирования при смене состояний автомата в различных последовательностях, его зависимость от входных булевых переменных. На этом пути приходят к понятию структурного конечного цифрового автомата. Структурный автомат может быть задан системой логических функций аналитического описания, табличным способом, графом автомата, граф-схемой алгоритма и другими способами. При этом задаются или выбираются ограничения по применению конечного множества логических интегральных схем (ИС) и схемой их взаимодействия между собой.

Обобщение конечного цифрового автомата получается путем объединения понятий абстрактного и структурного автоматов.

В соответствии с этим, вся теория автоматов разделена на теорию абстрактных автоматов и теорию структурных автоматов.

Теория абстрактных автоматов на уровне моделей изучает отношения между входной и выходной информацией и состояниями, которые отражают поведение автомата.

Основным содержанием теории структурных автоматов является изучение свойств отображений для разных композиций автомата из конечного множества микросхем относительно заданного класса логических функций и алгебр, анализ и синтез минимизированных схем.