
- •Часть 2
- •8.091501–«Компьютерные системы и сети» и
- •7.091503–«Специализированные компьютерные системы»
- •Содержание
- •Введение
- •1 Основные понятия и определения алгебры логики и цифрового конечного автомата
- •1.1 Основные определения алгебры логики
- •1.2 Конечный автомат
- •1.3 Основные логические операции
- •1.3.1 Операция отрицания
- •1.3.2 Операция логического умножения
- •1.3.3 Операция логического сложения
- •1.3.4 Операция эквиваленция
- •1.3.5 Операция импликация
- •1.3.6 Сумма по модулю 2
- •1.3.7 Штрих Шеффера
- •1.3.8 Стрелка Пирса
- •2 Зависимость состава функций от числа переменных
- •2.1 Состав функций при отсутствии входных переменных
- •2 .2 Функции одной переменной
- •2.3 Функции двух переменных
- •2.4 Действительные и фиктивные функции
- •2.5 Определение общего числа функций
- •3 Суперпозиция функций
- •3.1 Методы суперпозиции
- •3.2 Выражение одних элементарных функций через другие
- •4 Свойства законов и правила алгебры логики
- •4.1 Свойства операций конъюнкции, дизъюнкции и отрицания
- •4.2 Свойства суммы по модулю 2, импликации, функции Шеффера и Пирса
- •5.1.1 Представление лф в совершенной дизъюнктивной нормальной форме
- •5.1.2 Дизъюнктивная нормальная форма лф
- •5.1.3 Представление лф в совершенной конъюнктивной нормальной форме
- •5.2 Основные свойства и алгоритм получения сднф, скнф
- •5.2.1 Общие свойства сднф
- •5.2.2 Алгоритм записи сднф
- •5.2.3 Свойства скнф
- •5.2.4 Алгоритм записи скнф
- •5.3 Способы преобразования днф и кнф в сднф и скнф
- •6 Полные системы функций
- •6.1 Функционально полные базисы
- •6.2 Теорема Поста
- •7 Методы минимизации функций алгебры логики
- •7.1 Аналитический метод минимизации фл
- •7.2 Числовое и геометрическое представление фл
- •7.3 Минимизация фл с помощью комплекса кубов
- •7.3.1 Построение комплекса кубов и его минимального покрытия
- •7.3.2 Цена покрытия кубов
- •7.4 Метод неопределенных коэффициентов
- •8 Метод квайна-мак-класки
- •9 Метод минимизации фл с помощью карт карно
- •9.1 Правила минимизации по картам Карно
- •9.1.1 Соседние клетки
- •9.1.2 Правило объединения соседних клеток
- •9.1.3 Определение простых импликант
- •9 .2 Не полностью определенные логические функции в картах Карно
- •10 Анализ и структурный синтез цифровых автоматов
- •10.1 Задачи анализа и синтеза
- •10.2 Синтез элементов логических схем
- •10.3 Особенности схем логических элементов
- •10.3.1 Базовый логический элемент
- •10.3.2 Элемент с открытым коллектором
- •10.3.3 Элементы и - или – не и расширители
- •10.3.4 Трисабильные элементы
- •10.4 Временные параметры логических микросхем
- •10.5 Переходные процессы в логических схемах микросхем
- •11 Комбинационные схемы
- •11.1 Построение преобразователя кодов
- •11.2 Сумматоры
- •11.3 Временные логические функции
- •12 Способы задания цифровых конечных автоматов
- •12.1 Математические модели ца
- •12.2 Табличный способ задания ца
- •12.3 Задание цифрового автомата графом
- •12.4 Минимизация абстрактных автоматов
- •13 Методы структурного синтеза автоматов
- •13.1 Канонический метод синтеза автомата
- •13.1.1 Пример синтеза ца каноническим методом
- •13.2 Структурный синтез ца по методу графа автомата
- •13.3 Метод синтеза ца по граф–схеме алгоритма
- •13.4 Синтез автомата с жесткой логикой управления
- •13.4.1 Принцип работы микропрограммного автомата с жесткой логикой управления
- •13.4.2 Проектирование микропрограммного автомата с жесткой логикой управления
- •14 Язык задания поведения цу - vhdl и синтезатор leonardo
- •15 Программируемые логические матрицы
- •16 Схемы основных логических устройств
- •16.1 Элементы памяти последовательностных логических схем
- •16.1.1 Триггер
- •16.1.1.1 Асинхронный rs - триггер
- •16.1.1.2 Синхронный rs - триггер
- •16.1.2 Универсальный jk-триггер
- •16.2 Регистры
- •16.2.1 Параллельные и последовательные регистры
- •16.2.2 Реверсивный регистр сдвига
- •Список литературы
13.1.1 Пример синтеза ца каноническим методом
ЗАДАНИЕ. Синтезировать цифровой частичный автомат А, заданный таблицей переходов и выходов (таблица 13.1). Использовать канонический метод структурного синтеза автоматов. Принять: в качестве элементарных автоматов - логический расширенный базис Буля; в качестве элементов памяти - полный автомат Мура с двоичным алфавитом входных/выходных сигналов и состояний.
Таблица 13.1-Таблица переходов и выходов автомата А

РЕШЕНИЕ. Для перехода от абстрактного автомата к его структурному представлению, закодируем входные/выходные сигналы и состояния автомата Мили –А, и автомата Мура -П.
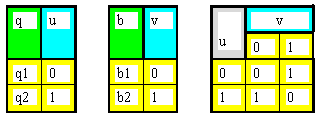
В заданном абстрактном автомате П каждый канал имеет два входных (q1, q2) и два выходных сигнала (b1,b2) двоичного алфавита. Поэтому, в структурном автомате П достаточно выбрать один входной u и один выходной v канал с двумя состояниями 0,1 каждый, т.е. обычный триггер с двумя состояниями. Результаты такого кодирования и отмеченная таблица переходов для структурного автомата П представлены таблицей 13.2.
Таблица 13.2-Коды входных/выходных сигналов и таблица переходов автомата
Автомат А имеет четыре состояния (см. таблицу 13.1), поэтому необходимы два элемента памяти П1 и П2. Три (X1, X2, X3) абстрактных входных и четыре (Y1, Y2, Y3, Y4) выходных сигнала могут быть представлены кодами двух входных и двух выходных каналов. Представим структурную схему автомата на рисунке 13.2.
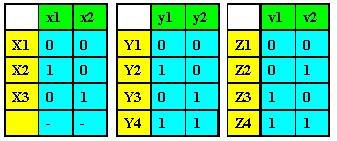
В таблице13.3 структурного автомата А представлены результаты кодирования входных, выходных сигналов и состояний заданных таблицей 13.1 для абстрактного автомата.

Таблица 13.3-Коды входных, выходных сигналов и состояний структурного автомата А
Теперь переходим к кодированию функций переходов и выходов структурного автомата А (см. таблицу 13.4), используя коды таблицы 13.3 и подставляя их в исходную таблицу13.1 заданного абстрактного автомата.
Исходя из математической модели канонического метода структурного синтеза автомата, строим систему логических функций автомата А (см. рисунок 13.2):
y1= y1(v1, v2, x1, x2);
y2= y2(v1, v2, x1, x2);
u1= u1(v1, v2, x1, x2);
u2= u2(v1, v2, x1, x2).
Таблица 13.4-Переходы и выходы структурного автомата А
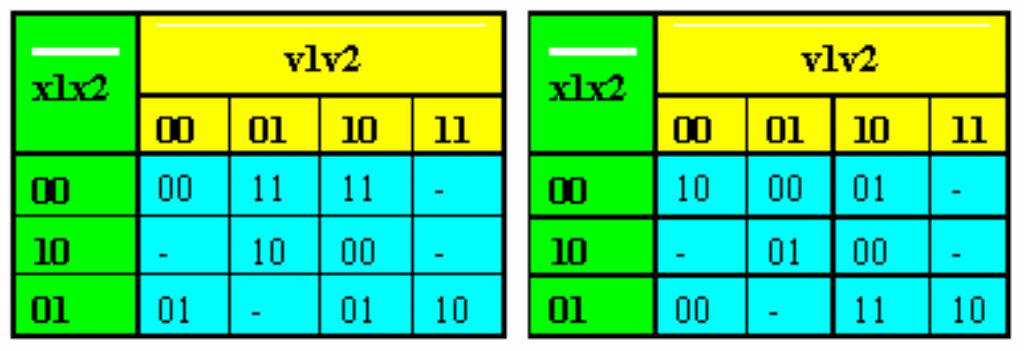
Функцию y2 получаем сразу непосредственно из таблицы 13.4 для выходов структурного автомата, как дизъюнкцию наборов переменных v1, v2, x1, x2 на которых эти функции принимают значение 1.Эти значения указаны в кодах на пересечении столбцов v1 v2 и строк x1, x2. Первая цифра соответствует значению функции y1, а вторая y2. Запишем функции:
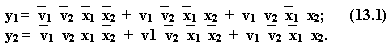
Для получения логических функций u1(v1, v2, x1, x2), u2(v1, v2, x1, x2), необходимо построить таблицу сигналов переключения u1, u2 элементов памяти П1 и П2. Для получения этой таблицы используем таблицу переходов структурного автомата (таблица 13.4). В этой таблице на пересечении столбцов и строк стоят значения переходов состояний элементов памяти П1, П2 (первая цифра - значение П1, вторая –П2), а в заглавиях столбцов v1 v2 стоят значения выходных сигналов П1, П2 или (отождествляя выход –состояние) значения состояний П1, П2, предшествующих переходу. Сравнивая эти состояния с состояниями переходов, определяем элементы памяти, которые переключаются (на их входы надо подавать сигнал 1) и которые не переключаются (на их входы надо подавать сигнал 0). Заполняя эти значения в аналогичную таблицу, получим таблицу сигналов u1, u2 переключения элементов памяти, представленную таблицей 13.5.
Непосредственно из этой таблицы составляем систему логических функций u1, u2 получая СДНФ для единичных наборов переменных v1, v2, x1, x2:

![]()
Логические функции систем уравнений 13.1, 13.2 являются математическим решением поставленной задачи структурного синтеза логической схемы цифрового автомата, каноническим методом.
По этим функциям строим логическую схему. Пример схемного решения логической функции u1 системы 13.2 представлен на рисунке13.3.
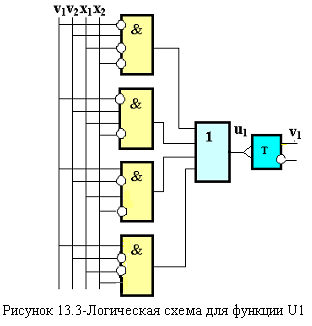
В качестве элемента памяти удобно выбрать триггер со счетным входом. Он имеет один вход, один прямой и один инверсный выход. Таблица переходов счетного триггера полностью совпадает с таблицей переходов автомата Мура П (см. таблицу 13.2).
