9 .2 Не полностью определенные логические функции в картах Карно
Не полностью определенные логические функции это функции, значение которых на некоторых наборах переменных несущественно (безразлично). Другими словами, это те функции, наборы переменных которых не используются при построении ЦА. Обычно их обозначают символом *. Например, при рассмотрении двоично-десятичных кодов используют десять функций от 0 до 9, а остальные шесть являются не затребованными и могут иметь различные значения, т.е. они не определены.
П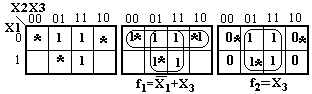
ри
минимизации не полностью определенной
функции ее можно доопределить
самостоятельно на свое усмотрение, для
этого вершины отмеченные символом *
изменяют, присваивая им значения 1 или
0, повышая, таким образом, эффективность
минимизации.
Рисунок 9.4 - Не полностью определенные ЛФ в картах Карно
Очень часто это упрощает процесс минимизации, так как добавление, например, единиц до существующих определенных наборов, позволяет включать в контур покрытия большее число единиц, снижая при этом число переменных в МДНФ. Доопределение функции при минимизации нулями также упрощает минимальную КНФ функции. Если функция имеет m неопределенных наборов переменных, то может быть 2m вариантов решения задачи ее доопределения. Желательно остановиться на варианте, который дает наибольший эффект при минимизации.
10 Анализ и структурный синтез цифровых автоматов
10.1 Задачи анализа и синтеза
Различные цифровые автоматы или их композиции на логическом уровне могут быть описаны с помощью логических функций.
Такое описание электронных схем позволяет абстрагироваться от физической сущности конкретных электронных элементов и осуществлять анализ и структурный синтез на логическом уровне, используя элементы математической логики. При этом оказывается, что для анализа совсем не обязательно иметь даже саму схему.
Для того чтобы получить логическую схему цифрового автомата, необходимо выбрать функциональный логический базис, имеющий микросхемное воплощение (например И, ИЛИ, НЕ). Т.е., определить логические операторы схемы, записать минимальные логические функции в данном базисе и нарисовать схему, отражающую связи логических операторов (логических элементов) между собой.
Задача анализа цифрового автомата с помощью аппарата алгебры логики может быть сформулирована как задача нахождения оптимальной логической функции, описывающей работу заданного автомата.
Однако, с точки зрения инженерного проектирования, чаще приходится решать задачу синтеза логических схем, включающую анализ.
Задача структурного синтеза состоит в том, что при заданных входных и выходных переменных цифрового автомата, его внешних связей с другими ЦА, его поведении во времени от конкретных входных кодов и состояний, необходимо проектировать систему логических функций и устройство, которое реализует эти функции. При этом могут быть наложены дополнительные ограничения, либо в виде базиса системы логических элементов, которые используются, либо в виде требований по количеству логических элементов, по их быстродействию, надежности и др.
Следовательно, в результате решения задачи синтеза возникает логическая и электрическая принципиальная схемы, воспроизводящие заданные математическим описанием функции.
Основные этапы структурного синтеза цифрового автомата:
-составление математического описания (системы логических уравнений) адекватного функционирования;
-анализ логических уравнений и получение минимальной формы для каждой из них в заданном базисе логических функций;
-построение логической схемы с применением логических элементов выбранного базиса;
-цифровое моделирование и испытание логической схемы;
-построение схемы электрической принципиальной с применением микросхем, с физическим воплощением заданного базиса логических функций.
Задача синтеза, как правило, имеет множество решений и зависит от вида математического описания логических функций, от проведенной минимизации, выбранного базиса системы логических функций, элементов микросхем и даже их использования и соединения.